
Мат.стат. и теория вероятностей / Лекции / Л6-ТВ
.pdf1
ЛЕКЦИЯ №6
СИСТЕМА ДВУХ СЛУЧАЙНЫХ ВЕЛИЧИН. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СИСТЕМЫ ДВУХ СЛУЧАЙНЫХ ВЕЛИЧИН
Под системой двух случайных величин будем понимать векторную
случайную величину, состоящую из двух случайных компонентов (величин)
X ,Y .
Пример непрерывной векторной случайной величины c двумя компонентами:
X ,Y рост, вес человека.
1. Ряд распределения системы двух случайных величин
Ряд распределения системы двух случайных величин есть таблица значений величин
P(x, y) P( X x,Y |
y) , |
(6.1) |
где выражение P( X x,Y y) понимается |
как вероятность |
совместного |
наступления событий: случайная величина |
X приняла значение x и |
|
случайная величина Y приняла значение y . |
|
|
Свойство ряда распределения P(xi , y j ) 1.
i j
2. Функция распределения системы двух случайных величин
Функцией распределения F (x, y) системы двух случайных величин
называется функция от двух аргументов, определяемая следующим выражением
F (x, y) P( X x,Y y) . |
(6.2) |
Неравенство, являющееся аргументом вероятности, понимается как вероятность совместного выполнения двух условий: случайная величина X примет значение строго меньше текущего x и случайная величина
значение строго меньше текущего y .
Свойства функции распределения F (x, y) :
1. Функция распределения системы двух случайных величин есть неубывающая функция.

2
2.F ( , y) F (x, ) F ( , ) 0 .
3.F ( , ) 1.
4. 0 F ( , y) 1, |
0 F (x, ) 1. |
|
3. Плотность распределения системы двух случайных величин |
||
Плотностью |
распределения |
f (x, y) системы двух случайных |
величин называется предел отношения вероятности попадания координат случайной точки ( X ,Y ) в бесконечно малый прямоугольник со сторонами
x, y к площади прямоугольника, то есть |
|
||||||||
|
f (x, y) lim |
P(x X x x, y Y y y) |
. |
(6.3) |
|||||
|
|
||||||||
|
|
x 0 |
|
|
x y |
|
|||
|
|
|
|
|
|
|
|
||
|
|
y 0 |
|
|
|
|
|
|
|
Свойства плотности распределения f (x, y) : |
|
||||||||
|
|
|
|
|
|
|
|
|
|
1. |
xy f (x, y) 0 . |
|
2. |
|
f (x, y)dxdy 1. |
|
|||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
3. |
P( X , Y ) f (x, y)dxdy , где , , , - константы. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 F (x, y) |
|
|
|
x |
y |
|
|
4. |
f (x, y) |
. |
5. |
|
f (x, y)dxdy . |
|
|||
x y |
F (x, y) |
|
|||||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
4. Частные распределения в системе двух случайных величин
Распределение одной случайной величины, входящей в систему двух случайных величин, называется частным распределением. Различают частный ряд, частную функцию распределения и частную плотность вероятности.
Частные ряды распределения Px (xi ) , Py ( y j ) для дискретной случайной величины X со значениями xi (i 1, m ) и дискретной случайной величины Y со значениями y j ( j 1, n) получают по формулам
n |
|
|
m |
|
Px (xi ) P(xi , y j ) ; |
Py ( y j ) P(xi , y j ) . |
(6.4) |
||
j 1 |
|
|
i 1 |
|
Частные функции |
распределения |
Fx (x) , Fy ( y) |
получают из |
|
следующих выражений |
Fx (x) F (x, ) , |
Fy ( y) F( , y) . |
||
3
Для дискретной случайной величины с известным рядом распределения
k 1 |
n |
|
|
m |
l 1 |
|
||
Fx (xk ) P(xi , y j ) , |
Fy ( yl ) P(xi , y j ) . |
(6.5) |
||||||
i 1 j 1 |
|
|
i 1 j 1 |
|
||||
Для непрерывной случайной величины с известным рядом |
||||||||
распределения |
|
|
|
|
|
|
|
|
x |
|
|
|
y |
|
|
|
|
Fx (x) |
f (x, y)dy dx , |
Fy ( y) |
|
|
f (x, y)dx dy . |
(6.6) |
||
|
|
|
|
|
|
|
||
Частные плотности распределения fx (x) , f y ( y) получают |
по |
|||||||
формулам |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
fx (x) |
|
f (x, y)dy , |
f y ( y) |
|
f (x, y)dx . |
(6.7) |
||
|
|
|||||||
|
|
|
|
|
|
|
|
|
5. Условные распределения в системе двух случайных величин |
|
|||||||
Распределение |
случайных |
величин, |
|
рассматриваемое |
в |
|||
предположении, что другие величины, входящие в систему, приняли определенное значение называется условным.
Условные |
ряды |
|
распределения |
P(x / y) , |
P( y / x) системы |
|||||||||||||
дискретных случайных величин X ,Y определяются по формулам |
|
|||||||||||||||||
P(x / y) |
P(x, y) |
, |
|
P( y / x) |
P(x, y) |
. |
|
|
(6.8) |
|||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
Py ( y) |
|
|
|
|
Px (x) |
|
|
|||||||
Условные |
функции распределения |
F (x / y), |
F ( y / x) |
системы |
||||||||||||||
дискретных случайных величин X ,Y определяются по формулам |
|
|||||||||||||||||
F (x / y) |
F (x, y) |
, |
|
F ( y / x) |
F (x, y) |
|
. |
(6.9) |
||||||||||
|
|
Fx (x) |
||||||||||||||||
|
|
|
Fy ( y) |
|
|
|
|
|
|
|||||||||
Условные |
плотности распределения |
|
|
f (x / y) , |
f ( y / x) системы |
|||||||||||||
непрерывных случайных величин X ,Y определяются по формулам |
||||||||||||||||||
f (x / y) |
|
f (x, y) |
, |
f ( y / x) |
|
f (x, y) |
. |
|
(6.10) |
|||||||||
|
|
|
|
|
||||||||||||||
|
|
|
|
|
f y ( y) |
|
|
|
|
fx (x) |
|
|
||||||
Для независимых дискретных случайных величин X и Y
|
4 |
|
P(x / y) Px (x) , |
F (x / y) Fx (x) , |
(6.11) |
P( y / x) Py ( y) , |
F( y / x) Fy ( y) . |
(6.12) |
Для независимых непрерывных случайных величин X и Y
f (x / y) fx (x) , |
f ( y / x) f y ( y) . |
(6.13) |
Задача 6.1. Имеется 6 одинаковых деталей, из которых 2 бракованные. Проводится безошибочная экспертиза качества деталей, в результате которой определяется число проверенных деталей X до момента обнаружения первой бракованной и число проверенных деталей Y от момента обнаружения первой бракованной до момента обнаружения второй бракованной. Требуется построить:
1.Ряд распределения P(x, y)системы случайных величин X ,Y .
2.Частные ряды распределения Px (x) , Py ( y) системы случайных величин
X ,Y .
3.Функцию распределения F (x, y) системы случайных величин X ,Y .
4.Частные функции распределения Fx (x) , Fy ( y) системы случайных
величин X ,Y .
5. Условные ряды распределения P(x / y) , P( y / x) системы случайных величин X ,Y .
6. Установить являются ли зависимыми случайные величины X и Y .
Решение:
1. Перед построением ряда распределения системы случайных величинX ,Y , определим мощности множеств значений данных величин.
Очевидно, что случайная величина X может принять значения 1, 2, 3, 4, 5
( m 5), а случайная величина Y также может принять значения 1, 2, 3, 4, 5
(n 5) .
Тогда P( X 1,Y 1) P(1,1) |
|
2 |
1 |
|
|
1 |
; |
|
|
|
|||||||||
6 5 |
15 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
P( X 1,Y 2) P(1, 2) |
|
2 4 1 |
|
|
1 |
|
; |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
6 5 4 |
|
15 |
|
|||||||||||||||
|
|
|
|
|
|
|
|||||||||||||
P( X 1,Y 3) P(1,3) |
2 4 3 1 |
|
|
1 |
|
; |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
6 5 4 3 |
|
15 |
|||||||||||||||||
|
|
|
|
|
|||||||||||||||
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
|
|
||

5
P( X 5,Y 1) P(5,1) 64 53 24 131 1 151 .
Ряд распределения P(x, y)представлен в таблице 6.1.
Таблица 6.1
|
|
|
|
|
|
y1 1 |
|
|
y2 2 |
|
y3 3 |
y4 4 |
|
y5 5 |
|
|
|
|||||||||
|
|
x1 1 |
|
|
|
1/15 |
|
|
1/15 |
1/15 |
|
|
1/15 |
|
|
1/15 |
|
|
|
|||||||
|
|
x2 2 |
|
|
|
1/15 |
|
|
1/15 |
1/15 |
|
|
1/15 |
|
|
0 |
|
|
|
|
||||||
|
|
x3 3 |
|
|
|
1/15 |
|
|
1/15 |
1/15 |
|
|
0 |
|
|
0 |
|
|
|
|
||||||
|
|
x4 4 |
|
|
|
1/15 |
|
|
1/15 |
|
|
0 |
|
|
0 |
|
|
0 |
|
|
|
|
||||
|
|
x5 5 |
|
|
|
1/15 |
|
|
0 |
|
|
0 |
|
|
0 |
|
|
0 |
|
|
|
|
||||
|
|
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отметим, что P(xi , y j ) 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
i 1 |
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2. |
Частные ряды Px (x) , Py ( y) найдем по формулам |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
||||
|
|
|
i Px (xi ) P(xi , y j ) ; |
j Py ( y j ) P(xi , y j ) . |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
||||
Ряды Px (x) |
Py ( y) представлены в таблицах 6.2-6.3. |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 6.2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
xi |
|
|
|
|
x1 1 |
|
x2 2 |
|
x3 3 |
|
x4 4 |
x5 5 |
|
|
|
|
|
||||||
|
|
|
Px (x) |
|
5/15 |
|
4/15 |
|
|
3/15 |
|
|
2/15 |
|
1/15 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 6.3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
y j |
|
|
|
|
y1 1 |
|
|
y2 2 |
|
y3 3 |
|
y4 4 |
|
y5 5 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Py ( y) |
|
|
5/15 |
|
|
4/15 |
3/15 |
|
|
2/15 |
|
1/15 |
|
|
|
|
|
||||||
3. |
Функцию |
|
|
распределения |
|
|
F (x, y) найдем |
из |
условия |
|||||||||||||||||
|
F (x, y) P( X x,Y y) по |
формуле |
суммирования |
вероятностей |
||||||||||||||||||||||
|
событий |
удовлетворяющих |
условию |
( X xi ,Y y j ), то есть |
||||||||||||||||||||||
|
|
|
k 1 l 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Fx (xk , yl ) P(xi , y j ) см. таблицу 6.4. |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
i 1 |
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
6
|
|
|
|
|
|
|
Таблица 6.4 |
|
|
|
|
|
|
|
|
|
|
F( x, y ) |
y1 1 |
y2 2 |
y3 3 |
y4 4 |
y5 5 |
y6 6 |
|
|
x1 1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
x2 2 |
0 |
1/15 |
2/15 |
3/15 |
4/15 |
5/15 |
|
|
x3 |
3 |
0 |
2/15 |
4/15 |
6/15 |
8/15 |
9/15 |
|
x4 |
4 |
0 |
3/15 |
6/15 |
9/15 |
11/15 |
12/15 |
|
x5 |
5 |
0 |
4/15 |
8/15 |
11/15 |
13/15 |
14/15 |
|
x6 |
6 |
0 |
5/15 |
9/15 |
12/15 |
14/15 |
15/15 |
|
4. Частные функции распределения Fx (x) , Fy ( y) системы случайных величин X ,Y получим, воспользовавшись формулами
|
|
|
k 1 |
5 |
|
|
|
|
|
|
|
|
Fx (xk ) P(xi , y j ) , |
k 1,2,3,4,5,6 ; |
|
|
|||||
|
|
|
i 1 |
j 1 |
|
|
|
|
|
|
|
|
5 |
l 1 |
|
|
|
|
|
||
|
|
Fy ( yl ) P(xi , y j ) , |
l 1,2,3,4,5,6 . |
|
|
|||||
|
|
|
i 1 |
j 1 |
|
|
|
|
|
|
Функции распределения Fx (x) , Fy ( y) представлены в таблицах 6.5-6.6 |
||||||||||
|
|
|
|
|
|
|
|
|
Таблица 6.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
xi |
|
x1 1 |
|
x2 2 |
x3 3 |
x4 4 |
x5 5 |
x6 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Fx ( x ) |
|
0 |
|
5/15 |
9/15 |
12/15 |
14/15 |
15/15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 6.6 |
|
|
|
|
|
|
|
|
|
|
||
|
y j |
|
y1 1 |
|
y2 2 |
y3 3 |
y4 4 |
y5 5 |
y6 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Fy ( y ) |
|
0 |
|
5/15 |
9/15 |
12/15 |
14/15 |
15/15 |
|
|
|
|
|
|
|
|
|
|
|
|
5. Условные ряды распределения P(x / y) , P( y / x) системы случайных величин X ,Y получим, воспользовавшись формулами
|
|
|
7 |
|
|
P(x / y) |
P(x, y) |
, |
P( y / x) |
P(x, y) |
. |
|
|
||||
|
Py ( y) |
|
|
Px (x) |
|
Условные ряды P(x / y) P( y / x) представлены в таблицах 6.7-6.8 .
Таблица 6.7
|
|
x1 1 |
x2 2 |
x3 3 |
x4 4 |
x5 5 |
P( xi / y1 |
) |
1/5 |
1/5 |
1/5 |
1/5 |
1/5 |
P( xi / y2 |
) |
1/4 |
1/4 |
1/4 |
1/4 |
0 |
P( xi / y3 |
) |
1/3 |
1/3 |
1/3 |
0 |
0 |
P( xi / y4 |
) |
1/2 |
1/2 |
0 |
0 |
0 |
P( xi / y5 ) |
1 |
0 |
0 |
0 |
0 |
|
Таблица 6.8
|
|
y1 1 |
y2 2 |
y3 3 |
y4 4 |
y5 5 |
P( yi / x1 |
) |
1/5 |
1/5 |
1/5 |
1/5 |
1/5 |
P( yi / x2 |
) |
1/4 |
1/4 |
1/4 |
1/4 |
0 |
P( yi / x3 ) |
1/3 |
1/3 |
1/3 |
0 |
0 |
|
P( yi / x4 |
) |
1/2 |
1/2 |
0 |
0 |
0 |
P( yi / x5 ) |
1 |
0 |
0 |
0 |
0 |
|
Для установления зависимости (независимости) величин сравним любую из строк условного ряда распределения P( y / x) с частным
рядом распределения Py ( y) . |
Для сравнения представим в таблице первую |
|||||||||
строку P( yi |
/ x1 ) и закон Py ( y) |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y1 1 |
|
y2 2 |
|
y3 3 |
y4 4 |
|
y5 5 |
|
|
Py ( y ) |
5/15 |
|
4/15 |
|
3/15 |
2/15 |
|
1/15 |
|
|
P( yi / x1 ) |
3/15 |
|
3/15 |
|
3/15 |
3/15 |
|
3/15 |
|
Если бы все значения |
|
Py ( y) совпали со всеми соответствующими |
||||||||
значениями |
P( y / x) можно было бы |
говорить о |
независимости величин |
|||||||
X ,Y . Но в данном случае вероятность реализации случайной величины Y
8
зависит от того, какое значение приняла случайная величина X , и, следовательно, случайные величины X ,Y являются зависимыми.
Задача 6.2. Система случайных величин X ,Y имеет плотность распределения, заданную следующим выражением
|
|
|
|
|
|
|
|
|
|
|
|
1 / 50, |
x |
|
5,10 |
|
и |
y |
10,20 |
|
; |
||
f (x, y) |
0, |
x |
|
5,10 |
|
|
|
|
|
. |
|
|
|
|
|||||||||
|
|
|
или y |
10,20 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
Определить функцию |
распределения |
данной |
|
системы случайных |
|||||||
величин, частные и условные функции распределения в области определения |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
аргумента (x |
|
5,10 |
|
и y |
10, 20 )и установить зависимы или не зависимы |
||||||||||||||||||||||||||||||||
случайные величины X ,Y . |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
x |
|
y |
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
x |
|
|
y |
|
|
|
1 |
x |
||||||||
F (x, y) |
|
|
|
|
|
|
dxdy |
|
|
|
dx dy |
|
|
( y 10)dx |
|||||||||||||||||||||||
50 |
50 |
50 |
|||||||||||||||||||||||||||||||||||
|
|
|
|
5 10 |
|
|
|
|
|
|
|
5 |
|
|
10 |
|
|
|
|
5 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
(x 5)( y 10) |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
50 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
F (x) |
x 20 1 |
|
dxdy |
|
|
x 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
x |
|
|
|
50 |
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
5 10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
F ( y) |
10 |
|
y |
|
|
1 |
|
dxdy |
|
y 10 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
50 |
|
10 |
|
|
; |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
F (x / y) |
(x 5)( y 10) |
: |
|
|
y 10 |
|
x 5 |
; |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
50 |
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
5 |
|
|
||||||
F ( y / x) |
(x 5)( y 10) |
: |
x 5 |
|
y 10 |
. |
|||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
50 |
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
10 |
|
|
||||||
|
|
Так как |
F (x / y) F (x) и |
F ( y / x) F ( y) полагаем, что случайные |
|||||||||||||||||||||||||||||||||
величины X ,Y независимы. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
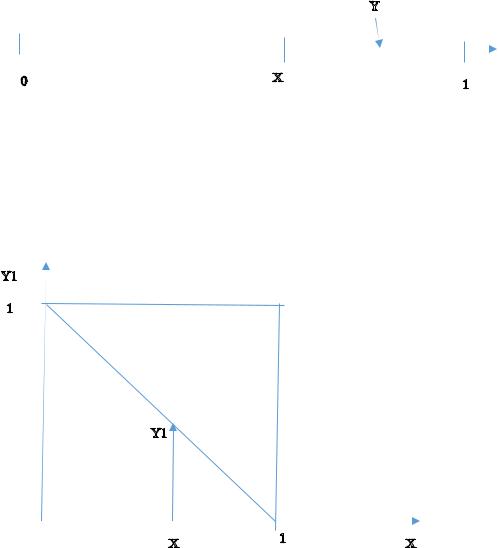
9
Задача 6.3. На отрезок длины L 1 бросаются две точки X и Y . Так, |
|||||
|
|
|
|
|
1 |
что X R |
0,1 , а Y R |
|
X ,1 , т е. 0 |
X Y 1. Найти |
P( X Y ) , где |
Y1 Y X .
Решение: |
|
|
|
|
Так как f (x) 1 / 1; |
f ( y1 / x) 1 / (1 x) , то – |
геометрически |
||
область для совместной плотности f (x, y1 ) – треугольник, |
ограниченный |
|||
сверху линией Y1 1 X . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При |
|
|
чем |
|
f (x, y1 ) const , |
|
|
|
так |
как |
|||||||||||
f (x, y1 ) f (x) f y1 |
/ x 1 |
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
1 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Тогда имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
1/2 |
|
x |
|
1 |
|
|
1 |
1 x |
|
|
1 |
|
||
P Y1 |
X |
|
f (x, y1 )dxdy1 |
|
|
dx |
|
1 |
dy1 |
|
|
dx |
|
1 |
|
dy1 |
||||||||
1 x |
|
x |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|||||||||
|
|
|
|
Doxy1 |
|
|
|
|
0 |
|
|
0 |
|
|
|
1/2 |
|
0 |
|
|
|
|
||
|
1/2 |
1 x |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
x |
dx |
|
dx ln 0,5 0,69. |
|
|
|
|
|
|
|
|
|
|
|
|||||||
0 |
|
|
1/2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
