Добавил:

Chupapi_Munyanya Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МЭИ»

Предмет:

Высшая математика

Файл:

Л4-ТВ

.pdf

Скачиваний:

Добавлен:

16.05.2024

Размер:

453.96 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

ЛЕКЦИЯ №4

ЗАКОНЫ РАСПРЕДЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН

1. Классификация случайных величин. Понятие закона распределения

Случайной называется такая величина, которая в результате опыта (эксперимента) может принять то или иное значение, при чем заранее неизвестно какое именно.

Случайные величины обозначают большими буквами X ,Y , Z..., а

возможные (конкретные) значения случайных величин - малыми буквами, соответственно x, y, z...

Пример 4.1.

X x - случайная величина X приняла значение x .

Случайные величины (СВ) классифицируют по следующим позициям:

1.Дискретные.

2.Непрерывные.

3.Смешанные.

Дискретной случайной величиной (ДСВ) называют величину, возможные значения которой принимают конечное или бесконечное, но счетное число значений.

Примеры. Число шаров фиксированного цвета в возвратной выборке объема m из конечного набора в n шаров разных цветов (ДСВ конечного типа). Число видимых звезд на небе в конкретное время суток (ДСВ бесконечного, но счетного типа).

Непрерывной случайной величиной (НСВ) называют величину, возможные значения которой непрерывно заполняют некоторый диапазон возможных значений.

Примеры. Температура окружающей среды, атмосферное давление, вес и рост человека и.т.д.

Случайные величины также подразделяются на скалярные и векторные. Скалярная величина может быть представлена только единственным значением. Векторная величина состоит из системы случайных величин.

Стаценко И.В. Лекция 4. Теория вероятностей и математическая статистика

Под законом распределения СВ понимают всякое соотношение, устанавливающее взаимосвязь между возможными значениями (диапазонами значений) СВ и вероятностями их реализации.

Основными законами распределения СВ являются:

1.Ряд распределения.

2.Функция распределения.

3.Функция плотности вероятности.

2. Ряд распределения дискретной случайной величины

Ряд распределения вводится	только для	дискретной случайной
величины.
Под рядом распределения -	p(x) P X x		ДСВ ( X -имя СВ)
понимают таблицу, в которой возможным значениям			x1, x2 ,..., xn СВ X
ставятся в соответствие вероятности их реализации		p x1 , p x2 ,..., p xn .
Основное свойство ряда распределения:
p xi 1.			(4.1)
i

Пример 4.2. Монетка бросается на идеальную горизонтальную поверхность 3 раза. Пусть X - число появлений герба в данном эксперименте. Построить ряд распределения.

Решение.

xi	0	1	2	3
p xi	0,125	0,375	0,375	0,125

Стаценко И.В. Лекция 4. Теория вероятностей и математическая статистика

3. Функция распределения случайной величины

Функция распределения, в отличие от ряда распределения, является универсальной характеристикой случайной величины, так как может быть задана для случайных величин дискретного и непрерывного типа.

Под функцией распределения от аргумента	x случайной величины
X понимают зависимость F (x) , задаваемую правилом
F (x) P( X x) .	(4.2)
Таким образом, функция распределения F (x)	случайной величины X
есть вероятность того, что случайная величина X примет значения строго
меньше некоторого текущего (фиксированного) значения x .

Пример 4.3. В ящике находится 10 деталей, из которых три бракованные. Последовательно и безвозвратно извлекают четыре детали. Построить ряд распределения и функцию распределения случайной величины X - числа извлеченных бракованных деталей в данной выборке.

Решение:

Очевидно, что случайная величина X имеет дискретное множество значений - X 0,1, 2,3, .

Ряд распределения данной случайной величины имеет вид:

						xi						0				1		2			3
						P( xi		)				0,167				0,5		0,3		0,0333
P(0)				7 6 5 4							1		0,167 ;

			10 9 8 7							6
			10 9 8 7							6
P(1)			3 7 6 5							7 3 6 5						7 6 3 5		7 6 5 3	0,5;
P(1)																			0,5;
			10 9 8 7					10 9 8 7							10 9 8 7		10 9 8 7
P(2)				3 2 7 6						7 3 2 6						7 6 3 2		3 7 2 6

			10 9 8 7							10 9 8 7						10 9 8 7		10 9 8 7
			10 9 8 7							10 9 8 7						10 9 8 7		10 9 8 7
	3	7	6		2		7	3	6			2		0,3;
														0,3;
10 9 8 7						10 9 8 7
P(3)				3 2 1 7						7 3 2 1						3 7 2 1		3 2 7 1		1	0,0333.

			10 9 8 7							10 9 8 7						10 9 8 7		10 9 8 7		30
			10 9 8 7							10 9 8 7						10 9 8 7		10 9 8 7		30

Стаценко И.В. Лекция 4. Теория вероятностей и математическая статистика

Функцию распределения данной случайной величины можно представить в табличном виде следующим образом:


xi	0	1	2	3	x 3
F(xi )	0	0,167	0,667	0,967	1

Где F (0) P( X 0) 0;

F (1) P( X 1) P(0) 0 ;

F (2) P( X 2) P(0) P(1) 0,167 ;

F (3) P( X 3) P(0) P(1) P(2) 0,667 ;

F ( X 3) P( X 3) P(0) P(1) P(2) P(3) 1.

Свойства функции распределения случайной величины.

1.Функция распределения случайной величины является неубывающей функцией.

2.lim F (x) 0 .

3.	lim F (x) 1.
	x
4.	Вероятность того, что случайная величина			X окажется в интервале

	значений	,	определяется		равенством
	P( X ) F ( ) F ( ) .
		4.Функция плотности вероятности
	Плотность вероятности является характеристикой случайной
величины непрерывного типа.
	Функция f (x)	плотности распределения		случайной величины X в

точке x есть предел отношения вероятности попадания случайной величины на бесконечно малый участок к длине данного участка, т.е.

f (x) lim	P(x X x x)	lim	F (x x) F (x)	F (x) . (4.3)
	x		x
x 0		x 0

Свойства функции плотности вероятности случайной величины X .

1. P( X ) f (x)dx F ( ) F ( ) ,

где ,b - константы.

Стаценко И.В. Лекция 4. Теория вероятностей и математическая статистика

2. x f (x) 0 - плотность распределения является неотрицательной функцией.

3. f (x) 1.

4. f (x) F (x) .

5. F (x) x	f (x)dx .

Пример 4.4. Время ожидания t		(мин) очередного вызова скорой
помощи на станции скорой помощи		имеет плотность	вероятности,
определяемую	следующей функцией	f (t) 0,1e 0,1t .	Определить

вероятность того, что вызов придет не более чем, через 15 мин.

Решение:

Необходимо найти вероятность события A , заключающегося в том, что время ожидания будет находиться в диапазоне 0 t 15 , т.е.

P( A) P(0 t 15) 0,1e 0,1t dt e 0,1t 150 e 1,5 1 0,777.

0
Пример 4.5. Определить			недостающий параметр k функции
плотности вероятности случайной величины, имеющей следующий вид:
f (x) 0,			для x 1,
	- x	,	для	1 x 2,
f (x) ke		,	для	1 x 2,
f (x) 0,			для	x 2.

Решение: Используя свойство 3 функции плотности вероятности
случайной величины, получим
2

ke x dx 1 ke x			2 1 ke 2 ke 1 1 k 4,3.
			1
1

Стаценко И.В. Лекция 4. Теория вероятностей и математическая статистика

5.Модели некоторых непрерывных распределений случайной величины

Рассмотрим наиболее распространенные в практике модели распределений непрерывной случайной величины.

5.1. Равномерное распределение

Непрерывная

случайная величина

имеет равномерное

распределение на отрезке a,b , если на этом отрезке плотность распределения

постоянна, а вне его равна нулю

f (x)

c const,

a x

x a

и x b.

Постоянную

c найдем,

используя

известное

свойство плотности

распределения

cdx 1

c(b a) 1

b a

Основные характеристики равномерно распределенной случайной

величины определяются по формулам

b a

- центр распределения;

среднее

квадратическое отклонение СВ,

a b

имеющей равномерное распределение, от центра распределения.

Равномерному распределению подчинено, как правило, время ожидания события, имеющего некоторую регулярную периодичность наступления.

Пример 4.6. На некоторой станции поезда метрополитена следуют с равномерным интервалом времени 2 минуты. Определить среднее время ожидания поезда, среднее квадратическое отклонение времени ожидания, а также вероятность того, что время ожидания не превзойдет 1,5 мин.

Решение:

Полагаем, что случайная величина T - время прибытия поезда имеет равномерное распределение на отрезке 0, 2 , тогда

m	2	1мин;
	2		t	0,333 0,58 мин.
				0,333 0,58 мин.
t	2
	2

Стаценко И.В. Лекция 4. Теория вероятностей и математическая статистика

Вероятность события T 1,5 найдем, воспользовавшись известным

свойством плотности вероятности P(a X ) f (x)dx .


1,5	dt	1,5
P(T 1,5)			0,75 .
P(T 1,5)	2	2	0,75 .
0	2	2
0

5.2.Показательное распределение

Плотность вероятности случайной величины X , имеющей показательное распределение, задается следующим образом:

e x ,		0,	x 0.
f (x)	0,	x 0.

Основные числовые характеристики случайной величины, имеющей показательное распределение, определяются по формулам

mx	1	;	x	1	.

Показательному распределению подчинено, как правило, время работы до момента отказа различных технических систем и устройств.

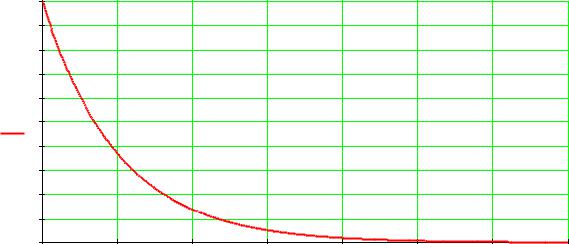
На рис 4.1. представлена функция плотности вероятности показательного распределения для =1 .

0.9

0.8

0.7

0.6

f(x) 0.5

0.4

0.3

0.2

0.1

Рис. 4.1.

Стаценко И.В. Лекция 4. Теория вероятностей и математическая статистика

Пример 4.7. Электронасос подачи воды в системе водоснабжения в среднем работает до момента отказа 25000 часов. Определить вероятность того, что а) данный электронасос проработает не менее 25000 часов; б) данный электронасос проработает менее 30000 час

Решение: Полагаем, что случайная величина T - время работы электронасоса до момента отказа имеет показательное распределение и известно математическое ожидание данной величины, т. е. mt 25000

1 / 25000.

Далее используем свойства плотности вероятности случайной величины

P(T t) 1 F (t) 1 t				f (t)dt ;		P(T t) t				f (t)dt .
			0						0
Определим вероятность того, что насос проработает не менее 25000
часов
	25000		t				t
	25000		25000				t
		e						25000
P(T 25000) 1		e			dt 1 ( e		25000 )		0,37.
P(T 25000) 1					dt 1 ( e		25000 )		0,37.
		25000						0
		25000
	0

Определим вероятность того, что насос проработает менее 30000 часов

30000

P(T 30000) 1 e 25000 0,7 .

5.3. Нормальное распределение

Нормальное распределение - наиболее часто встречающееся распределение случайных величин в природе. Распространенность нормального распределения объясняется тем, что оно является предельным распределением, к которому приближаются другие распределения при условиях, довольно часто встречающихся на практике.

В фундаментальном курсе теории вероятностей А.М.Ляпуновым сформулирована, так называемая, центральная предельная теорема:

распределение суммы достаточно большого числа независимых или слабо зависимых случайных величин с примерно одинаковыми дисперсиями и произвольными распределениями приближается к нормальному распределению.

Обоснование нормального распределения исторически связывают с именем К.Гаусса, поэтому его часто называют также распределением Гаусса.

Плотность нормального закона распределения может быть представлена в следующем виде

		1			( x mx )2
					2
					2
f (x)				e	2 x	,
	x
	x		2

Стаценко И.В. Лекция 4. Теория вероятностей и математическая статистика

					9
где	mx	и x -	математическое		ожидание	и	среднее	квадратическое
отклонение случайной величины X ,					имеющей нормальное распределение.
Величины		mx и x	также	называют параметрами нормального закона
распределения.
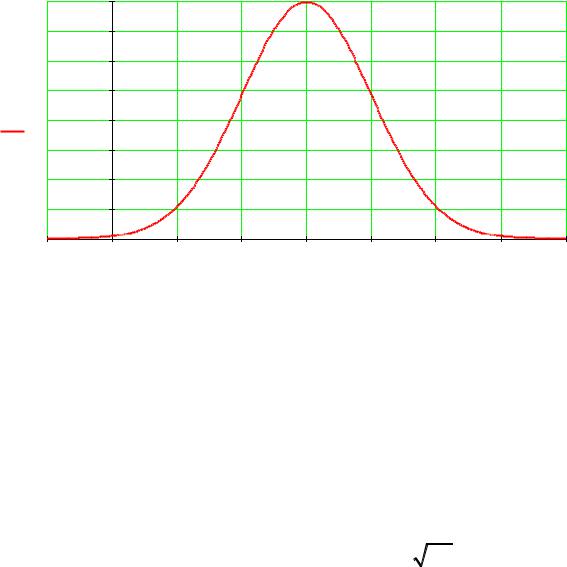
	На рис 4.2. представлена функция плотности вероятности
нормального распределения для mx =3 и x 1.
	0.4
	0.35
	0.3
	0.25
f(x)	0.2
	0.15
	0.1
	0.05
1	0	1	2	3	4	5	6	7
				x

Рис. 4.2.

Свойства нормального распределения:

1.Нормальное распределение полностью характеризуется (задается) двумя параметрами - математическим ожиданием и дисперсией (средним квадратическим отклонением).

2.Нормальное распределение случайной величины X является

	симметричным относительно mх .
3.	Максимум		плотности	вероятности				распределения отвечает
	абсциссе равной mx .
			f (mx ) fmax		(x)		1		.


						x		2
						x		2
4.	lim f (x) lim		f (x) 0 .
	x	x
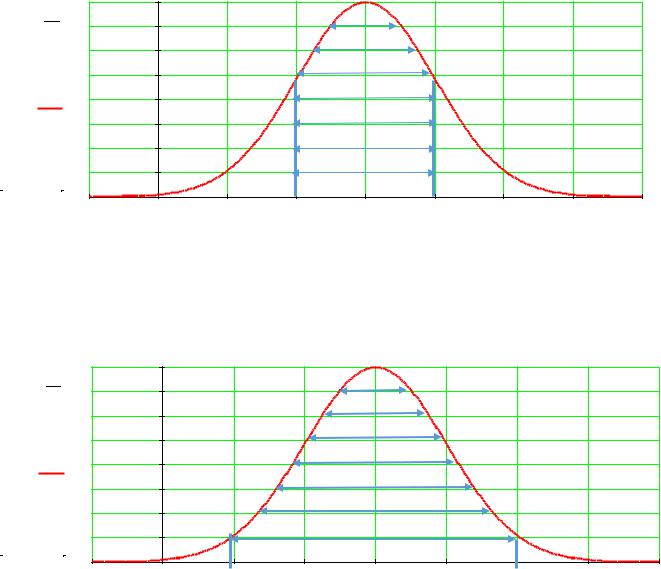
5.	На отрезке mx x X mx			x	случайная величина X распределяется
с вероятностью P(S1 ) 0,683. См. рис. 4.3.

Стаценко И.В. Лекция 4. Теория вероятностей и математическая статистика

		0.4
4
10		0.35
10
		0.3
		0.25
f ( x)		0.2
		0.15
		0.1
1.338 10 4		0.05
1.338 10 4
	1	0		1	2	3	4	5	6	7
	1					x				7
		Рис. 4.3.
6.	На	отрезке	mx	2 x	X mx	2 x	случайная		величина	X
	распределяется с вероятностью P(S2 ) 0,954. См. рис. 4.3.
		0.4
4
10		0.35
10
		0.3
		0.25
f ( x)		0.2
		0.15
		0.1
1.338 10 4		0.05
1.338 10 4
	1	0		1	2	3	4	5	6	7
	1					x				7
		Рис. 4.4.
7.	На	отрезке	mx	3 x	X mx	3 x	случайная		величина	X
	распределяется с вероятностью P(S3 ) 0,997 .
	Последнее свойство нормального распределения получило название
правила		трех сигм: на интервале mx 3 x					X mx	3 x рассеивается

примерно 99,7% значений случайной величины X .

Стаценко И.В. Лекция 4. Теория вероятностей и математическая статистика

1 / 21 2 > Следующая >>>

Соседние файлы в папке Лекции

#
16.05.20241.11 Mб0Л2-матстат.pdf
#
16.05.2024451.07 Кб0Л2-ТВ.pdf
#
16.05.2024829.51 Кб0Л3-матстат.pdf
#
16.05.2024394.41 Кб0Л3-ТВ.pdf
#
16.05.20241.09 Mб0Л4 - матстат.pdf
#
16.05.2024453.96 Кб0Л4-ТВ.pdf
#
16.05.20241.06 Mб0Л5-матстат.pdf
#
16.05.2024400.2 Кб0Л5-ТВ.pdf
#
16.05.2024377.37 Кб0Л6-матстат.pdf
#
16.05.2024489.81 Кб0Л6-ТВ.pdf
#
16.05.2024383.6 Кб0Л7-ТВ.pdf