Добавил:

Chupapi_Munyanya Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МЭИ»

Предмет:

Высшая математика

Файл:

Лекция 15

.pdf

Скачиваний:

Добавлен:

16.05.2024

Размер:

440.3 Кб

Скачать

☆

Лекция 15. Физический смысл дивергенции векторного поля. Физический смысл ротора векторного поля. Операторы Гамильтона и Лапласа. Обозначения курса ВМ-1

Лекция 15

1. Физический смысл дивергенции векторного поля

Рассмотрим объемную область пространства Oxyz , в каждой точке

M (x, y, z) которой, задано векторное поле

a M P M

Q M

R(M )k .

(1)

Ранее для данного пространства была введена скалярная величина

diva M

P M

Q M

R M

(2)

которая была названа дивергенцией.

Получим далее инвариантное (не зависящее от системы координат)
определение	дивергенции векторного				поля			a M .	Для чего	рассмотрим
вычисление	потока векторного			поля		a M через			некоторую	замкнутую
кусочно-гладкую поверхность				, расположенную					в объемной области
некоторого пространства.
По теореме Остроградского-Гаусса
	a, n 0 d div a dv .									(3)

Применим к тройному интегралу теорему о среднем значении
		a, n 0	d div			a	M *	V .		(4)

где V - объем области , сосредоточенный внутри замкнутой поверхности ;

точка M * . Откуда получим

Стаценко И.В. Лекция 15. Дивергенция. Ротор. Операторы Гамильтона и Лапласа

div

M *

a, n 0 d .

(5)

Далее, перейдя к пределу при M , получим

lim div

M *

div

lim

a, n 0 d .

(6)

M V

Определение 1.

Дивергенция

векторного

поля

a M в

точке M объемной

области

некоторого

пространства

является

пределом

отношения

потока

векторного поля через замкнутую поверхность, ограничивающую область

, к

объему области при стягивании области в точку.

Таким образом,

дивергенция векторного поля a M есть объемная плотность

потока векторного поля в точке M (физический смысл дивергенции).

Точки

области

которых div a M 0,

называют источниками

векторного поля.

Точки области , в которых div a M 0 , называют стоками векторного поля.

2. Физический смысл ротора векторного поля

Рассмотрим	инвариантное (не зависящее от системы		координат)
определение ротора	rot a M	векторного поля a M с непрерывными
координатами, используя полученную раннее формулу Стокса
	a, dr rot a , n 0 d .		(7)
	L

Пусть - часть плоскости с единичным вектором нормали n 0 , “натянутая” на контур L . При этом обход контура для наблюдателя из конца вектора нормали происходит против часовой стрелки.

Используя теорему о среднем для интеграла в правой части формулы (7), получим

a, dr	rot a , n 0 d S rot a M * , n 0 ,	(8)
L
где точка M * , S	- площадь поверхности .

Стаценко И.В. Лекция 15. Дивергенция. Ротор. Операторы Гамильтона и Лапласа

Тогда из (8) имеем

rot a M * , n 0		a, dr
		L		.
		S		.
		S
Откуда
Прn 0 rot a M *	a, dr
	L		.
		S	.
		S

Пусть далее d - диаметр контура L . Тогда при d 0 получим

M *

a, dr

lim

Пр

rot

lim

d 0

n 0

Тогда из (11) имеем

Прn 0 rot a M lim

a, dr

d 0

(9)

(10)

(11)

(12)

Таким образом, проекция ротора векторного поля на направление нормали к плоской поверхности, стягивающей контур L , не зависит от системы координат и равна поверхностной плотности циркуляции векторного поля по контуру L , т.е. равна поверхностной плотности работы векторного поля по перемещению материальной частицы по контуру L (в этом состоит физический смысл ротора векторного поля).

Известно также другое физическое истолкование ротора векторного поля применительно к задачам кинематики (раздела физики, изучающего движение тел).

Рассмотрим движение абсолютно твердого тела. Поле линейной скорости
v M точек M данного тела для	любого момента времени			определяется
формулой Эйлера
v v0			, r ,	(13)
		w

где

Стаценко И.В. Лекция 15. Дивергенция. Ротор. Операторы Гамильтона и Лапласа

v M ivx jvy kvz - вектор линейной скорости точки M ;

v0 M0 iv0 x jv0 y kv0 z - вектор линейной скорости точки M 0 ;

i x j y k z - вектор угловой скорости тела, проходящий через точку

M 0 ;

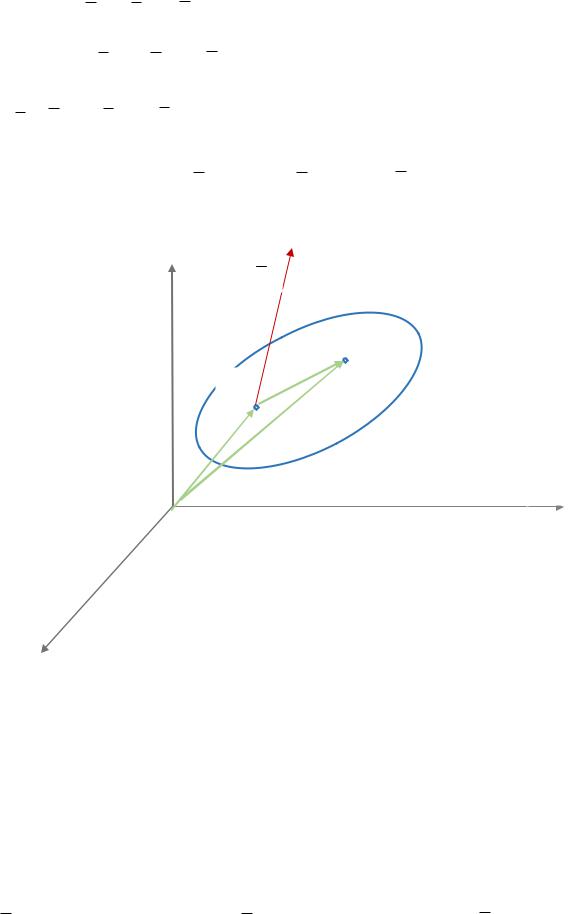
r r r0 x x0 i y y0 j z z0 k . см.рис.1.

M 0

Рис.1.

Тогда

, r

x - x0

y - y0

z - z0

i y z - z0 z y - y0 j x z - z0 z x - x0 k x y - y0 y x - x0 ;

Стаценко И.В. Лекция 15. Дивергенция. Ротор. Операторы Гамильтона и Лапласа

v0 x v M v0 w, r v0 yv0 z

	y z - z0 z y - y0
		x z - z0 z x - x0
		x z - z0 z x - x0
		x y - y0 y x - x0
		x y - y0 y x - x0

i vox y z - z0 z y - y0

j voy x z - z0 z x - x0

k voz x y - y0 y x - x0 vx i vy j vz k .

Ротор поля линейной скорости твердого тела определяется далее

следующим образом:

v M

rot

j 2

k 2

Таким образом, ротор поля линейных скоростей твердого тела в любой точке данного тела равен удвоенной угловой скорости.

3. Оператор Гамильтона и оператор Лапласа

Определение

2. Символ

называется

оператором

Гамильтона “набла”.

Если

ввести обозначения:

u u x, y, z

скалярное поле,

a M P M

Q M

R(M )k - векторное поле,

заданные в объемной

области пространства Oxyz .

использованием оператора

Гамильтона

формализуют все известные операторы векторного анализа следующим образом:

Стаценко И.В. Лекция 15. Дивергенция. Ротор. Операторы Гамильтона и Лапласа

k grad u ;

k u

u, l ux cos uy cos uz cos ul ;

где l cos

cos

cos k ;

, a

div a ;

, a

rot a .

(14)

(15)

(16)

(17)

Определение 3. Оператор вида div grad u , u называется оператором Лапласа скалярной функции u u x, y, z и обозначается в виде

u div grad u , u	2u		2u		2u
u div grad u , u	x2		y2		z2 .	(18)

4. Обозначения курса ВМ-1 (2 семестр)

b
1. f x dx - определенный интеграл от функции	f x	на отрезке a,b .
a

2. f x dx F (x) ba

F b F a - формула Ньютона-Лейбница.

Стаценко И.В. Лекция 15. Дивергенция. Ротор. Операторы Гамильтона и Лапласа

f x dx ,

x dx

несобственные интегралы на

бесконечном отрезке интегрирования.

dx lim

lim

несобственный интеграл с

бесконечным разрывом у функции f x внутри отрезка интегрирования.

x, y dxdy

двойной

интеграл

от

функции

x, y

по

DOxy

квадрируемой области DOxy .

x, y dxdy

x, y

- переход от двойного интеграла к

DOxy

повторному по области DOxy , правильной в направлении Oy .

w y

x, y dxdy

x, y

- переход от двойного интеграла к

DOxy

v y

повторному по области DOxy , правильной в направлении Ox .

x, y dxdy

cos

, sin

d d

переход

от

DOxy

двойного интеграла в декартовых координатах к двойному в полярных

координатах.

x, y, z dxdydz

тройной

интеграл от

функции

x, y, z

по

кубируемой области .

z2 x, y

10. f x, y, z dxdydz dxdy

f x, y, z dz - переход от тройного

Doxy

z1 x, y

интеграла к повторному по области , правильной в направлении Oz .

Стаценко И.В. Лекция 15. Дивергенция. Ротор. Операторы Гамильтона и Лапласа

DOxy ,

						8

11.		f	x, y, z dxdydz		f	cos( ), sin( ), z	d d dz - переход
				G
	от тройного интеграла в декартовых координатах к тройному в
	цилиндрических координатах.

f x, y, z dxdydz

f r cos sin , r sin sin , r cos r 2 sin drd d

-переход от тройного интеграла в декартовых координатах к тройному в сферических координатах.


13.		f	x, y, z d - поверхностный интеграл по дифференциалу площади

	поверхности от функции f x, y, z			по поверхности .


14.		f	x, y, z d - поверхностный интеграл по дифференциалу площади

	поверхности от функции f x, y, z			по замкнутой поверхности .

15.

x, y, z d

x, y, z

x, y

1 z

z dxdy - переход от

DOxy

поверхностного интеграла по дифференциалу площади поверхности по

поверхности к двойному по области DOxy .

a, n 0

z z

x, y

a, n 0

16.

dxdy - переход от поверхностного

DOxy

cos

интеграла по дифференциалу площади поверхности при вычислении потока векторного поля a по поверхности к двойному по области

где n o cos( )

cos

grad z z x, y

- вектор

grad z z x, y

внешней единичной нормали к поверхности : z z(x, y) .

Стаценко И.В. Лекция 15. Дивергенция. Ротор. Операторы Гамильтона и Лапласа

a, n 0

17. П

div

a dxdydz - переход от поверхностного

интеграла по дифференциалу площади поверхности при вычислении

потока векторного поля

a по замкнутой поверхности к тройному по

области (теорема Остроградского-Гаусса),

n o cos( )

cos

grad z z x, y

где

- вектор

grad z z x, y

внешней единичной нормали к поверхности : z z(x, y) .

18.

x, y, z dl

- криволинейный интеграл по дифференциалу длины дуги

от функции

f x, y, z по кривой L .

	t
	t
19. f (x, y, z)dl 1		f x t , y t , z t	x t 2	y (t) 2	z t 2 dt -
L	t0


переход от криволинейного интеграла по дифференциалу длины дуги от
функции	f x, y, z		по	кривой	L к определенному на отрезке
t t0 ,t1 для		кривой		L :	x x(t); y y(t); z z(t),заданной

параметрически.

20. P(x, y, z)dx Q(x, y, z)dy R(x, y, z)dz a, dr - криволинейный

L					L
интеграл по дифференциалам координат (линейный интеграл) от
			a M P(x, y, z)
векторного		поля	a M P(x, y, z)	i	Q(x, y, z)	j	R(x, y, z)k	-
линейный интеграл по кривой L .
21. a, dr
L
t1
P x t , y	t , z t x t Q x t , y t , z t y t R x t , y t , z t z t dt
t0
- переход от криволинейного интеграла по дифференциалам координат по
кривой	L	к определенному на отрезке t t0 ,t1 для кривой
L : x x(t);		y y(t);	z z(t),заданной параметрически.

Стаценко И.В. Лекция 15. Дивергенция. Ротор. Операторы Гамильтона и Лапласа

22. Ц a, dr - циркуляция векторного поля – линейный интеграл от

L
	a M P(x, y, z)
векторного поля	a M P(x, y, z)		i	Q(x, y, z)		j	R(x, y, z)k	-
линейный интеграл по замкнутой кривой L (обход кривой против часовой
стрелки).
		Q			P
23. Ц P(x, y)dx Q(x, y)dy					dxdy - формула Грина –
L	Doxy	x			y

переход

от

линейного

интеграла

плоском

поле

a M P(x, y, z)

Q(x, y, z)

по замкнутой кривой L

к двойному

интегралу по области DOxy (обход кривой против часовой стрелки).

24. Ц a, dr rot a , n o d

- формула

Стокса -

переход от

линейного

интеграла

поле

a M P(x, y, z)

по замкнутой кривой L

Q(x, y, z)

R(x, y, z)k

к поверхностному интегралу по поверхности (обход кривой против

часовой стрелки),

rot a M

где

n o cos( )i

cos j cos k -

вектор внешней единичной нормали к поверхности.

25.	a , dr M M 0 - вычисление линейного интеграла в
M 0M

потенциальном поле, где a grad		x, y, z	.

Рекомендуемая литература: Курс высшей математики. Кратные интегралы. Векторный анализ. Лекции и практикум: Учебное пособие/Под общ. Ред. И.М. Петрушко. 2-е изд. испр.– СПб: Издательство “Лань”, 2007. – 320 с.

Стаценко И.В. Лекция 15. Дивергенция. Ротор. Операторы Гамильтона и Лапласа

Соседние файлы в папке Лекции

#
16.05.2024458.2 Кб1Лекция 10.pdf
#
16.05.2024430.88 Кб2Лекция 11.pdf
#
16.05.2024449.15 Кб1Лекция 12.pdf
#
16.05.2024456.02 Кб0Лекция 13.pdf
#
16.05.2024416.26 Кб0Лекция 14.pdf
#
16.05.2024440.3 Кб0Лекция 15.pdf
#
16.05.2024440.55 Кб0Лекция 2.pdf
#
16.05.2024439.71 Кб0Лекция 3.pdf
#
16.05.2024456.92 Кб0Лекция 4.pdf
#
16.05.2024435.65 Кб0Лекция 5.pdf
#
16.05.2024384.5 Кб0Лекция 6-7.pdf