
ВМ 2 семестр / Лекции / Лекция 7
.pdf1
Лекция 7. Определение тройного интеграла. Свойства тройного интеграла. Вычисление тройного интеграла в декартовых координатах. Замена переменной в тройном интеграле. Тройной интеграл в цилиндрических координатах. Тройной интеграл в сферических координатах.
Лекция 7
Тройной интеграл
1.Определение тройного интеграла
Внекотором пространстве трех переменных рассмотрим кубируемую (имеющую объем) область . Пусть в данной области определена функция
трех переменных |
f (M ) , где M . |
|
|
|
|
|
||
|
Разобьем область произвольным образом на n |
кубируемых частей: 1 , |
||||||
2 , |
3 , …, n , не имеющих общих внутренних точек. В каждой области i |
|||||||
выберем произвольную точку Mi . |
|
|
|
|
|
|
||
|
Составим далее интегральную сумму |
|
|
|||||
|
|
n |
|
|
|
i |
i |
|
|
|
|
|
|
|
|||
|
|
|
f |
|
M |
V , |
(1) |
|
|
|
i 1 |
|
|
|
|
|
|
где |
Vi - объем области i . |
|
|
|
|
|
|
|
|
Пусть i |
- диаметр области i , а max i |
- максимальный диаметр |
|||||
|
|
|
|
|
|
|
i |
|
разбиения. |
|
|
|
|
|
|
|
|
Определение 1. |
Число I называется тройным интегралом по области от |
|||||||
функции f (M ) , если независимо от способа разбиения области |
на части i |
||||||||
и независимо от способа выбора точек |
Mi |
внутри области существует предел |
|||||||
интегральной суммы (1) при 0 в виде |
|
|
|||||||
|
|
n |
|
|
|
|
|
|
|
lim |
|
f |
|
M |
V I . |
(2) |
|||
0 |
|
|
|
i |
i |
|
|||
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Данный предел также обозначают следующим образом |
|
||||||||
|
|
I f M dV . |
(3) |
||||||
|
|
|
|
|
|
|
|
|
|
Теорема 1. Если функция f (M ) |
непрерывна в замкнутой кубируемой области |
||||||||
, то она интегрируема в данной области, т.е. существует тройной интеграл в виде (2).
Стаценко И.В. Лекция 7. Тройной интеграл
2
|
|
|
2. Свойства тройного интеграла |
|
|||||
|
|
Пусть f1 (M ) |
и f2 (M ) - функции, определенные и интегрируемые в |
||||||
некоторой кубируемой области . |
|
||||||||
1. |
|
1dV V , |
где V - объем области . |
|
|||||
|
|
|
|
|
|
|
|
|
|
2. |
|
С1 f1 M С2 f2 |
M dV C1 f1 M dV C2 f2 M dV , |
||||||
|
|
|
|
|
|
|
|
|
|
|
где C 1 , C 2 const . |
|
|
|
|
||||
3. |
|
f M dV f M dV f M dV , |
|
||||||
|
|
|
1 |
|
|
2 |
|
||
|
|
где 1 , 2 - две не пересекающиеся во внутренних точках области, |
|||||||
|
формирующие полный объем области . |
|
|||||||
4. |
f1 M dV f2 M dV , |
|
|||||||
|
|
|
|
|
|
|
|
||
|
если M |
f1 M f2 M . |
|
||||||
|
|
f M dV |
|
|
|
f M |
|
dV . |
|
|
|
|
|
|
|
||||
5. |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
6. |
V f M dV V , |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
если M |
f (M ) . |
|
||||||
7.Теорема о среднем. Если функция f (M ) непрерывна в замкнутой ограниченной области , то в данной области существует точка , такая, что
Стаценко И.В. Лекция 7. Тройной интеграл
|
|
|
|
|
3 |
|
|
|
|
|
|||||
|
f |
|
M |
|
dV f |
|
V . |
|
|
|
|
|
|
|
|
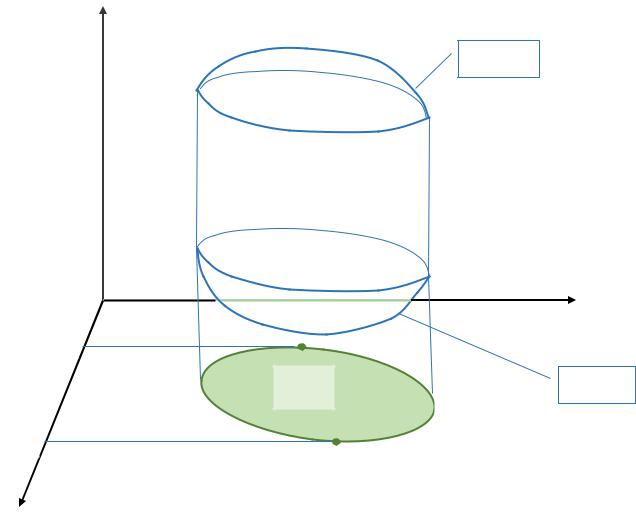
3. Вычисление тройного интеграла в декартовых координатах
В пространстве Oxyz рассмотрим кубируемую (имеющую объем)
замкнутую область . Пусть в данной области определена функция трех |
||
переменных f (M ) , где M x, y, z . |
|
|
Тройной интеграл от функции |
f (M ) по области имеет вид |
|
f M dV |
f x, y, z dxdydz . |
(4) |
|
|
|
Рассмотрим способ сведения тройного интеграла к повторному, полагая, что область интегрирования является правильной в направлении Oz (см.
рис.1).
z
z2 x, y
|
A |
|
|
y |
a |
|
|
|
|
|
|
|
|
|
y1 x |
Doxy |
y2 |
x |
z1 x, y |
|
|
|
b |
B |
x
Рис.1.
Стаценко И.В. Лекция 7. Тройной интеграл
4
Область Doxy является проекцией объемного тела на плоскость z 0 в
направлении оси Oz . В свою очередь, область Doxy проецируется на ось Ox в
виде отрезка a,b .
Далее будем полагать, что выполняются следующие ограничения.
Область Doxy является замкнутой и правильной в направлении Oy , т.е.
выполняются два условия: |
|
1. Граница области Doxy состоит из двух гладких функций y1 |
x и |
y2 x , разделенных точками A и B см. рис.1. |
|
2.Любой луч, проведенный из отрезка a,b в направлении Oy пересекает границы области Doxy ровно два раза.
Область интегрирования является замкнутой и правильной в направлении Oz , т.е. выполняются два условия:
1.Нижняя и верхняя границы тела - поверхности, соответственно, z1 x, y и z2 x, y являются гладкими поверхностями.
2.Любой луч, проведенный из области Doxy через объемное тело в направлении Oz , пересекает его нижнюю и верхнюю границы каждую ровно по одному разу.
Теорема 2. Пусть существует тройной интеграл вида
f M dV f x, y, z dxdydz , |
(4) |
|
|
|
|
и для любой точки M Doxy существует определенный интеграл
z2 |
x, y |
|
F (x, y) |
f (x, y, z)dz , |
(5) |
z1 x, y |
|
|
тогда тройной интеграл (4) можно вычислять в виде следующего повторного интеграла
Стаценко И.В. Лекция 7. Тройной интеграл
5
|
|
|
z2 |
x, y |
|
|
f x, y, z dxdydz dxdy |
|
f x, y, z dz . |
(6) |
|||
|
|
Doxy |
z1 x, y |
|
|
|
Интеграл (6), в свою очередь, можно представить в виде |
|
|||||
|
z2 x, y |
b |
y2 x |
z2 |
x, y |
|
dxdy |
|
f x, y, z dz dx |
|
dy |
f (x, y, z)dz . |
(7) |
Doxy |
z1 x, y |
a |
y1 x |
z1 x, y |
|
|
Пример 1. Вычислить интеграл x y z dxdydz по объемному телу ,
|
|
|
|
|
|
ограниченному плоскостями x 0; |
x 1; |
y 0; |
y 1; |
z 0; |
z 1. |
Решение. Объемное тело представляет собой куб – область интегрирования, правильная по направлениям Ox , Oy , Oz . Тогда
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
x y z dxdydz dx dy (x y z)dz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
1 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
dx dy (x y z)d |
z x y dx dy |
x y z |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
1 |
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
0 |
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
1 |
1 |
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
1 |
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
dx dy |
|
|
1 |
x y |
|
|
|
|
|
|
0 |
x y |
|
|
|
|
|
|
|
|
|
dx 1 x y |
|
|
|
|
|
d |
|
|
|
x y |
|
1 |
|
|||||||||||||||||||||||
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1 |
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
||||||
|
|
|
dx x y 2 d x y |
dx 1 x y 3 |
1 dx x y 3 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
2 x 3 dx |
|
|
1 x 3 dx |
|
1 x 3 dx |
|
x3dx |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
6 |
6 |
6 |
6 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 x |
|
4 |
1 |
|
1 x |
|
4 |
|
|
1 |
x4 |
|
1 |
|
3 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
24 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Стаценко И.В. Лекция 7. Тройной интеграл

6
4.Замена переменной в тройном интеграле
В пространстве Oxyz рассмотрим кубируемую (имеющую объем)
замкнутую область |
. Пусть в данной области определена функция трех |
|||
переменных f (M ) , где M x, y, z . |
|
|
||
Тройной интеграл от функции |
f (M ) по области имеет вид |
|
||
|
f M dV |
f x, y, z dxdydz . |
(8) |
|
|
|
|
|
|
Теорема 3. Пусть выполняются следующие условия. |
|
|||
1. Существует |
взаимно однозначное |
отображение точек |
u,v, w |
|
кубируемой области G на точки x, y, z |
кубируемой области в виде |
|||
|
x x u,v, w , |
(9) |
||
|
y y u,v, w , |
(10) |
||
|
z z u,v, w . |
(11) |
||
2.Функции x x u,v, w , y y u,v, w , z z u,v, w непрерывны вместе со своими частными производными первого порядка.
3.Якобиан отображения
|
|
x |
x |
x |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
u |
v |
w |
|
|
|
|
J u,v, w |
|
y |
y |
y |
|
0 . |
(12) |
|
u |
v |
w |
||||||
|
|
|
|
|
||||
|
|
z |
z |
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
v |
w |
|
|
|
Тогда справедлива формула замены переменной в тройном интеграле
f x, y, z dxdydz f x u,v, w , y u,v, w , z u,v, w J dudvdw .
G
(13)
Стаценко И.В. Лекция 7. Тройной интеграл
7
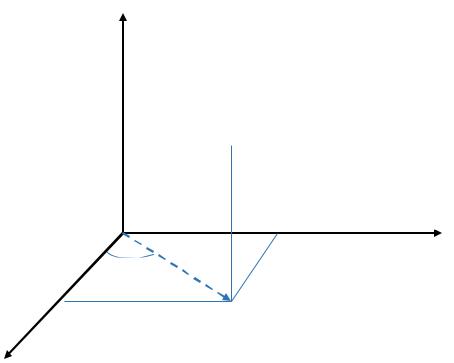
5.Тройной интеграл в цилиндрических координатах
Точка трехмерного пространства в цилиндрических координатах см. рис. 2. представляется тремя переменными , , z , связанными с декартовыми
координатами x, y, z следующими соотношениями:
|
|
|
|
|
|
|
|
x cos |
|
|
, |
0 , |
0 2 . |
(14) |
|
|
|
|
|
|
|
|
|
|
y sin |
|
, |
(15) |
|||
|
|
|
|
z z . |
|
|
(16) |
z |
z |
 M , , z
M , , z
y
y |
x
|
x
Рис.2.
Якобиан перехода от декартовых координат к цилиндрическим имеет вид
|
|
x |
|
x |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
- sin |
0 |
|
|
|
|
|
|
|
|
|
||||||
|
|
y |
|
y |
|
y |
|
|
|
|||
J , , z |
|
|
|
|
|
sin |
cos |
0 |
. |
|||
|
|
|
|
z |
||||||||
|
|
|
|
|
|
0 |
0 |
1 |
|
|||
|
|
z |
|
z |
|
z |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Стаценко И.В. Лекция 7. Тройной интеграл

8
Тогда формула перехода в тройном интеграле от декартовых координат к цилиндрическим имеет вид
f x, y, z dxdydz f x , , z , y , , z , z , , z d d dz .
|
G |
|
(17) |
Пример 2. Вычислить интеграл x2 y2 dxdydz по объемному телу ,
ограниченному плоскостью z 0 и параболоидом z 1 x2 y2 .
Решение. Запишем систему неравенств для области интегрирования G в цилиндрических координатах.
|
При |
z 0 |
|
|
на |
плоскости |
имеем |
круговую |
область |
интегрирования |
|||||||||||||||||||||||
oxy |
|
|
|
|
|
|
|
x2 y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
D |
|
|
x, y |
|
: 0 |
|
1 . Объемное тело |
моделируется следующей |
|||||||||||||||||||||||||
системой неравенств: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
: 0 x2 y2 |
|
|
|
1 x2 y2 . |
|
|
||||||||||||
|
|
|
|
|
|
|
|
x, y, z |
|
|
1; |
0 z |
|
|
|||||||||||||||||||
|
|
Тогда объемное тело G в цилиндрических координатах моделируется |
|||||||||||||||||||||||||||||||
следующей системой неравенств: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
G |
|
|
, , z |
: 0 |
|
2 |
1, 0 2 , 0 z 1- 2 . |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С учетом того, что |
|
|
0 |
2 1 |
|
0 |
1 |
|
получим следующий |
||||||||||||||||||||||
повторный интеграл в цилиндрических координатах |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
1 |
|
1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
y2 dxdydz |
d 2d |
|
dz . |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
1 |
|
|
|
|
1 2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
4 |
|
1 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
||||||||||||||
|
|
d 2d |
dz 2 3 1 2 d 2 |
|
|
|
|
|
|
|
|
|
. |
||||||||||||||||||||
|
|
4 |
6 |
|
6 |
||||||||||||||||||||||||||||
|
|
0 |
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Стаценко И.В. Лекция 7. Тройной интеграл
9
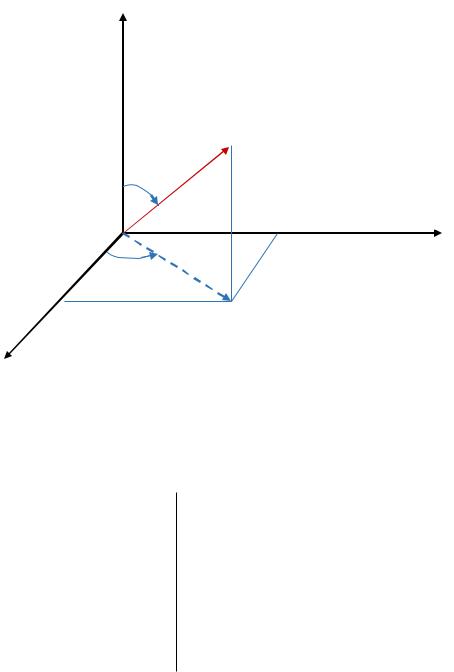
6.Тройной интеграл в сферических координатах
Точка трехмерного пространства в сферических координатах см. рис. 3. представляется тремя переменными r, , , связанными с декартовыми
координатами x, y, z следующими соотношениями:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x r cos |
|
|
sin |
|
, |
r 0 , |
|
0 2 , |
0 |
(18) |
|||||
|
|
|
|
y r sin |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
sin |
|
, |
|
(19) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z r cos |
|
. |
|
|
|
(20) |
|||
z |
z
 M r, ,
M r, ,
r
y
y |
x
x
Рис.3.
Якобиан перехода от декартовых координат к сферическим имеет вид
|
|
x |
x |
|
x |
||
|
|
|
|||||
|
|
r |
|
|
|
||
|
|
|
|
|
|||
J r, , |
|
y |
y |
|
y |
||
r |
|
|
|
||||
|
|
|
|||||
|
|
z |
z |
|
z |
||
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
cos |
|
|
|
|
|
sin |
|
-r sin |
|
|
|
|
|
sin |
|
rcos |
|
cos |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
sin |
|
|
|
|
|
sin |
|
rcos |
|
|
|
|
sin |
|
|
|
r sin |
|
|
cos |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
cos |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
-rsin( ) |
|
|
|
|||||
Стаценко И.В. Лекция 7. Тройной интеграл
10
Вычисление определителя дает следующий результат:
J r, , r2 cos2 sin |
|
-sin( ) |
cos( ) |
|
r sin3 |
( ) |
|
cos( ) |
-rsin( ) |
|
|
|
|
|
|
||||||||
|
cos( ) |
sin( ) |
|
|
sin( ) |
rcos( ) |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
r2 cos2 sin r2 sin3 ( ) r2 sin .
Таким образом, для отображения переменных (18-20)
|
|
|
|
r2 sin |
|
|
|
|
J |
|
r, , |
|
|
|
. |
(21) |
Тогда формула перехода в тройном интеграле от декартовых координат к cферическим при отображении (18-20) имеет вид
f x, y, z dxdydz f x r, , , y r, , , z r, , r 2 sin drd d
|
G |
|
|
|
|
|
|
|
(22) |
||
Пример 3. |
Вычислить интеграл |
x2 y2 z2 dxdydz по объемному телу |
|||
|
|
|
|
|
|
|
|
|
|
|
|
, ограниченному плоскостью |
z 0 и половиной сферы z |
1 x2 y2 . |
|||
Решение. Запишем систему неравенств для области интегрирования G в сферических координатах.
|
При |
z 0 |
на |
плоскости имеем круговую |
область интегрирования |
||||||
oxy |
|
|
|
|
|
|
x2 |
y2 |
|
|
|
D |
|
|
x, y |
|
: 0 |
1 . Объемное тело |
|
моделируется следующей |
|||
системой неравенств:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x, y, z |
|
: 0 |
x2 |
y2 |
1; |
0 z 1 x2 y2 . |
||
Тогда объемное тело G в сферических координатах моделируется следующей системой неравенств:
|
r 1, 0 |
2 , 0 |
|
|
G r, , : 0 |
. |
|||
|
|
|
|
2 |
Стаценко И.В. Лекция 7. Тройной интеграл
