Добавил:

Chupapi_Munyanya Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МЭИ»

Предмет:

Высшая математика

Файл:

Лекция 5

.pdf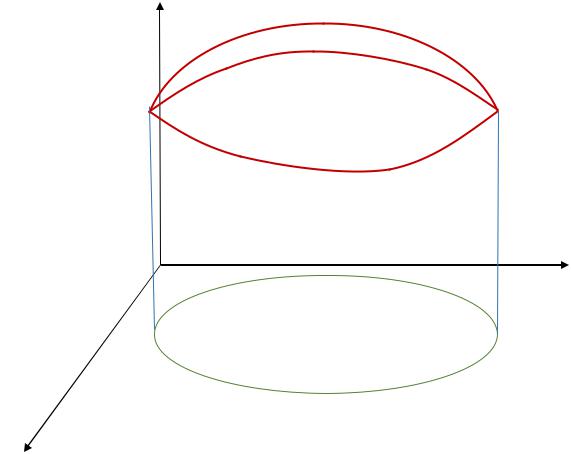

Скачиваний:

Добавлен:

16.05.2024

Размер:

435.65 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

Лекция 5. Двойной интеграл. Объем цилиндрического тела. Двойной интеграл определение. Свойства двойного интеграла. Вычисление двойного интеграла в декартовых координатах.

Лекция 5

Двойной интеграл

1.Объем цилиндрического тела

Всистеме координат Oxyz на плоскости Oxy зададим некоторую

ограниченную квадрируемую (имеющую площадь) область D . Пусть в области

D определена	непрерывная	функция	двух переменных	z f (x, y) 0 .
Рассмотрим цилиндрическое тело , ограниченное снизу областью D , сверху
поверхностью	z f (x, y) 0 ,	по бокам	– цилиндрической	поверхностью с

образующими, параллельными оси Oz см. рис. 1. Поставим задачу найти объем V данного тела .

f (x, y)

Рис.1.

Стаценко И.В. Лекция 5. Двойной интеграл.

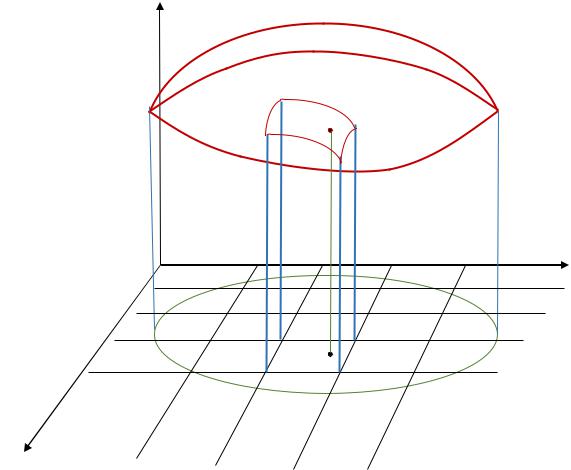
Разобьем область D на n квадрируемых (имеющих площадь) областей Dk , не имеющих попарно общих точек (k 1, 2,3,..., n) см. рис.2. Обозначим

площадь

области

Dk как

Sk . Тогда

площадь

области

D определяется

как

S Sk .

Внутри каждой области Dk

выберем точку M k

с координатами

k 1

xk , yk .

Найдем значения функции

f Mk в каждой точке

M k . Поднимем

высоты

из

угловых точек

области

до

пересечения с

поверхностью

z f (x, y) 0 .

Соединяя

данные

высоты

кратчайшими

линиями

на

поверхности,

получим

поверхности,

ограничивающие

каждую область

Dk сверху.

В результате над каждой областью Dk формируется объемное тело

k . Пусть

объем

данного тела имеет обозначение Vk .

Тогда

объем

тела

можно найти как V Vk .

k 1

f (M k )

M k

Рис.2.

Стаценко И.В. Лекция 5. Двойной интеграл.

Пусть	k - расстояние между двумя наиболее удаленными точками области
Dk , а	max k - диаметр разбиения области D . При			0 объем Vk
	k
каждого тела k можно приближенно считать по формуле
	Vk f Mk Sk ,		(k 1, 2,3,..., n) .	(1)
Тогда объем тела можно найти по формуле
		n
	V lim f		M k Sk .	(2)
	0	k 1
		k 1

2.Двойной интеграл определение

Внекоторой системе координат на плоскости зададим ограниченную

квадрируемую область	D . Пусть в каждой точке M области D определена
ограниченная функция двух переменных f f (M ) .
Разобьем область	D на n квадрируемых (имеющих площадь) областей

Dk , не имеющих попарно общих точек (k 1, 2,3,..., n) . Обозначим площадь

		n
области Dk как Sk . Тогда площадь области D определяется как S Sk .
		k 1
Внутри каждой области Dk	выберем точку M k . Найдем значения функции
f Mk в каждой точке M k .	Пусть k - расстояние между двумя наиболее
удаленными точками области	Dk , а max k	- диаметр разбиения области
	k
D .
Составим интегральную сумму для функции		f f (M ) по области D
	n
	f M k Sk .	(3)

k 1

Определение 1. Если независимо от способа разбиения области D на части Dk , существует конечный предел интегральной суммы (3) в виде

	n
I lim f M k Sk ,		(4)
0	k 1
	k 1

Стаценко И.В. Лекция 5. Двойной интеграл.

4
то данный предел называется двойным интегралом от функции	f f (M ) по
области D и обозначается следующим образом:
I f (M )ds .	(5)
D

Замечание 1. Двойной интеграл в виде (5) введен для произвольной системы координат. В системе координат Oxyz двойной интеграл от функции z z(x, y) по области D на плоскости Oxy может иметь следующее обозначение:

I z(x, y)dxdy .	(6)
D

Замечание 2. В формуле (6) произведение дифференциалов двух независимых переменных dxdy формирует дифференциал площади ds на плоскости Oxy . В данном случае dxdy ds .

Геометрический смысл двойного интеграла I z(x, y)dxdy : Пусть в каждой

		D
точке	M области	D на плоскости Oxy определена непрерывная

неотрицательная функция двух переменных z z(x, y) 0 . Тогда двойной интеграл I z(x, y)dxdy есть объем некоторого цилиндрического тела ,

формируемого между поверхностью функции z z(x, y) 0 и площадью области D на плоскости Oxy , с направляющими параллельными оси Oz .

Определение 2. Область D называется замкнутой, если граничные точки области (граница области) принадлежит данной области.

Далее будем полагать, что функция f (M ) интегрируема в области				D , т.е.
существует двойной	интеграл	вида I z(x, y)dxdy ,	если	функция
		D
f (M ) непрерывна в	замкнутой	квадрируемой области D	или	функция

ограничена в области D и непрерывна во всей квадрируемой области D , кроме граничных точек.

Стаценко И.В. Лекция 5. Двойной интеграл.

3.Свойства двойного интеграла

1.(Интеграл от дифференциала площади)

1ds S , где S - площадь области D .

2. (Линейность) Пусть функции	f1 (M ) и	f2 (M ) интегрируемы в области
D . Тогда
f1 M f2 M ds f1 M ds f2 M ds ,
D	D	D
где , const .

3.(Аддитивность) Пусть область D разделена на две области D1 и D2 , не имеющие общих внутренних точек. Тогда

f M ds f M ds f M ds .

D	D1	D2
4. (Интегрирование	неравенств)	Пусть	функции f1 (M ) и f2 (M )
интегрируемы в	области D ,	при этом	M D	f1 (M ) f2 M .

Тогда

f1 M ds f2 M ds .

D D

5.	(Оценка 1) Пусть функция f (M ) интегрируема в ограниченной области
	D ,	при этом M D	A f M B .	Тогда
		A S f M ds B S ,
			D
	где S - площадь области D .
6.	(Оценка 2 (по модулю))		Пусть функция	f (M ) интегрируема в области
	D .	Тогда

Стаценко И.В. Лекция 5. Двойной интеграл.

	6
f M ds f M ds ,
D	D

где S - площадь области D .

7. (Теорема о среднем) Пусть функция f (M ) непрерывна в замкнутой

ограниченной области D , тогда в данной области существует точка M * , такая, что

f M ds f M * S ,

где S - площадь области D .

4.Вычисление двойного интеграла в декартовых координатах

Вдекартовой системе координат Oxyz на плоскости Oxy рассмотрим

простую (правильную) в направлении Oy область D . Данная область характеризуется следующими ограничениями:

1.D x, y : a x b; 1 x y 2 x ,

где 1 x , 2 x - функции, заданные на отрезке a,b .

2.Любой луч, проведенный в области D в направлении Oy , пересекает

границы данной области ровно два раза.

y	y 2	x

y 1 x

Рис. 3.

Стаценко И.В. Лекция 5. Двойной интеграл.

Теорема 1. Если функция z z(x, y) интегрируема в области D , правильной в

направлении Oy ,

такой, что D

x, y

: a x b;

, где

1 x , 2 x

функции, непрерывные

на отрезке

a,b и

x a,b

существует интеграл

2 x

S x z x, y dy ,

1 x

то двойной интеграл z x, y dxdy существует и может быть вычислен в виде

повторного интеграла следующим образом:

	b 2 x
z x, y dxdy

D	a 1 x

Доказательство:

z x, y dy dx . (7)

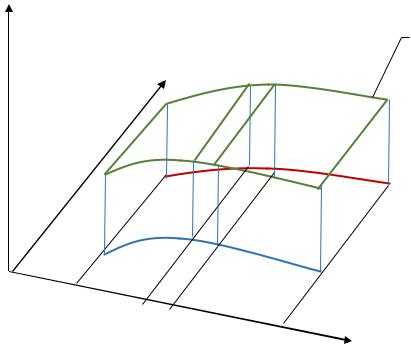
Рассмотрим случай, когда M x, y D функция z(x, y) 0 см. рис. 4.

		y			z x, y
			S x
				S x dx
				S x dx
				2 x
		D
0				1 x
a	x
	x		x dx	x
			x dx
			b
			b
Рис. 4.

Стаценко И.В. Лекция 5. Двойной интеграл.

Объем тела , представленного на рис. 4. можно вычислить двумя способами. Первый способ следует из геометрического смысла определенного интеграла

V z x, y dxdy .	(8)
D
Второй способ основан на вычислении	элементарного объема ,

сформированного в рамках тела между сечениями данного тела плоскостями

x C1 const

и x dx C2

const

см.

рис. 4. После суммирования таких

элементарных объемов на всем отрезке a,b можно также получить объем тела

Найдем далее объем тела по приближенной формуле

2 x

x, y dy

dx .

(9)

1 x

Формула (9) работает тем точнее, чем меньше величина dx . Тогда объем всего тела можно найти по формуле

b 2 x

x, y dy

dx .

(10)

a 1 x

Замечание 3. Интегрирование внутреннего интеграла в формулах (7) и (10)

проводится с учетом	того, что переменная x	для внутреннего интеграла
является константой.
В декартовой	системе координат Oxyz на	плоскости Oxy рассмотрим

простую (правильную) в направлении Ox область D см. рис. 5. Данная область характеризуется следующими ограничениями:

1.D x, y : c y d; 1 y x 2 y ,

где 1 y , 2 y - функции, заданные на отрезке c, d .

2.Любой луч, проведенный в области D в направлении Ox , пересекает

границы данной области ровно два раза.

Теорема 2. Если функция z z(x, y) интегрируема в области D , правильной в

направлении Ox ,

такой, что D

x, y

: c y d;

, где

1 y , 2 y

функции, непрерывные на отрезке

c, d и

y c, d

существует интеграл

Стаценко И.В. Лекция 5. Двойной интеграл.

2 x

S x z x, y dy ,

1 x

то двойной интеграл z x, y dxdy существует и может быть вычислен в виде

повторного интеграла следующим образом:

	d 2 y
z x, y dxdy

D	c 1 y

z x, y dx dy . (11)

Замечание	4.	Интегрирование	внутреннего	интеграла в формуле	(11)
проводится	с	учетом того, что	переменная	y для внутреннего интеграла

является константой. y

	D
1 y	2 y

Рис. 5.

Замечание 5. Если область интегрирования D не является правильной в какомлибо направлении, ее можно разбить на правильные области линиями параллельными осям Ox , Oy .

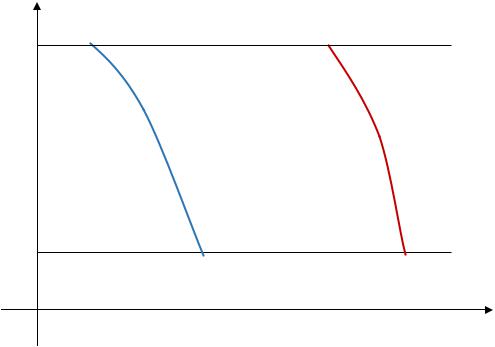
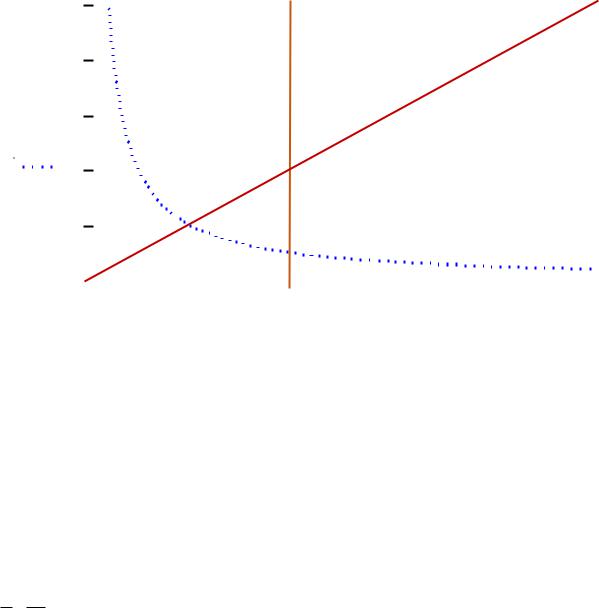
Пример 1. Найти интеграл xydxdy по области D , заданной следующим

образом:

		1
D x, y :1	x 2;		y x .
D x, y :1	x 2;	x	y x .
		x
См. рис.6.
Стаценко И.В. Лекция 5. Двойной интеграл.

		5
		5
		4.5
		4.5
		4
		4
		3.5
		3.5
f1( x)		3
		3


f2( x)	2.5
f2( x)	2.5
		2
		2
		1.5
		1.5	D
		1	D
		1
		0.5

	0		0.5	1	1.5	2		2.5		3			3.5		4		4.5	5
								x
	Рис. 6.
Решение:	Область интегрирования является правильной в направлении Oy и
не является правильной в направлении Ox .
1 способ. Вычислим интеграл по формуле (7)
							x													2
							x													2
	2 x				2	y2			1	2		3		1		1	x4
	2 x				2	y2			1			3		1		1	x4
xydxdy			xy dy dx x					dx			x				dx			ln	x
									2					x		2

D	1	1			1	2	1			1							4			1
D	1				1	2				1							4			1
	x						x

1 15 ln 2 .

2 4

2 способ. Вычислим интеграл по формуле (11), предварительно разбив линией

y 1 область интегрирования D на две более простые области D1																																и D2 см. рис
7.
Тогда
					1			2						2		2						dy		1	1	4 y		1	dy		1 2
	xydxdy				1			2		xy	dx dy			2		2		xy		dx				1				1			1 2	4 y y3		dy
	xydxdy									xy	dx dy							xy		dx												4 y y3		dy

																								2 0.5				y			2 1
D					0.5			1						1 y										2 0.5				y			2 1
							y
	1	2 y							1			1 2			y		4		2		1 3						1 9			1 15
																			2

			2
				ln		y			0,5				2 y										ln 2										ln 2 .


	2										2				4				1		2	2					2 4			2	4
	2										2				4						2	2					2 4			2	4

Стаценко И.В. Лекция 5. Двойной интеграл.

1 / 21 2 > Следующая >>>

Соседние файлы в папке Лекции

#
16.05.2024416.26 Кб2Лекция 14.pdf
#
16.05.2024440.3 Кб2Лекция 15.pdf
#
16.05.2024440.55 Кб4Лекция 2.pdf
#
16.05.2024439.71 Кб2Лекция 3.pdf
#
16.05.2024456.92 Кб2Лекция 4.pdf
#
16.05.2024435.65 Кб2Лекция 5.pdf
#
16.05.2024384.5 Кб2Лекция 6-7.pdf
#
16.05.2024459.54 Кб3Лекция 6.pdf
#
16.05.2024449.5 Кб2Лекция 7.pdf
#
16.05.2024447.02 Кб3Лекция 8.pdf
#
16.05.2024453.54 Кб3Лекция 9.pdf