Добавил:

Chupapi_Munyanya Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МЭИ»

Предмет:

Высшая математика

Файл:

Лекция 1

.pdf

Скачиваний:

Добавлен:

16.05.2024

Размер:

472.48 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

Курс ВМ-1

(2 семестр)

(16 лекций)

Темы:

1.Определенный интеграл.

2.Кратный интеграл.

3.Элементы теории поля

Стаценко И.В. Лекция 1. Определенный интеграл.

Лекция 1.

Площадь криволинейной

трапеции. Определенный интеграл.

Свойства

определенного интеграла. Производная интеграла по верхнему пределу. Формула

Ньютона-Лейбница.

Лекция 1

Определенный интеграл

Площадь криволинейной трапеции

Рассмотрим

функцию f (x) ,

заданную

на

отрезке

a,b .

Пусть

x a,b

f (x) 0 . Разобьем отрезок a,b на n отрезков точками

x0 a x1 x2 x3 ... xn 1 xn

b .

(1)

Введем обозначения полученных отрезков

xk xk xk 1 ,

k 1, 2,3,..., n.

(2)

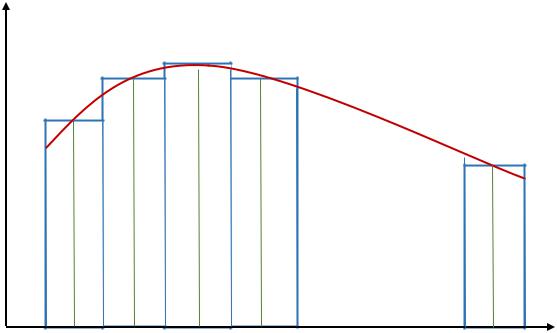
Внутри каждого отрезка выберем точку k ,

k 1, 2,3,..., n,

проведем

высоту f k

построим прямоугольники с основаниями

и высотами

f k см. рис 1.

f (x)

x1 2 x2

4 x4

.........

xn 1

рис.1.

Стаценко И.В. Лекция 1. Определенный интеграл.

Найдем площадь	Sф ступенчатой			фигуры,	составленной из
прямоугольников
		n
	Sф xk f			k .	(3)
		k 1
Пусть
max xk ,			k 1,2,3,..., n.		(4)
	k
Далее найдем величину
		n
	S lim	xk f		k .	(5)
	0	k 1
		k 1

Очевидно, что данный предел есть предельная величина площади ступенчатой фигуры при стремлении к нулю длин отрезков разбиения исходного отрезка

a,b . Данная предельная величина есть площадь криволинейной трапеции, ограниченной сверху графиком функции f (x) , и с основанием равным длине отрезка a,b .

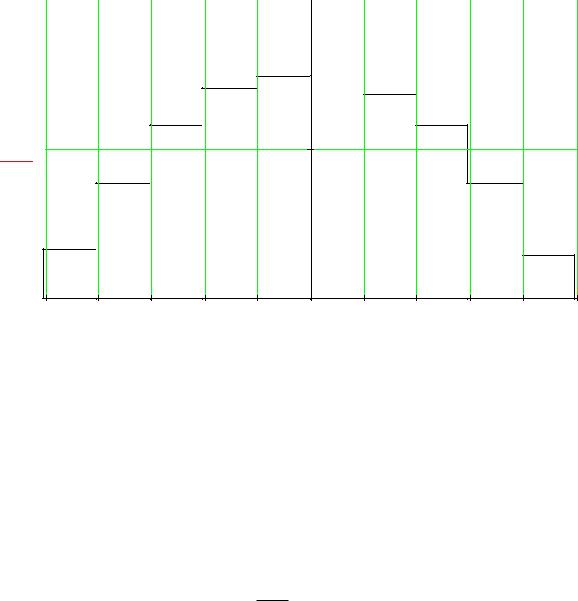
Пример 1.

Найти площадь криволинейной трапеции под графиком функции

f (x) 3 1 x2

на отрезке

a,b

1,1 , используя формулу (3) для n 10 c

постоянным шагом k xk

k 1,2,3,...,10

и выбором точек k в центре

каждого частичного отрезка.

Решение:

Определяем шаг интегрирования h

b a

Определяем координаты точек k

по формулам

;

h ; i 2,3, 4,...,10 .

i 1

Получим

0,9;

-0,7;

-0,5;

-0,3;

-0,1; 0,1; 0,3; 0,5; 0,7; 0,9

Вычисляем интегральную сумму по формуле

Sф h f k .

k 1

Sф 0,2 0,57 1,53 2,25 2,73 2,97 2,97 2,73 2,25 1,53 0,57 4,02.

Точный результат в данном случае S 4.

Стаценко И.В. Лекция 1. Определенный интеграл.

						4
						4
f ( x)						2
1	0.8	0.6	0.4	0.2		0	0.2	0.4	0.6	0.8	1
						x
					рис.2.
Пример 2. Найти площадь криволинейной трапеции под графиком функции
f (x) 3	1 x2	на отрезке		a,b		1,1 , используя формулу (3)					для n 100

c постоянным шагом			k xk h		k 1,2,3,...,100				и выбором точек k в
центре каждого частичного отрезка.

Решение:

2 100

Sф 100 k 1 f k 4,0002 .

2.Определенный интеграл

Рассмотрим функцию	f (x) ,	заданную на отрезке	a,b . Разобьем
отрезок a,b на n отрезков точками
x0 a x1 x2 x3 ... xn 1 xn b .			(6)
Введем обозначения полученных отрезков
xk xk	xk 1 ,	k 1, 2,3,..., n.	(7)

Стаценко И.В. Лекция 1. Определенный интеграл.

5
Внутри каждого отрезка выберем точку k , k 1, 2,3,..., n.
Пусть
max xk ,	k 1,2,3,..., n.	(8)
k
Составим сумму
n
S xk	f k .	(9)
k 1
Данная сумма называется интегральной суммой для функции		f (x) на

отрезке a,b .

Определение 1. Если существует конечный предел интегральных сумм (9) при0, не зависящий от способа разбиения отрезка a,b на части и от выбора

точек k , то этот предел называется определенным интегралом от функции
f (x) на отрезке a,b и обозначается в виде
b		n
	f (x)dx lim	n	x f	k	.	(10)
	0		k	k
a		k 1

Числа a и b называются нижним и верхним пределами интегрирования.

Если определенный интеграл в виде (10) существует, то функция f (x) называется интегрируемой по Риману на отрезке a,b .

(Понятие определенного интеграла в виде (10) принадлежит немецкому математику Бернхарду Риману, 1826-1866).

Теорема 1. Если выполняется хотя бы одно из следующих условий:

1.Функция f (x) непрерывна на отрезке a,b .

2.Функция f (x) ограничена на отрезке a,b и имеет на данном отрезке конечное число точек разрыва.

3.Функция f (x) монотонна на отрезке a,b .

То функция f (x) называется интегрируемой по Риману на отрезке a,b .

Стаценко И.В. Лекция 1. Определенный интеграл.

Свойства определенного интеграла

Пусть функция

f (x) интегрируема на отрезке

a,b .

Тогда справедливы

следующие свойства определенного интеграла.

f (x)dx 0.

f (x)dx f (x)dx .

Доказательство:

f (x)dx lim n

lim n

x f

f (x)dx ,

т.к.

i 1

k 1

xi xi 1 0 ,

x0 b ,

xn a .

dx b a .

Доказательство:

1dx lim

n x

b a .

k 1

(Линейность)

Пусть функции

f1 (x) и

f2 (x)

интегрируемы на отрезке

a,b , а

с1,с2 const . Тогда

с1 f1 x c2 f2 (x) dx c1 f1

x dx c2 f2 x dx .

Доказательство:

Так как функции

f1 (x) и

f2 (x)

интегрируемы на отрезке

a,b ,

то для каждой функции по отдельности

получим

c1 f1 (x)dx lim xk c1 f1 k c1 lim

xk f1 k c1 f1 (x)dx ;

k 1

Стаценко И.В. Лекция 1. Определенный интеграл.

f2 (x)dx lim xk c2

f2 k c2 lim xk f2

c2 f2 (x)dx .

k 1

0 k 1

Из существования пределов

с1 lim xk f1 k

с2 lim xk f2 k

по

k 1

свойствам пределов следует и существование предела

lim с

x f

n x f

с lim

k 1

В сокращенной записи получим:

lim n с f с f x

1 1 k 2 2 k k 0 k 1

Откуда следует, что

с1 f1 x c2 f2 (x) dx

lim

x f

с lim

x f

k 1

b	b
c1 f1	x dx c2 f2	x dx .
a	a

Следствие 1.	Пусть функции				f1 (x) , f2 (x) , … ,		fn (x) интегрируемы на
отрезке a,b , а	с1,с2 ,...,cn const . Тогда
	b		n		n	b
			ci	fi (x) dx ci fi x dx			.
	a	i 1			i 1	a

5.	(Аддитивность)
Пусть отрезок a,b разбивается на два отрезка: a,c и с,b ,				a c b.
Тогда
	b	с	b
	f x	dx f x dx f x dx .
	a	a	с
Следствие 2.	Для любых чисел:		c1 ,c2 ,c3 справедлива формула

Стаценко И.В. Лекция 1. Определенный интеграл.

	с2	с3		с2
	f x dx f x dx f				x dx .
	с1	с1		с3
Доказательство:	Для случая		c1 c3	c2	см. свойство 5.

Для других случаев, допустим, что c1 c2 c3 , тогда по свойству 5

	с3	с2	с3
	f x dx f		x dx f	x dx .
	с1	с1	с2
Откуда получим
с2	с3	с3	с3	с2
f	x dx f	x dx f x dx		f x dx	f x dx .
с1	с1	с2	с1	с3
Допустим, что	c3 c1 c2 , тогда по свойству 5
	с2	с1	с2
	f	x dx f x dx f x dx .
	с3	с3	с1
Откуда получим
с2	с2	с1	с3	с2
f x dx f x dx f x dx f				x dx f	x dx .
с1	с3	с3	с1	с3

6.(Оценка знака 1)

Пусть x a,b ,	a b	f (x) 0 . Тогда
		b
		f (x)dx 0 .
		a

7.(Оценка знака 2)

Пусть x a,b ,	a b	f (x) 0 . Тогда
		b
		f (x)dx 0 .

8.(Интеграл от нечетной функции на отрезке a, a )

Стаценко И.В. Лекция 1. Определенный интеграл.

Пусть f x f x . Тогда

f (x)dx 0 .

9.(Интеграл от четной функции на отрезке a, a )

Пусть f x f x . Тогда

a a

f (x)dx 2 f (x)dx .

10.(Оценка модуля)

Пусть функция f (x) интегрируема на отрезке a,b									a b . Тогда
			b		b
			b		b
		f (x)dx						dx .
		f (x)dx				f (x)		dx .
			a		a
11. (Оценка снизу и сверху)
Пусть x a,b			m f (x) M ,					m, M const .
Тогда
			b
m b a f				x dx M b a .
			a
Доказательство:
Из условия x a,b	m f (x) M следует, что
	b		b				b
	mdx f x dx Mdx .
	a		a				a
Откуда по свойству 4
	b		b					b
	m dx f x dx M dx .
	a		a					a
Откуда по свойству 3

m b a f x dx M b a .

12.(Оценка в среднем)

Стаценко И.В. Лекция 1. Определенный интеграл.

		10
Пусть x a,b	m f (x) M ,	m, M const .
Тогда m, M , m M :

f x dx b a .

Доказательство: Из доказанного неравенства:

					b
		m b a f x dx M b a ,
					a
следует, что
				b
				f x dx
			m	a		M .
			m			M .
					b a
	b
	f x dx				m, M ,
Пусть	a		, тогда				m M :
Пусть			, тогда				m M :
		b a

f x dx b a .

13.(Теорема о среднем)

Если функция f (x) непрерывна на отрезке				a,b , то на данном отрезке
найдется точка	, такая что
	b
	f x dx f b a .
	a
Доказательство:	по теореме Вейерштрасса функция, непрерывная на отрезке,
достигает на данном отрезке своего наименьшего				m и наибольшего значения
M , т.е.
	x a,b	m f (x) M ,	m, M const .

Стаценко И.В. Лекция 1. Определенный интеграл.

1 / 21 2 > Следующая >>>

Соседние файлы в папке Лекции

#
16.05.2024472.48 Кб0Лекция 1.pdf
#
16.05.2024458.2 Кб1Лекция 10.pdf
#
16.05.2024430.88 Кб2Лекция 11.pdf
#
16.05.2024449.15 Кб1Лекция 12.pdf
#
16.05.2024456.02 Кб0Лекция 13.pdf
#
16.05.2024416.26 Кб0Лекция 14.pdf