Добавил:

Chupapi_Munyanya Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МЭИ»

Предмет:

Высшая математика

Файл:

Лекция 11

.pdf

Скачиваний:

Добавлен:

16.05.2024

Размер:

483.36 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

Лекция 11. Условия возрастания и убывания функции в точке и на отрезке. Локальный экстремум. Необходимое условие локального экстремума. Достаточное условие экстремума. Наибольшее и наименьшее значение функции на отрезке.

Лекция 11

ИССЛЕДОВАНИЕ ФУНКЦИИ

1. Условия возрастания и убывания функции в точке и на отрезке

Теорема 1. (Достаточные условия строгой монотонности функции в точке)

Пусть
1. Функция		f (x) дифференцируема некоторой O x0 .
Тогда,	если	f (x0 ) 0 , то функция	f (x) возрастает в точке x0 ;
	если	f (x0 ) 0 , то функция	f (x) убывает в точке x0 .
Доказательство: (для случая f (x0 ) 0 )
В	некоторой достаточно малой O x0			зададим правое и левое
приращение функции в виде:

x x x ,

x x

x x x ,

x x .

Рассмотрим

f x0 0

lim

f x0 x f x0

lim

x 0

f x0 0

lim

f x0 x f x0

lim

x 0

Так как f (x0 ) 0

в некоторой O x0 , то возможны две ситуации:

f x0 0 0,

если

f 0 .

(1)

(2)

(3)

(4)

(5)

Стаценко И.В. Лекция 11. Математический анализ.

	2
f x0 0 0 ,	если x 0 ,	f 0 .	(6)
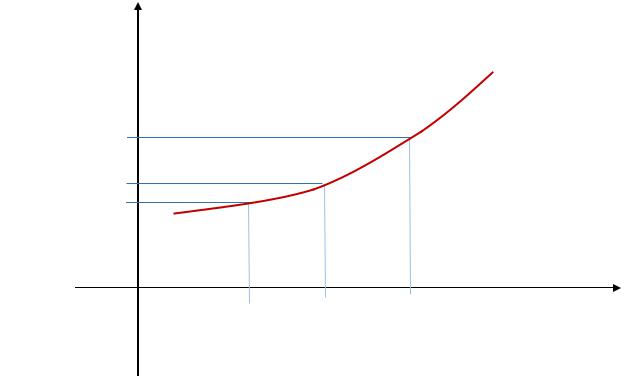
Тогда функция f (x) в некоторой окрестности точки		x0 имеет вид монотонно
возрастающей функции (см. рис.1)

f (x0 x )

f (x0 )

f (x0 x )

x x	x0	x0 x
0

Рис.1.

То есть, если в некоторой O x0

f (x0 ) 0 , то функция монотонно

возрастает в данной окрестности точки x0 .

Доказательство: (для случая

f (x0 ) 0 )

В некоторой достаточно малой O x0

зададим правое и левое приращение

функции в виде:

x x

(7)

x x x

x x .

(8)

Рассмотрим

f x0 0 lim

f x0 x

f x0

lim

(9)

x 0

Стаценко И.В. Лекция 11. Математический анализ.

			3
f x0 0	lim	f x0	x f x0			lim	f	.	(10)
			x
	x 0					x 0 x
Так как f (x0 ) 0	в некоторой O x0 , то возможны две ситуации:
	f x0 0 0 ,		если	x	0,	f 0 .			(11)
f x0 0 0 ,			если	x 0 ,		f	0 .		(12)
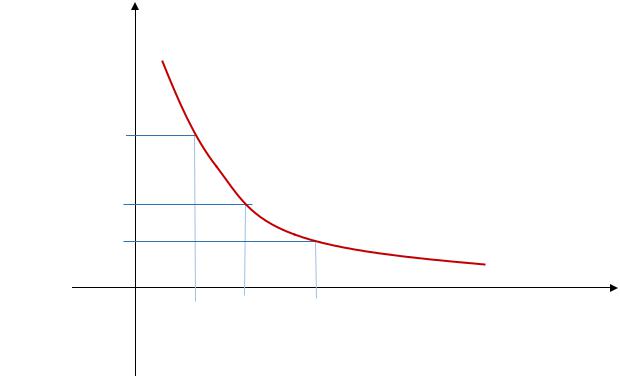
Тогда функция f (x) в некоторой окрестности точки x0							имеет вид монотонно
убывающей функции (см. рис.2)

f (x0 x )

f (x0 )

f (x x )
0					x
					x

x x	x	0	x0 x
0		0
				Рис.2.
То есть, если в некоторой O x0				f (x0 ) 0 , то функция монотонно

убывает в данной окрестности точки x0 .

Стаценко И.В. Лекция 11. Математический анализ.

Теорема 2. (Необходимые и достаточные условия нестрогой монотонности функции на отрезке)

Пусть

1.Функция f (x) непрерывна для x a,b .

2.Функция f (x) дифференцируема для x a,b .

Тогда, для того, чтобы функция f (x) была неубывающей (невозрастающей) наa,b необходимо и достаточно, чтобы f (x) 0 f (x) 0 x a,b .

Доказательство: (необходимость на примере неубывающей функции)

Пусть

f (x)

неубывающая

функция на

a,b ,

тогда

из

x2 x1

: x2 , x1 a,b следует, что f x2 f x1 .

Тогда в любой точке x0 a,b

f x0 0

lim

x0 x f x0

lim

x 0

так как

f 0 .

f x0 0

lim

f x0 x f x0

lim

x 0

так как

x 0 ,

f 0 .

Доказательство: (достаточность на примере неубывающей функции)

условия

(13)

(13’)

Пусть f (x) 0 для x a,b .

Тогда в любой точке x0 a,b

f x0 0

lim

x0 x f x0

lim

(14)

x 0

Откуда следует, что

f 0 ,

так как

x 0.

Тогда из условия x x0 : x, x0 a,b

следует,

что

f x f x0 . То есть в

данной окрестности функция является неубывающей.

Стаценко И.В. Лекция 11. Математический анализ.

Кроме того, в любой точке x0		a,b
f x0 0 lim	f	x0 x f x0		lim	f	0	,	(14’)
		x			x
x 0				x 0
Откуда следует, что f 0 , так как			x 0 .
Тогда из условия x x0 : x, x0 a,b			следует,	что f x f x0 . То есть в
данной окрестности функция является неубывающей.

Теорема 3. (Достаточные условия строгой монотонности функции на отрезке)

Пусть
1.Функция	f (x) непрерывна для x a,b .
2.Функция	f (x) дифференцируема для x a,b .
Тогда, если f (x) 0		f (x) 0 x a, b , то функция f (x) возрастает
(убывает) на a,b .

Доказательство аналогично представленному в теореме 2.

Замечание: В обратную сторону (необходимость) теорема не “работает”, так как не для всякой строго монотонной функции на отрезке a,b производная во всех

точках интервала a,b будет строго больше или строго меньше нуля.

Пример 1. Функция f (x) x3		на отрезке a, a строго возрастает, однако, в
точке x0 0	f (x0 ) 0 .

Стаценко И.В. Лекция 11. Математический анализ.

	6
	2. Экстремумы функции
Пусть функция	f (x) непрерывна некоторой O x0 .
Определение 1. Точка	x0 называется точкой строгого локального	максимума
функции f (x) , если
0 : x x0 f x0 f x .		(15)

Обозначения точки x0 и значения функции, в которой имеет место локальный максимум функции:

x0 xmax ,	(16)
xmax arg max f (x) ,	(17)
fmax f xmax .	(18)
Определение 2. Точка x0 называется точкой строгого локального	минимума
функции f (x) , если
0 : x x0 f x0 f x .	(19)

Обозначения точки x0 и значения функции, в которой имеет место локальный максимум функции:

x0 xmin ,		(20)
xmin arg min f (x) .		(21)
fmin	f xmin .	(22)
Точки строгого экстремума,	введенные согласно	определениям 1 и 2

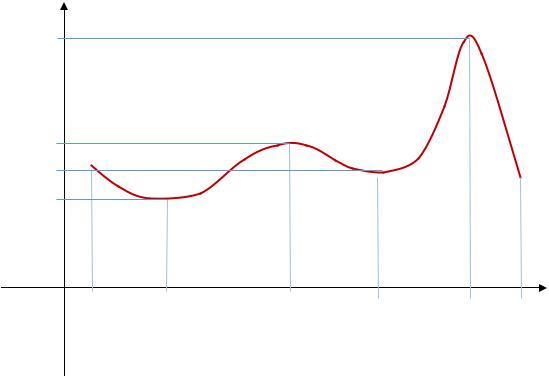
имеют локальный (не глобальный) характер, так как определяются в качестве экстремумов в рамках некоторой достаточно малой окрестности. На рис. 3.

представлена функция, имеющая на отрезке a,b несколько локальных минимумов и максимумов.

Стаценко И.В. Лекция 11. Математический анализ.

fmax 2
fmax1
fmin 2
fmin1
					x
a
a	xmin1	xmax1	xmin 2	xmax 2	b
	xmin1	xmax1	xmin 2	xmax 2	b
		Рис.3.
		Рис.3.

На данном рисунке имеется четыре локальных экстремума и два глобальных для данной функции на отрезке a,b экстремума: xmin1 и xmax 2 .

3. Необходимое и достаточное условие экстремума функции

Пусть функция f (x) непрерывна некоторой O x0 .

Теорема 4. (Необходимое условие экстремума)

Если точка x0 - точка экстремума функции f (x) , то в этой точке производная функции f (x) либо равна нулю, либо не существует.

Доказательство:

1. Пусть функция f (x) дифференцируема некоторой O x0 .

Если точка x0 xmax , то

Стаценко И.В. Лекция 11. Математический анализ.

f x0 0	lim	f	x0 x	f x0	lim	f	0 .	(23)
			x			x
	x 0				x 0
f x0 0	lim	f	x0 x f x0		lim	f	0 .	(24)
			x			x
	x 0				x 0
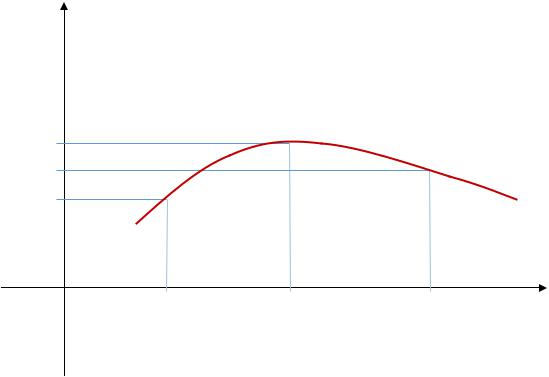
Так как в некоторой O x0 O xmax возможны две ситуации: (см. рис.4)
	при		x 0,	f 0 .				(25)
	при		x 0 ,	f 0 .				(26)

fmax

x x	xmax	x x
max		max

Рис.4.

Таким образом, при переходе через точку x0 xmax , производная функции f (x) меняет знак с плюса на минус. Следовательно, в точке x0 xmax производная функции f (x) равна нулю.

Стаценко И.В. Лекция 11. Математический анализ.

	9
2. Пусть функция f (x) дифференцируема некоторой O x0 .
Если точка x0 xmin , то
f x0 0 lim	f x0 x f x0	lim	f	0 .	(27)
	x		x
x 0		x 0
f x0 0 lim	f x0 x f x0	lim	f	0 .	(28)
	x		x
x 0		x 0
Так как в некоторой O x0	O xmin возможны две ситуации: (см. рис.4)

при x 0, f

при x 0 , f

0 .	(29)
0 .	(30)

fmin

x x	xmin	x x
min		min

Рис.5.

Стаценко И.В. Лекция 11. Математический анализ.

Таким образом, при переходе через точку x0 xmin ,

производная функции

f (x) меняет знак

минуса

на

плюс.

Следовательно,

точке

x0 xmin производная функции

f (x) равна нулю.

3. Пусть функция f (x) не дифференцируема некоторой O x0 .

Если

точка

- точка экстремума, то в данной ситуации для не

дифференцируемой

функции

O x0 можно только утверждать,

что

производная в точке x0

не существует.

В качестве

примеров

таких

ситуаций

можно

рассмотреть

функции

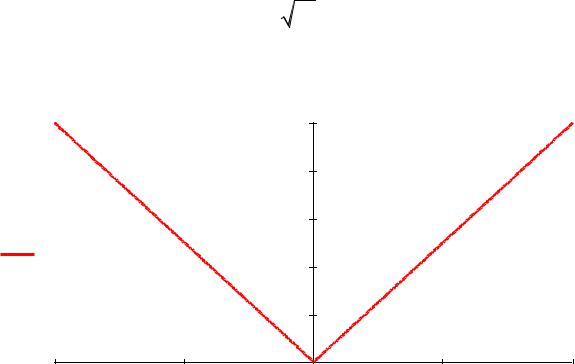
f (x) 3

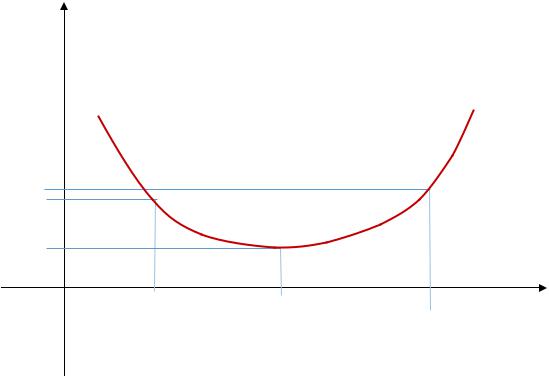
f (x)

см. рис.

см. рис. 7. У данных функций имеются

минимумы в точках x0

0, при этом производные в этих точках не существуют.

f ( x)

10	5	0	5	10
		x

Рис.6.

Стаценко И.В. Лекция 11. Математический анализ.

1 / 21 2 > Следующая >>>

Соседние файлы в папке Лекции

#
16.05.2024655.94 Кб2Лекция 1.pdf
#
16.05.2024484.06 Кб3Лекция 10.pdf
#
16.05.2024483.36 Кб1Лекция 11.pdf
#
16.05.2024477.32 Кб1Лекция 12.pdf
#
16.05.2024265.24 Кб1Лекция 13.pdf
#
16.05.2024278.18 Кб1Лекция 14.pdf
#
16.05.2024394.75 Кб1Лекция 15.pdf
#
16.05.2024391.73 Кб1Лекция 16.pdf