ЛЕКЦИЯ 14

РЕШЕНИЕ ЗАДАЧ МАТЕМАТИЧЕСКОЙ ФИЗИКИ.

Литература к лекции. Казенкин К.O., Амосова О.А.. Численное решение задач математической физики. Стационарные уравнения .М: Изд-во МЭИ, 2017.

§ 14.1. Двумерная задача Дирихле для уравнения Пуассона.

Рассмотрим уравнение Пуассона в прямоугольнике

(14.1)

относительно неизвестной функции ; функцию в правой части считаем известной. Дополним уравнение (14.1) граничным условием первого рода

(14.2)

Задача (14.1), (14.2) называется задачей Дирихле для уравнения Пуассона.

Здесь , ℾ - граница области.

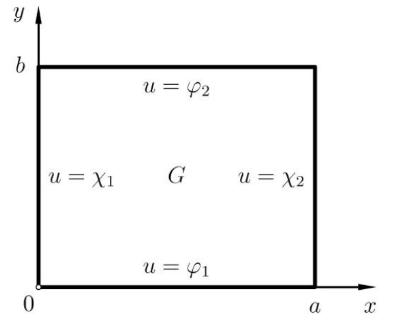
Далее, будем считать область G – прямоугольником: G=[0,a]x[0,b].

Тогда граничное условие нужно переписать в виде 4-х равенств:

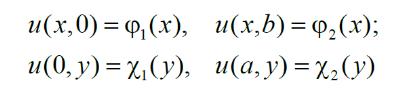
Введем на отрезках [0,a] и [0,b] сетки, состоящие из точек ,

i=0… и , j =0… . Для аппроксимации уравнения (14.1) возьмем пятиточечный шаблон, показанный на рисунке

В каждой точке построим разностное уравнение

(14.3)

где сеточная функция аппроксимирует функцию в правой части уравнения (14.1). В случае, если эта функция непрерывна, то можно положить . В развернутом виде уравнение (14.3) имеет вид

(14.4)

Аналогом граничных условий (14.2) являются уравнения

(14.5)

Рассмотрим на примере, что представляет собой РС (14.4)-(14.5).

ПРИМЕР 1. Построим систему сеточных уравнений для такой задачи.

, , ,

Очевидно, что решением такой задачи является функция

Возьмем квадрат [0,1]х[0,1] и разделим отрезки по x и y на 4 части

Для точки (1) :

Для точки (2) :

Для точки (3) :

Для точки (4) :

Для точки (5) :

И т.д.

Преобразуем 1-ое уравнение:

Преобразуем 2-ое уравнение:

Преобразуем 3-ое уравнение

Таким образом, получили систему уравнений Аu=b.

Матрица системы СЛАУ явяется пятидигональной, разреженной матрицей системы. Для такой матрицы нет эффективных прямых методов решения,

поэтому такие системы решают итерационными методами.

Система линейных уравнений с такой матрицей легко приводится к виду, удобному для итераций.

Метод простой итерации.

Приведем систему к виду, удобному для итераций.

Для этого систему Ax=b приведем к эквивалентному виду x=Bx+c.

Будем предполагать, что все диагональные элементы ненулевые. Выразим из 1-го уравнения , из второго ,…из последнего .

Введем матрицу B и вектор c :

, , , i,j=1,…m

Теперь система приведена к виду: x=Bx+c. Это преобразование называется преобразованием Якоби. Будем проводить итерации по формуле:

Формула называется расчетной формулой метода простой итерации.

Выберем начальное приближение . Подставим его в правую часть системы . Получим вектор , называемый первым приближением к корню. затем получим вектор и т.д. Запишем метод в покоординатной форме:

Теорема (достаточное условие сходимости метода) . Пусть выполнено условие:

(14.6)

Тогда при произвольном начальном приближении метод простой итерации сходится и справедливы оценки:

Метод Зейделя можно рассматривать как модификацию метода Якоби. Основная идея состоит в том, чтобы при вычислении очередного n+1 приближения к неизвестному при i>1 используют уже найденные (n+1) приближения к неизвестным , , … .

,где:

,

Тогда расчетные формулы метода Зейделя можно записать в таком виде:

В покоординатной форме метод Зейделя выглядит так:

Метод релаксации- модификация метода Зейделя.

Делают шаг по методу Зейделя:

А затем смещают компоненту на величину: , где - параметром релаксации.

Таким образом, новая компонента считается по формуле:

Метод релаксации можно записать в матричной форме записи:

При метод релаксации совпадает с методом Зейделя. При его называли методом верхней релаксации, при - методом нижней релаксации. Сейчас метод принято называть SOR- методом.

Применяется метод в основном для симметричных положительно определенных матриц.

Для рассмотренной задачи матрица B имеет вид:

В данной матрице условие сходимости не выполнено. Кроме того, при большой размерности методы простой итерации и Зейделя сходятся очень медленно. Поэтому реализуется итерационные методы в двумерном случае немного иначе.

1. Метод Якоби (простой итерации). Этот и подобные методы часто удобно записывать в следующем виде, просто дописывая номера итераций в уравнении (14.4):

(14.7)

откуда получаем простые для программирования расчетные формулы:

где , , .

Заметим, что в методе Якоби порядок вычисления величин не существен. Это следствие того, что метод является явным.

2. Метод Зейделя. В методе при вычислении очередного приближения к значения с индексами и будут известными (уже вычислены или являются граничными условиями), а значения с индексами и берем с предыдущей итерации. Поэтому имеем следующую запись метода Зейделя:

(14.8)

Расчетные формулы для программирования:

где выражения для , и приведены выше , а вычисления ведутся в указанном выше порядке.

4. Вычисление норм решения. Применение итерационных методов связано с вычислением апостериорной оценки разности приближений . Значения приближений естественным образом структурированы в виде двумерного массива. Однако поскольку в вычислениях они участвуют фактически в виде одномерного массива, как показано в пп. 2 и 3, наиболее употребительные нормы , и определим формулами, аналогичными нормам векторов

Заметим, что для задачи Дирихле разности элементов решения, соответствующих краевым условиям, равны нулю.