
ЛЕКЦИЯ 9.
РЕШЕНИЕ ДВУХТОЧЕЧНЫХ КРАЕВЫХ ЗАДАЧ
§ 9.1 СХОДИМОСТЬ РАЗНОСТНОЙ СХЕМЫ
Материал также изложен в учебнике §15.2, §15.3.
Напомним, что в лекции 8 рассматривался вопрос о решении краевой задачи:
найти
функцию
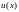 ,
удовлетворяющую дифференциальному
уравнению второго порядка внутри отрезка
,
удовлетворяющую дифференциальному
уравнению второго порядка внутри отрезка
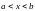 и дополнительным (граничным) условиям
в концах отрезка:
и дополнительным (граничным) условиям
в концах отрезка:
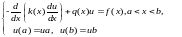 (9.1)
(9.1)
Были сформулированы основные теоремы о разрешимости и устойчивости задачи.
Теперь рассмотрим аналоги этих теорем для дискретной задачи – так называемой разностной схемы.
Для простоты рассматривается случай, когда коэффициент теплопроводности
k(x)=1.
Приведем разностную задачу для задачи (9.1) и будем ссылаться на нее
как на задачу (9.2).
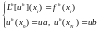 (9.2)
(9.2)
где
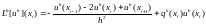 ,
,
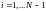
ТЕОРЕМА 9.1. Решение разностной схемы (9.2) существует и единственно.
Было доказано в лекции 8.
ТЕОРЕМА 9.2 (принцип максимума для
разностной схемы) . Пусть сеточная
функция
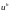 является решением разностной схемы
(9.2). Тогда если
является решением разностной схемы
(9.2). Тогда если
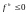 ,
,
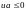 ,
,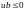 ,
то и
,
то и
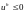 .
.
ТЕОРЕМА 9.3(априорная оценка решения). Для решения разностной схемы (9.2) справедлива априорная оценка:
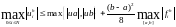 (9.3)
(9.3)
Пусть
- решение дифференциального уравнения
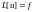 .
.
Определение.
Назовем сеточную функцию
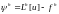 погрешностью аппроксимации разностного
уравнения
погрешностью аппроксимации разностного
уравнения
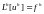 ,
,
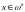 (9.4)
(9.4)
Подчеркнем,
что сеточная функция
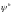 определяется в узлах сетки как разность
между
определяется в узлах сетки как разность
между
правой
и левой частью уравнения при подстановке
точного решения u
в уравнение (9.2) . Из определения
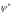 следует, что справедливо равенство:
следует, что справедливо равенство:
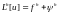 ,
,
означающее, что функция u удовлетворяет разностному уравнению (9.2) с точностью до погрешности аппроксимации.
Определение.
Будем говорить, что разностное
уравнение (9.2) аппроксимирует
дифференциальное уравнение
с m-м порядком (m>0),
если
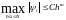 .
.
ТЕОРЕМА 9.4. (оценка погрешности аппроксимации). Пусть коэффициенты q и f дважды непрерывно дифференцируемы на отрезке [a,b]. Тогда дифференциальное уравнение аппроксимирует разностное со вторым порядком точности по h. При этом справедлива оценка:
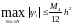 ,
,
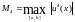 (9.5)
(9.5)
Доказательство:
В силу предположения о q
и f функция u(x)
имеет на отрезке [a,b]
непрерывную производную
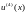 (см. теорему 8.1.) В силу определения
погрешности аппроксимации имеем:
(см. теорему 8.1.) В силу определения
погрешности аппроксимации имеем:
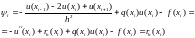
где
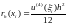 - погрешность аппроксимации производной
- погрешность аппроксимации производной
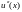 ее разностным аналогом. Окончательно,
ее разностным аналогом. Окончательно,
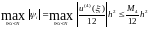 (9.6)
(9.6)
ч.т.д.
Рассмотрим вопрос об устойчивости разностной схемы. Наряду с исходной разностной схемой рассмотрим «возмущенную задачу»:
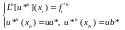
где
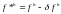 ,
,
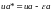 ,
,
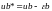 .
.
Определение. Будем называть разностную схему устойчивой, если справедлива оценка:
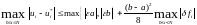 (9.7)
(9.7)
ТЕОРЕМА 9. 5. (устойчивость р. с.) Разностная схема устойчива.
Доказательство.
Заметим, что сеточная функция
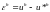 является решением разностной схемы:
является решением разностной схемы:
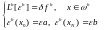
Применим к задаче априорную оценку (9.3), тогда получим оценку (9.7).
ч.т.д.
Дадим базовое определение сходимости разностной схемы.
Определение.
Будем называть погрешностью разностной
схемы сеточную функцию
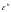 ,
принимающую значения
,
принимающую значения
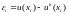 в узлах сетки
в узлах сетки
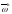 .
.
Определение.
Будем говорить, что разностная
схема сходится при
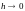 ,
если
,
если
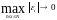 и
сходится с m-м порядком
точности по h если
и
сходится с m-м порядком
точности по h если
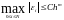 .
.
где C – некоторая постоянная, не зависящая от h.
ТЕОРЕМА 9.6 (сходимость р.с.) Пусть коэффициенты q и f дважды непрерывно дифференцируемы на отрезке [a,b]. Тогда разностная схема сходится со вторым порядком точности по h. При этом справедлива оценка:
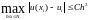 , (9.8)
, (9.8)
где
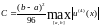
Доказательство.
Введем сеточную функцию
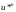 ,
значения которой в узлах сетки совпадают
с точными значениями решения краевой
задачи:
,
значения которой в узлах сетки совпадают
с точными значениями решения краевой
задачи:
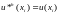 .
Тогда функция
является решением следующей задачи:
.
Тогда функция
является решением следующей задачи:
,
где
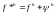 ,
,
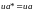 ,
,
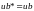 .
.
В силу теоремы об устойчивости (9.5) справедлива оценка (9.7):
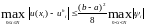
Применяя теорему об аппроксимации разностной схемы и оценку (9.5), получим оценку (9.8).
Оценка погрешности по правилу Рунге. На практике чаще используются апостериорные оценки погрешности, использующие расчеты на сгущающихся сетках.
Пусть
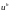 и
и
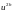 - решения разностной схемы, соответствующие
шагам h и 2h.
Тогда в соответствии с правилом Рунге
при определенных условиях справедлива
приближенная формула:
- решения разностной схемы, соответствующие
шагам h и 2h.
Тогда в соответствии с правилом Рунге
при определенных условиях справедлива
приближенная формула:
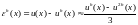 ,
,
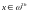 .
(9.10)
.
(9.10)
Формула
(9.10) применима только в узлах сетки
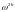 ,
то есть там, где определены обе сеточные
функции
и
.
,
то есть там, где определены обе сеточные
функции
и
.
§ 9.2 Построение разностных схем методом конечных разностей.
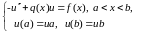 (9.11)
(9.11)
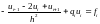 ,
i=1,
…N-1
,
i=1,
…N-1
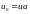
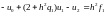
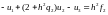
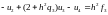 (9.12)
(9.12)
…..
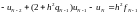
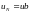
Введем матрицу системы и вектор правой части:
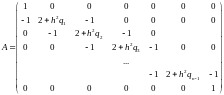 ,
,

Тогда систему можно записать в матричной форме: Au=f
Рассмотрим краевую задачу с более сложным дифференциальным уравнением:
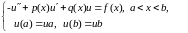
Метод конечных разностей состоит в замене производных их разностными аналогами.
A)
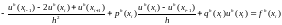 ,
i=1,..N-1
,
i=1,..N-1
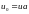 ,
,
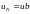 .
.
B)
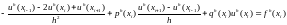 i=1,..N-1
i=1,..N-1
, .
Разница состоит в матрице системы уравнений и порядке аппроксимации схем.
Рассмотрим случай А) Перепишем систему . Сначала запишем уравнение так:
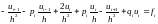
Затем соберем подобные члены:
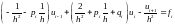
Тогда система уравнений будет выглядеть так:
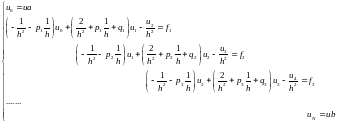
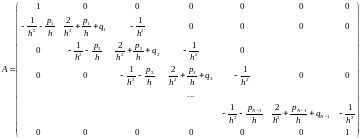
Вектор
f:
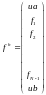
Для случая B) представим окончательный результат: Au=f
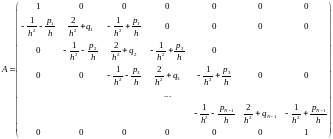
Вектор f остается без изменений. В случае B) cхема второго порядка аппроксимации.
§ 9.3. Материалы к ЛР 7.
Задача
7.1. Промоделировать распределение
температуры в стержне в зависимости
от входных параметров задачи.
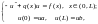 (7.1)
(7.1)
с
заданным шагом

ПОРЯДОК РЕШЕНИЯ ЗАДАЧИ
1. Найти аналитические решения задачи для случая входных данных (I) и (II). Записать полученные решения в таблицу (7.1).
2. Cоставить разностную схему для задачи (7.1). Предусмотреть решение системы разностных уравнений c помощью встроенной процедуры.
3.
Для случаев (I)
и (II)
построить графики аналитического
решения и приближенного, полученного
с шагом
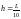 .
Найти величину погрешности по формуле
.
Найти величину погрешности по формуле
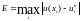 .
.
4.
Для случая 3 найти приближенные решения
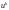 и
и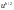 с шагами
и
с шагами
и
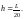 Построить точечный график приближенного
решения при
Найти погрешность по правилу Рунге.
Построить точечный график приближенного
решения при
Найти погрешность по правилу Рунге.
5. На одном чертеже построить графики всех полученных решений. Провести анализ погрешностей.
|
q |
f(x) |
Решение |
Погрешность |
(I) |
q(x)=0
|
f(x)=0 |
|
|
(II ) |
q(x)=0
|
f(x)=F(x) |
|
|
(III) |
q(x)= N |
f(x)=F(x) |
|
|
Рассмотрим случай (I)
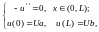 Решение:
Решение:
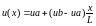
Рассмотрим случай (II)
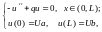 - однородное уравнение.
- однородное уравнение.
Составляем
характеристическое уравнение:
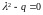 .
Корнями уравнения являются
.
Корнями уравнения являются
Значения
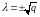 ,
Общим решением дифференциального
уравнения будет функция:
,
Общим решением дифференциального
уравнения будет функция:
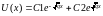 .
Для нахождения констант С1 и С2 воспользуемся
граничными условиями:
.
Для нахождения констант С1 и С2 воспользуемся
граничными условиями:
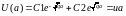
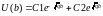 =ub
=ub
Решая систему уравнений, найдем коэффициенты С1 и С2.
Рассмотрим случай (III)
Если рассматривается неоднородное уравнение, то решить аналитически краевую задачу для произвольной правой части не удается. Будем решать ее численно.
Разностная схема для задачи готова – это СЛАУ ( 9.12). Остается найти решение СЛАУ.
Задача 7.2. Промоделировать распределение температуры в стержне в зависимости от входных параметров задачи.
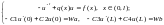 (7.2)
(7.2)
