4 семестр / Лекции / Лекция 6

ЛЕКЦИЯ 6. РЕШЕНИЕ ЗАДАЧИ КОШИ.

ЛИТЕРАТУРА. Учебник [1] Глава 14. §14.7, 14.10

§ 6.1 Методы Адамса.

В одношаговых методах, после того как найдено очередное значение , предыдущее значение отбрасывают и уже не используют в предыдущих вычислениях. В том случае, когда значение вычисляют с помощью k предыдущих значений , ,…, , метод называется k- шаговым. Наибольшее распространение получили k-шаговые методы Адамса.

Рассмотрим исходную задачу Коши:

при (6.1)

Введем равномерную сетку и проинтегрируем дифференциальное уравнение по отрезку :

(6.2)

Интеграл слева вычисляется без труда. Интеграл справа вычислить, вообще говоря, нельзя, так как в подинтегральную функцию входит неизвестная (искомая) функция y(t).

Основная идея построения методов Адамса состоит в следующем:

По известным вычисленным приближенным значениям решения , ,…, , вычислить значения функции в соответствующих точках: , ,…, , а затем выполнить аппроксимацию функции f(t,y) какой-либо легко интегрируемой функцией. Далее вычислить интеграл, стоящий в правой части и получить, таким образом, расчетную формулу.

Выделяют экстраполяционные методы Адамса (явные) и интерполяционные методы (неявные).

При построении экстраполяционных методов подинтегральная функция интерполируется по точкам , ,…, , далее эта функция интегрируется на отрезке , то есть выполняется экстраполирование. При этом получается такая расчетная формула:

При построении интерполяционных методов подинтегральная функция

интерполируется по точкам , ,…, . При вычислении интегралов получается расчетная формула :

Так как неизвестное входит и в левую часть и в правую, то получается неявный метод.

Построим простейшие формулы методов Адамса на основе интерполяции многочленами 1-ой степени.

Экстраполяционный метод Адамса.

Функцию на отрезке заменим многочленом первой степени. Для этого используем точки и . Тогда получим следующее :

Подставим в равенство ():

Таким образом, получили расчетную формулу Адамса-Башфорта:

(6.3)

Заметим, что метод получился явный, двухшаговый. Он требует для начала двух стартовых точек , .

Интерполяционный метод Адамса.

Функцию заменим многочленом первой степени, но на отрезке . Для этого используем точки и . Тогда получим следующее приближение :

Подставим в равенство ():

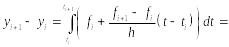
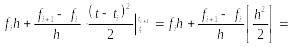
Таким образом, получили расчетную формулу Адамса-Моултона:

(6.4).

Заметим, что метод получился неявный, одношаговый. Он требует для начала только одной стартовой точки .

Справедлива следующая теорема

ТЕОРЕМА(без доказательства). Пусть решение задачи Коши y(t) непрерывно дифференцируемо k раз на отрезке . Тогда k- шаговый метод Адамса-Башфорта и (k-1) – шаговый метод Адамса-Моултона имеют порядок аппроксимации равный k.

ПРИМЕР 6.1. Найдем порядок аппроксимации метода Адамса-Башфорта. Для этого запишем формулу (6.3) в канонической форме и вычислим величину порядка аппроксимации, раскладывая соответствующие значения по формуле Тейлора:

Получили метод 2-го порядка аппроксимации.

Справедливо также следующее утверждение.

УТВЕРЖДЕНИЕ. Пусть выполнено условие 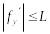. Тогда если k-шаговый метод Адамаса имеет p-ый порядок аппроксимации и начальные значения , ,…, определяются с p-ым порядком точности, то метод сходится также с p-ым порядком точности.

Приведем расчетные формулы методов Адамса-Башфорта и Адамса-Моултона 3-го порядка точности :

Может показаться, что при наличии явных формул Адамса высокого порядка точности нет необходимости в использовании неявных формул. Однако, на практике явные методы Адамса используются очень редко, так как неявные методы обладают лучшими свойствами устойчивости и позволяют вести расчет с существенно большими шагами, нежели явные методы. Чтобы избежать решения уравнений, применяют методы прогноза и коррекции.

Для методов Адамса используют для прогноза явные формулы Адамса-Башфорта, а затем для коррекции- неявные методы Адамса-Моултона. Например, для методов 3-его порядка будем иметь:

Прогноз:

Коррекция:

ПРИМЕР 6.2. Найдем решение задачи

1) методом 2 -го порядка точности Адамса-Башфорта

Метод требует двух стартовых точек:

Так как метод двухшаговый требуется найти 2 стартовые точки:

=1000, а вычислим точно, так как нам известно точное решение .

Итак,

2) метод Адамса-Моултона:

Метод одношаговый, но неявный. Для данного примера расчетная формула будет достаточно простой, так как правая часть уравнения линейна по y. Преобразуем ее так:

,

, ,

Заметим, что точное значение решения имеет вид:

, ,

t	0	0.1	0.2	0.3
Точное решение	1000	1002.0020013	1004.00801068	1006.01803605
Метод А-Б	1000	1002.0020013	1004.00800734	1006.01802936
		0	3.3х10^-6	6.7х10^-6
Метод А-М	1000	1002.002002	1004.00801135	1006.01803338
		6.7х10^-7	6.7х10^-7	2.7х10^-6

§ 6.2. Системы дифференциальных уравнений и уравнения высокого порядка.

Рассмотрим задачу Коши для системы уравнений первого порядка:

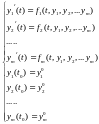(6.5)

Запишем систему в векторной форме:

, ,

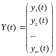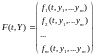Тогда задачу Коши (6.5) можно записать так:

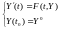
Рассмотренные методы применяются также и для систем ОДУ 1-го порядка и имеют векторную форму. Например, метод Эйлера:

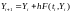
ПРИМЕР 6.3.

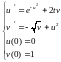
Сделаем один шаг по методу Эйлера:

,

,

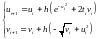
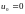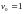
h=0.1

,

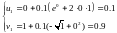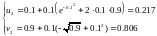
Получили решение в точках t=0, t=0.1 и t=0.2. В векторной форме:

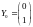
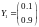
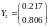
Уравнение m-го порядка.

Задача Коши для уравнения m-го порядка имеет вид:

,

, , …

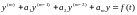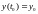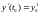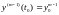
Сведем поставленную задачу к системе уравнений 1-го порядка. Для этого введем m функций:

…

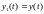
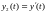
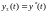
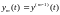
Тогда можно переформулировать задачу в новых переменных:

…

….

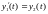
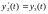
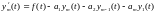
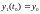
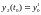
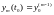
Если ввести векторы , ,

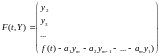
То задача сводится к системе ОДУ

При этом решением задачи является функция .

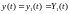Можно применять и методы Адамса.