
ЛЕКЦИЯ 4. РЕШЕНИЕ ЗАДАЧИ КОШИ.
ЛИТЕРАТУРА. Учебник [1] Глава 14. §14.1,14.2,14.3
§ 4.1 Постановка задачи Коши.
Пусть
дано ОДУ 1-го порядка. Требуется найти
функцию
 ,
удовлетворяющую дифференциальному
уравнению и начальному условию:
,
удовлетворяющую дифференциальному
уравнению и начальному условию:
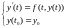 при
при
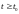 (4.1)
(4.1)
Геометрически
задача (4.1) состоит в нахождении
интегральной кривой, выходящей из точки
 ,
которая в каждой точке
,
которая в каждой точке
 имеет заданное направление касательной
имеет заданное направление касательной
 .
.
Пример 4.1. Рассмотрим простой пример.
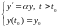 (4.2)
(4.2)
Решение задачи. Уравнение решается методом разделения переменных:
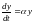 ,
,
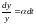 ,
,
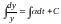 ,
,
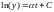 ,
,
 ,
,
 общее решение.
общее решение.
Подставляя
начальное условие, имеем:
 ,
,
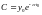 .
Окончательно,
.
Окончательно,

Конкретизируем задачу 4.2.
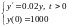
Решением
задачи является функция
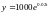
![]()
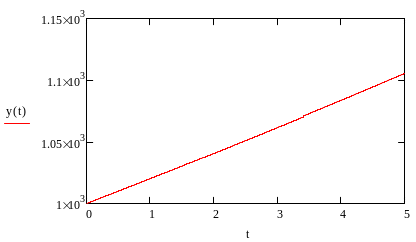
Можно
найти несколько значений функции:
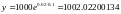

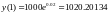
Как
правило, решение задачи будем искать
на конечном отрезке
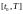 .
.
Обозначим
через
 и
будем называть это множество полосой.
и
будем называть это множество полосой.
Всюду далее предполагается, что функция является дифференцируемой достаточное количество раз. Сформулируем теорему о разрешимости задачи Коши.
Теорема
4.1. Пусть
функция
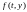 определена
и непрерывна в полосе
определена
и непрерывна в полосе
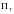 .
Предположим также, что
.
Предположим также, что
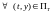 справедливо неравенство
справедливо неравенство
 .
Тогда для каждого начального значения
.
Тогда для каждого начального значения
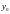 существует единственное решение
задачи Коши (4.1) , определенное на отрезке
.
Кроме того, если функция
существует единственное решение
задачи Коши (4.1) , определенное на отрезке
.
Кроме того, если функция
 непрерывно дифференцируема m
раз в полосе
,
то функция
непрерывно дифференцируема (m+1)
раз на этом отрезке.
непрерывно дифференцируема m
раз в полосе
,
то функция
непрерывно дифференцируема (m+1)
раз на этом отрезке.
§ 4.2. Дискретизация задачи коши. Методы Тейлора и Эйлера.
Заменим
отрезок
- область непрерывного изменения
аргумента t
множеством дискретных значений :
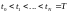 называется сеткой. Обозначим
называется сеткой. Обозначим
 - шаг сетки. Будем далее считать, что
сетка равномерная, то есть
- шаг сетки. Будем далее считать, что
сетка равномерная, то есть
 ,
,
 ,
,
 ,
i=0,1,
…N.
Точное
решение в точке
,
i=0,1,
…N.
Точное
решение в точке
 будем обозначать
будем обозначать
 ,
а приближенное решение в той же точке
будем обозначать через
,
а приближенное решение в той же точке
будем обозначать через
 .
Если важно указать с каким шагом вычислили
приближенное решение, то будем обозначать
.
Если важно указать с каким шагом вычислили
приближенное решение, то будем обозначать
 ..
..
Решением задачи Коши является таблица приближенных значений:
|
|
… |
|
|
|
|
|
|
|
Метод разложения по формуле Тейлора.
Воспользуемся разложением функции y(t) по формуле Тейлора:
 (4.3)
(4.3)
Здесь
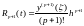 - остаточный член формулы Тейлора.
- остаточный член формулы Тейлора.
Если
значение решения y
в точке t
известно, то в силу уравнения (4.1)
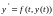 значение
производной также известно. Теперь
найдем производные
значение
производной также известно. Теперь
найдем производные
 ,
,
 ,
…
,
…

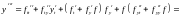
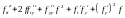 ,
,
И т.д.
Метод, основанный на удержании членов разложения до p-го порядка включительно, называется методом разложения по формуле Тейлора, p-го порядка.
Например, расчетная формула метода Тейлора 2-го порядка имеет вид:
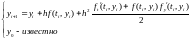
На практике метод применяется довольно редко, так как вычисление производных
высокого порядка является трудоемкой задачей.
Метод разложения по формуле Тейлора для ПРИМЕРА 4.1
Производные вычисляются просто:
 ,
,
 ,
,
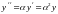 ,
,
 и т.д.
и т.д.
Следовательно, расчетная формула примет вид:
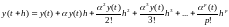
Для конкретного примера имеем:
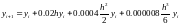
Возьмем шаг h=0.1:



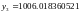
ПРИМЕР 4.2.
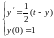
Выберем шаг h=0.2
Заметим, что производные можно вычислить по общей формуле

Или (что тоже самое):

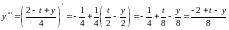
Таким образом, расчетная формула метода имеет вид:

Результаты расчетов:
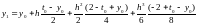 =
=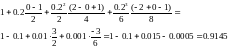
Значение получено. Найдем решение в следующей точке:
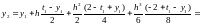
 =0.85617008
=0.85617008
В этой задаче можно найти точное решение. Рассмотрим дифференциальное уравнение
 и
найдем решение однородного уравнения:
и
найдем решение однородного уравнения:
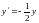 .
.
Разделяя
переменные, получим
 ,
откуда
,
откуда
 .Легко
проверить, что частным решением исходного
уравнения является функция
.Легко
проверить, что частным решением исходного
уравнения является функция
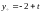 .
Тогда получили решение дифференциального
уравнения
.
Тогда получили решение дифференциального
уравнения
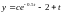 .
Подставляя начальное условие, найдем
константу с:
.
Подставляя начальное условие, найдем
константу с:

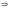


Вычислим значения точного решения в найденных точках: y(0.2)=0.91451225
y(0.4)=0.85619226
|
|
|
|
|
Точное решение |
1 |
0.91451225 |
0.85619226 |
0.82245466
|
метод Тейлора |
1 |
0.9145 |
0.85617008 |
0.82242456 |
Метод Эйлера.
Простейшим и исторически первым методом решения задачи Коши является метод Эйлера :
 (4.3)
(4.3)
Его можно получить, если в разложении по формуле Тейлора оставить всего 2 члена
разложения.
Геометрическая интерпретация состоит
в аппроксимации решения на шаге
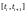 касательной
касательной
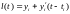 ,
проведенной в точке
,
проведенной в точке
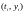 к
интегральной кривой y(t).
к
интегральной кривой y(t).
Метод Эйлера для примера 4.1.
Возьмем шаг h=0.1
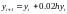
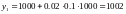


|
|
|
|
|
Точное решение |
1000 |
1002.00200134
|
1004.00801677 |
1006.018360541 |
Метод Тейлора |
1000 |
1002.0020013 |
1004.0090167 |
1006.018360521 |
Метод Эйлера |
1000 |
1002 |
1004.004 |
1006.012008 |
Рассмотрим решение задачи из ПРИМЕРА 4.1 методом Эйлера:
Выберем шаг h=0.2
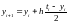
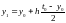 =
=
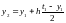 =
=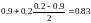
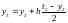 =
=
|
|
|
|
|
Точное решение |
1 |
0.91451225 |
0.85619226 |
0.82245466
|
Метод Эйлера |
1 |
0.9 |
0.83 |
0.787 |
ОПР.
Будем называть погрешностью сеточную
функцию
 со значениями в узлах
со значениями в узлах
 равными
равными
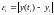
Напомним,
что
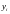 -
приближенное решение задачи, а
- точное решение задачи в точке
.
-
приближенное решение задачи, а
- точное решение задачи в точке
.
ОПР.
В качестве меры погрешности метода
примем величину
 .
.
ОПР.
Будем говорить, что метод сходится с
p-ым порядком
точности по h, если
справедливо неравенство:
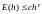 ,
где c – константа, не
зависящая от h.
,
где c – константа, не
зависящая от h.
Обычно в вычислениях величину называют погрешностью на шаге
и
обозначают через
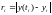 .
Величину
.
Величину
 называют глобальной погрешностью.
называют глобальной погрешностью.
Сведем результаты в единую таблицу:
|
|
|
|
|
Точное решение |
1 |
0.91451225 |
0.85619226 |
0.82245466
|
метод Тейлора |
1 |
0.9145 |
0.85617008 |
0.82242456 |
|
0 |
0.00001225 |
0.00002218 |
0.00003010 |
Метод Эйлера |
1 |
0.9 |
0.83 |
0.787 |
- погрешность на шаге метода Эйлера |
0 |
0.01451225 |
0.02619226 |
0.03545466 |
E(h)= 0.00003 для метода Тейлора
E(h)= 0.04 для метода Эйлера

Геометрическая интерпретация метода Эйлера.




З ная
(t1,y1),
можно аналогично получить новую точку
(t2,y2)
и т.д.
ная
(t1,y1),
можно аналогично получить новую точку
(t2,y2)
и т.д.
Из геометрической иллюстрации следует, что:
На каждом шаге есть погрешность (на рисунке это отрезок BD). Погрешность тем больше, чем больше шаг.
Ошибка может накапливаться.

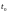





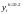
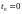
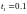
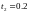



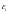 - погрешность на
шаге метода Тейлора
- погрешность на
шаге метода Тейлора