ДИСЦИПЛИНА МММФП (2 семестр)
Лекции - каждая неделя, ПЗ 1-ая неделя, ЛЗ 2-ая неделя,
РЗ - 7 задач, ЛР -4, экзамен. КМ- 5.
Литература.
1. Амосов А.А, Дубинский Ю.А., Копченова Н.В. Вычислительные методы. М: Издательский дом МЭИ, 2008.
2. Казенкин К.О. Указания к решению задач по вычислительной математике. Приближение функций. Численное интегрирование. Численное дифференцирование. М: Издательство МЭИ. 2011.
3.Казенкин К.О. Указания к решению задач по вычислительной математике. Численное решение задачи Коши. Численное решение двухточечной краевой задачи. М: Издательство МЭИ. 2014.
6.Казенкин К.О. Амосова О.А. Численное решение задач математической физики. Стационарные уравнения.
7 Амосова О.А., Вестфальский А.Е., Крупин Г.В. Упражнения по основам численных методов. М: Издательство МЭИ, 2016.
ЛЕКЦИЯ 1 . ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ
§ 1.1 Введение.
В прикладных задачах часто возникает необходимость вычисления определенного интеграла
.
В большинстве случаев получить значение интеграла по формуле Ньютона - Лейбница не удается. Обычно вычисление интеграла производится по формулам численного интегрирования, которые называются квадратурными формулами.
Пример
1.1.
Требуется вычислить интегральный синус
.Эта
функция часто используется в приложениях.
Рассмотрим способы вычисления интеграла в фиксированной точке x=1.
ПЕРВЫЙ
СПОСОБ.
Разложим подинтегральную функцию
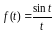в
ряд Тейлора в окрестности точки
.
Ряд
сходится быстро. Вычисление значения
функции
c
помощью 4-х слагаемых дает приближенное
значение 0.9460827664 . Таким образом,
получили 6 верных цифр.
ВТОРОЙ СПОСОБ РАССМОТРИМ НИЖЕ.
§1.2. Постановка задачи и простейшие формулы.
Постановка
задачи.
Дан определенный интеграл:
.
Требуется найти приближенное значение
интеграла
такое,
что
.
Ниже будет рассмотрен подход, основанный на интерполяции подинтегральной функции полиномом, интеграл от которого легко вычисляется.
Известно,
что определенный интеграл обладает
свойством линейности. Ясно, что приближать
функцию на всем отрезке [a,b]
методом глобальной интерполяции
неэффективно. Поэтому исходный отрезок
[a,b]
разбивают на элементарные отрезки
,
и тогда исходный интеграл будет
представлять собой сумму элементарных
интегралов:
(1.1)
Так как при интерполировании функции многочленом используются значения функции в узлах, то окончательно, формула примет вид:
(1.2)
Далее
точки
будем
называть узлами
квадратурной формулы (1.2),
- весами квадратурной формулы,
- остаточным членом квадратурной формулы.
При оценке эффективности формулы будем
исходить из того, что трудоемкой операцией
является вычисление функции в точке.
Итак,
разобьем отрезок на n
равных частей, тогда получим n
элементарных отрезков
,
и n+1
узел квадратуры, шаг интегрирования
при этом равен h=(b-a)/n
. Будем называть отрезок
- элементарным, а отрезок
- составным.
ФОРМУЛЫ ПРЯМОУГОЛЬНИКОВ
Элементарные
формулы прямоугольников получаются
при замене функции
на элементарном отрезке:
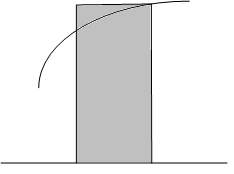
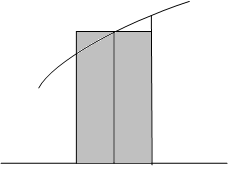
Составные формулы прямоугольников:
Пример 1.2. Вычисление значения определённого интеграла по формулам прямоугольников. Для упрощения ручных расчетов рассмотрим достаточно простую задачу.
Требуется вычислить:
Точное значение легко вычисляется по формуле Ньютона-Лейбница:
=
=
Для вычисления интеграла по квадратурной формуле необходимо выбрать число разбиений отрезка n.
Пусть,
например, n=5,
тогда
Расчет по формуле левых прямоугольников:
Погрешность
расчета
.
C
Суммарная площадь получилась меньше площади криволинейной трапеции.
Расчет по формуле правых прямоугольников:
Погрешность
расчета
Расчет по формуле центральных прямоугольников:
Погрешность
расчета
ВТОРОЙ СПОСОБ нахождения интегрального синуса.
Протабулируем
функцию
на отрезке [0,1] c
шагом 1/4.
t |
0 |
1/4 |
1/2 |
3/4 |
1 |
f(t) |
1 |
0.9896 |
0.9589 |
0.9089 |
0.8415 |
Применяем построенные формулы.
Левые прямоугольники
Правые прямоугольники
3. Центральные прямоугольники, но шаг в два раза больше!!
В первых двух случаях получили одну верную цифру, во втором – две.
ОЦЕНКИ ПОГРЕШНОСТЕЙ.
Выведем оценку погрешности, например, левых прямоугольников.
=
Определение.
Будем говорить, что формула имеет p-ый
порядок точности по h,
если справедлива оценка:
Таким образом, формула левых прямоугольников имеет первый порядок точности по h.
Аналогично доказывается, что формула правых прямоугольников имеет также первый порядок точности по h и аналогичную оценку погрешности.
Оценим погрешность формулы центральных прямоугольников:
Формула центральных прямоугольников имеет второй порядок точности по h.
ФОРМУЛА ТРАПЕЦИЙ
Приблизим функцию на элементарном отрезке полиномом 1-ой степени:
Тогда интегрируя многочлен, получим элементарную формулу трапеций:
Формула имеет простой геометрический смысл - площадь криволинейной трапеции заменяется площадью прямоугольной трапеции, равной полусумме оснований на высоту.
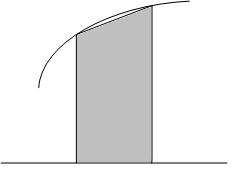
Составная формула трапеций получается суммированием элементарных интегралов:
Оценим величину погрешности с помощью остаточного члена интерполяции:
=
Окончательно, оценка погрешности имеет вид:
.
Формула трапеций имеет второй порядок точности по h.
ФОРМУЛА СИМПСОНА.
Элементарная формула Симпсона получается с использованием интерполяционного многочлена второй степени.
Интегрируя представленный многочлен, получим элементарную формулу Симпсона:
Геометрически формула получена при замене исходной функции на элементарном отрезке параболой.
Составная формула Симпсона:
ЗАДАНИЕ НА ДОМ: вывод формулы Симпсона.
Справедлива следующая теорема.
Теорема.
Пусть функция f(x)
имеет ограниченную четвертую производную
на
отрезке
.
Тогда для формулы Симпсона справедлива
априорная оценка:
ПРАВИЛО РУНГЕ
Правило двойного пересчета. Правило практической оценки погрешности.
Пусть - приближенное значение интеграла, вычисленное по некоторой квадратурной формуле. Для погрешности квадратурной формулы справедливо представление:
Где
и
- величины, не зависящие от h.Тогда
величина
называется
главным членом погрешности квадратурной
формулы. Отбросим члены более высокого
порядка малости, и будем считать, что
сделано два вычисления интеграла: с
шагом h
и h/2:
Вычитая из верхнего равенства нижнее, получим приближенное равенство:
Учитывая приближенное равенство (), можно считать, что выведена формула:
(1.3)
называемая правилом Рунге или апостериорной оценкой погрешности.
Уточнение по Рунге
Приближенное равенство (1.3) позволяет получить уточненное значение интеграла:
Последняя формула называется уточнением по Рунге.
Замечание 1. Заменой h на 2h формула (1.3) приводится к следующему виду:
Замечание 2. Выполнение уточнения по Рунге для формулы трапеций приводит к формуле, совпадающей с формулой Симпсона. Действительно,
ПРИМЕР.
Вычислить интеграл
по формуле трапеций.
Решение.
Вычислим значения подинтегральной функции в следующих точках:
f(0)=0.8 f(1/2)=1.414214-0.2=1.214214 f(1)=1.8
Продемонстрируем работу правила Рунге. Вычислим интеграл по формуле трапеций при уменьшенном вдвое шаге интегрирования.
-
погрешность уменьшилась примерно в 3
раза.
Замечание 3. Формулу Симпсона можно писать в целых индексах, если за шаг hпринять расстояние между узлами квадратурной формулы и ввести целую нумерацию узлов:
Число узлов должно быть равно 2n+1 , последний индекс четный.
Тогда формула примет вид:
Априорная оценка погрешности примет вид:
