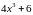Лабораторная работа 7. Численное решение стационарных задач теплопроводности
Задача
7.1.
Промоделировать распределение
температуры в стержне в зависимости
от входных параметров задачи.
(7.1)
с
заданным шагом
Порядок решения задачи
1. Найти аналитические решения задачи для случая входных данных (I) и (II). Записать полученные решения в таблицу (7.1).
2. Cоставить разностную схему для задачи (7.1). Предусмотреть решение системы разностных уравнений c помощью встроенной процедуры.
3.
Для случаев (I)
и (II)
построить графики аналитического
решения и приближенного, полученного
с шагом
.
Найти величину погрешности по формуле
.
4.
Для случая 3 найти приближенные решения
и
с шагами
и
Построить точечный график приближенного
решения при
Найти погрешность по правилу Рунге.
5. На одном чертеже построить графики всех полученных решений. Провести анализ погрешностей.
Табл.7.1
|
q |
f(x) |
Решение |
Погрешность |
(I) |
q(x)=0
|
f(x)=0 |
|
|
(II ) |
q(x)=0
|
f(x)=F(x) |
|
|
(III) |
q(x) |
f(x)=F(x) |
|
|
Задача 7.2. Промоделировать распределение температуры в стержне в зависимости от входных параметров задачи.
(7.2)
Порядок решения задачи
1. Cоставить разностную схему для задачи (7.2). Предусмотреть решение системы разностных уравнений c помощью метода прогонки.
2.
Найти приближенное решение задачи
(7.2) с точностью
.
Погрешность
находить по правилу Рунге.
3. Построить точечный график приближенного решения.
Приложение 7.A варианты заданий к лабораторной работе 7
ВНИМАНИЕ!
Номер варианта
для лабораторных работ вычисляется
по следующей формуле:
1)
для групп 9–11;
2) Для групп 12–15
(здесь
— номер группы, а
— индивидуальный номер студента по
журналу).
Примечание.
Если полученный номер
получился больше значения 50, то принять
Если
полученный номер
получился меньше 1, то принять
Таблица к задачам 7.1-7.2.
№ |
F(x) |
L |
ua |
ub |
q |
|
C1 |
C2 |
C3 |
C4 |
Wa |
Wb |
7.1.1 |
|
2 |
3 |
0 |
5 |
|
0 |
1 |
1 |
0 |
8 |
0 |
7.1.2 |
|
1 |
0 |
5 |
2 |
|
1 |
0 |
1 |
0 |
4 |
1 |
7.1.3 |
|
1 |
2 |
6 |
1.8 |
|
1 |
1 |
1 |
0 |
1 |
3 |
7.1.4 |
|
2 |
4 |
1 |
3.2 |
|
0 |
1 |
0 |
1 |
6 |
6 |
7.1.5 |
|
1 |
2 |
4 |
2.6 |
|
0 |
1 |
1 |
1 |
7 |
0 |
7.1.6 |
|
1 |
1 |
5 |
0.8 |
|
1 |
0 |
0 |
1 |
0.5 |
1.5 |
7.1.7 |
|
2 |
3 |
3 |
6 |
|
1 |
0 |
1 |
1 |
4 |
0 |
7.1.8 |
|
0.5 |
6 |
0.6 |
3 |
|
1 |
1 |
1 |
1 |
3.5 |
1 |
7.1.9 |
|
|
3 |
1 |
0.4 |
|
0 |
1 |
0 |
1 |
7 |
2 |
7.1.10 |
|
0.5 |
1 |
5 |
3 |
|
0 |
1 |
1 |
0 |
8 |
0 |
7.1.11 |
|
|
2 |
1 |
2.5 |
|
0 |
1 |
1 |
1 |
4 |
1 |
7.1.12 |
|
1 |
3 |
3 |
1.8 |
|
1 |
0 |
0 |
1 |
1 |
3 |
7.1.13 |
|
1 |
-2 |
2 |
4.2 |
|
1 |
0 |
1 |
0 |
6 |
6 |
7.1.14 |
|
1 |
2 |
-2 |
3.6 |
|
1 |
1 |
1 |
1 |
7 |
0 |
7.1.15 |
|
1.5 |
3 |
-3 |
4 |
|
0 |
1 |
1 |
0 |
0.5 |
1.5 |
7.1.16 |
|
3 |
5 |
0 |
6 |
|
1 |
0 |
1 |
0 |
4 |
0 |
7.1.17 |
|
1 |
0 |
2 |
3 |
|
1 |
1 |
1 |
0 |
3.5 |
1 |
7.1.18 |
|
1 |
2 |
6 |
0.4 |
|
0 |
1 |
0 |
1 |
7 |
2 |
7.1.19 |
|
2 |
4 |
2 |
2.5 |
|
0 |
1 |
1 |
1 |
8 |
0 |
7.1.20 |
+3 |
1 |
3 |
-3 |
0.8 |
|
1 |
0 |
0 |
1 |
4 |
1 |
7.1.21 |
|
1 |
1 |
3 |
0.7 |
|
1 |
0 |
1 |
1 |
1 |
3 |
7.1.22 |
|
2 |
-3 |
3 |
4.2 |
|
1 |
1 |
1 |
1 |
6 |
6 |
7.1.23 |
|
0.5 |
2 |
0.2 |
2.7 |
|
0 |
1 |
0 |
1 |
7 |
0 |
7.1.24 |
|
1 |
3 |
-1 |
3.8 |
|
0 |
1 |
1 |
0 |
0.5 |
1.5 |
7.1.25 |
|
0.5 |
1 |
5 |
6 |
|
0 |
1 |
1 |
1 |
4 |
0 |
7.1.26 |
|
1 |
3 |
0 |
3 |
|
1 |
0 |
0 |
1 |
3.5 |
1 |
7.1.27 |
|
2 |
-2 |
-4 |
0.4 |
|
1 |
0 |
1 |
0 |
7 |
2 |
7.1.28 |
|
1.5 |
2 |
6 |
3 |
|
0 |
1 |
1 |
0 |
8 |
0 |
7.1.29 |
|
1 |
4 |
1 |
4 |
|
1 |
0 |
1 |
0 |
4 |
1 |
7.1.30 |
|
1 |
-1 |
4 |
1.5 |
|
1 |
1 |
1 |
0 |
1 |
3 |
7.1.31 |
|
2 |
-1 |
1 |
2.6 |
|
0 |
1 |
0 |
1 |
6 |
6 |
7.1.32 |
|
|
3 |
3 |
3 |
|
0 |
1 |
1 |
1 |
8 |
0 |
7.1.33 |
|
0.5 |
1 |
1 |
1 |
|
1 |
0 |
0 |
1 |
4 |
1 |
7.1.34 |
|
|
2 |
2 |
2 |
|
1 |
0 |
1 |
1 |
1 |
3 |
7.1.35 |
|
|
-1 |
-1 |
4 |
|
1 |
1 |
1 |
1 |
6 |
6 |
7.1.36 |
|
0.3 |
3 |
1 |
3 |
|
0 |
1 |
0 |
1 |
7 |
0 |
7.1.37 |
|
2 |
-4 |
2 |
1.4 |
|
0 |
1 |
1 |
0 |
0.5 |
1.5 |
7.1.38 |
|
1.2 |
-4 |
1 |
1.4 |
|
0 |
1 |
1 |
1 |
4 |
0 |
7.1.39 |
|
0.5 |
1 |
1 |
1 |
|
1 |
0 |
0 |
1 |
3.5 |
1 |
7.1.40 |
|
0.3 |
3 |
1 |
3.3 |
|
1 |
0 |
1 |
0 |
7 |
2 |
7.1.41 |
|
1 |
3 |
0 |
3 |
|
1 |
1 |
1 |
1 |
8 |
0 |
7.1.42 |
|
1 |
2 |
-4 |
2.3 |
|
0 |
1 |
1 |
0 |
4 |
1 |
7.1.43 |
|
1.5 |
2 |
5 |
2.5 |
|
1 |
0 |
1 |
0 |
1 |
3 |
7.1.44 |
|
1 |
4 |
2 |
4.6 |
|
1 |
1 |
1 |
0 |
6 |
6 |
7.1.45 |
|
1 |
-1 |
5 |
1.8 |
|
0 |
1 |
0 |
1 |
8 |
0 |
7.1.46 |
|
2 |
-2 |
1 |
2 |
|
0 |
1 |
1 |
1 |
4 |
1 |
7.1.47 |
|
|
3 |
3 |
3.4 |
|
1 |
0 |
0 |
1 |
1 |
3 |
7.1.48 |
|
0.5 |
1 |
-1 |
1.6 |
|
1 |
0 |
1 |
1 |
6 |
6 |
7.1.49 |
|
|
2 |
2 |
2.4 |
|
1 |
1 |
1 |
1 |
7 |
0 |
7.1.50 |
|
|
-1 |
-1 |
1.4 |
|
1 |
1 |
1 |
1 |
0.5 |
1.5 |
+2
