ЛЕКЦИЯ 8. Итерационные методы решения СЛАУ.

ЛИТЕРАТУРА. Учебник [1] §6.1. §6.2, §6.3 §6.4.

§ 8.1 Необходимое и достаточное условие сходимости итерационных методов.

В предыдущих лекциях мы рассматривали простейшие итерационные методы решения

СЛАУ. Рассматривали решение задачи в двух постановках.

1) Дана СЛАУ Ax=b. Требуется найти такой вектор , который удовлетворяет неравенству:

. (8.1)

Будем называть это первой постановкой задачи о нахождении приближенного решения.

2) Дана СЛАУ Ax=b. Найти такой вектор , что норма невязки будет меньше нормы невязки нулевого приближения в заданное количество раз.

ОПРЕДЕЛЕНИЕ. Вектором невязки на n-ой итерации называется вектор равный

Пусть - начальное приближение к корню , тогда - первоначальная невязка.

То есть должно быть справедливо соотношение: , где K- заданное целое число.

критерий окончания итераций.

В качестве основного метода будем рассматривать метод простой итерации.

(8.2)

Теорема. Пусть выполнено условие:

(8.3)

Тогда при произвольном начальном приближении метод простой итерации сходится.

Выполним следующее преобразование исходной системы.

Ax=b ↔ ↔

Очевидно, что были проделаны эквивалентные преобразования системы.

ОПРЕДЕЛЕНИЕ. Канонической формой записи явного стационарного метода называется следующая форма записи:

(8.4)

- называется итерационным параметром. Способы выбора параметра рассмотрим ниже.

ОПРЕДЕЛЕНИЕ. Погрешностью решения на n-ой итерации называется вектор

.

Его также называют вектором ошибки на n-ой итерации. Получим уравнение для вектора ошибки.

Для этого возьмем каноническую форму метода (8.4), а также запишем равенство для точного решения:

Вычитая из верхнего равенства нижнее, получим:

Записывая по-другому, с учетом введенного вектора, получим равенство:

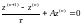(8.5)

Разрешим это равенство относительно . Тогда получим соотношение, связывающее вектор погрешности на n+1-ой итерации и вектор погрешности на n-ой итерации.

Обозначим через S матрицу . Эта матрица называется матрицей перехода от n-ой

итерации к n+1. Можно записать следующее равенство:

Напомним, что называется собственным числом матрицы S , если существует такой ненулевой вектор , что справедливо соотношение: .

Справедлива следующая теорема.

ТЕОРЕМА 8.1. (Необходимое и достаточное условие сходимости итерационных методов). Итерационный метод (8.6) сходится при любом начальном приближении тогда и только тогда, когда все собственные значения матрицы перехода S по модулю меньше 1.

Доказательство. 1. Необходимость. Пусть матрица S имеет собственное число , для которого . Покажем, что найдется такое начальное приближение, что метод разойдется. Пусть - собственный вектор, отвечающий собственному значению .

Возьмем в качестве начального приближения , где - точное решение системы.

Тогда . Очевидно, что ,

Тогда , то есть сходимости нет.

Доказательство. 2. Достаточность. Предположим дополнительно, что матрица S имеет

полный набор собственных векторов . Пусть - собственные числа матрицы S, а - отвечающие им собственные векторы. Разложим вектор по базису:

Тогда . Обозначим спектральный радиус матрицы S так:

. Тогда . Если , то и, следовательно, метод сходится.

Теорема доказана.