ПРЕДМЕТ : Математические методы моделирования физических процессов (МММФП). Лектор Амосова Ольга Алексеевна, доцент кафедры МКМ

Структура дисциплины:

лекция - каждая неделя, 1-ая неделя ПЗ, 2-ая неделя ЛР - 4

РЗ 17 задач, Контрольная работа, Защиты ЛР, Экзамен.

Сайт кафедры: www.mathmod.ru

Разделы: Студенту

Расчетные задания

Лабораторные работы

Файлы с методическими пособиями

Вопросы к экзаменам и зачетам

ЛЕКЦИЯ 1. ВВЕДЕНИЕ В ТЕОРИЮ ПОГРЕШНОСТЕЙ.

Материал к лекции: [1] глава 2, [2] раздел 1.

ЛИТЕРАТУРА

1.Амосов А.А, Дубинский Ю.А., Копченова Н.В. Вычислительные методы. М: Издательский дом МЭИ, 2008.

2.Казенкин К.О. Указания к решению задач по вычислительной математике. Теория погрешностей. Нелинейные уравнения. Системы линейных алгебраических уравнений. М: Издательство МЭИ, 2006.

3 Амосова О.А., Вестфальский А.Е., Крупин Г.В. Упражнения по основам численных методов. М: Издательство МЭИ, 2016.

4. Учебники по МathСad. Дьяконов В. Справочники по МС.

§1.1 Основные типы погрешностей.

Приступая к изложению основ вычислительной математики, следует отметить, что численные методы являются в большинстве случаев приближенными методами, т.е. позволяют получить лишь некоторое приближение к решению исходной задачи. Реализация численных методов сводится к выполнению простейших арифметических операций: сложить, умножить, разделить. При этом следует помнить, что точные результаты посредством выполнения этих операций на ЭВМ также получить нельзя из-за ограниченной разрядности компьютеров. Вопрос о величине погрешностей приобретает в теории погрешностей особое значение.

ИСТОЧНИКИ и КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ.

1. Математическая модель неустранимая погрешность

2. Погрешность исходных данных неустранимая погрешность

3. Метод (алгоритм) решения задачи. методическая погрешность

4. Округления при вычислениях вычислительная погрешность.

ПРИМЕР. Вычисление скорости падающего с высоты h тела.

• Закон сохранения энергии:

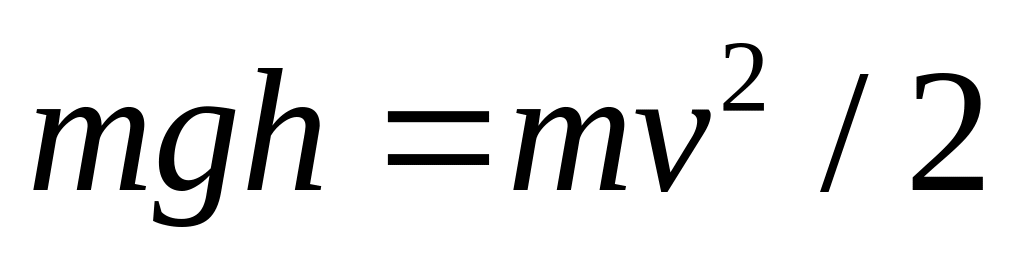
• Отсюда

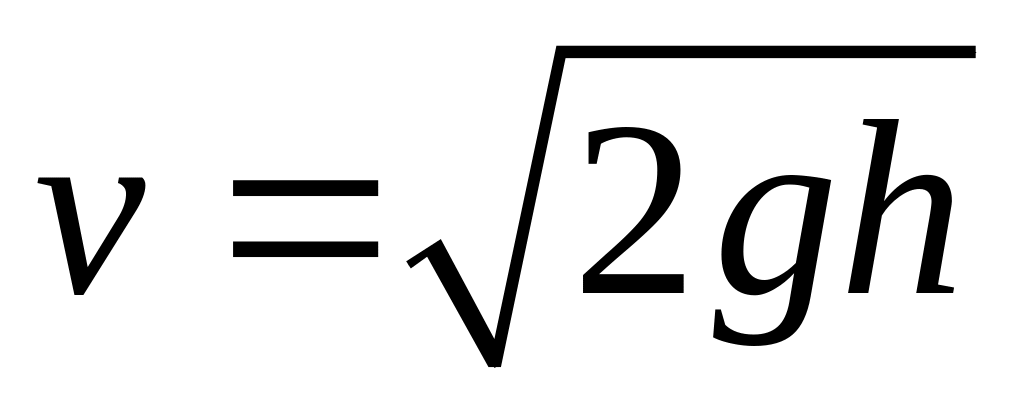
Пусть - точное значение некоторой величины (в общем случае неизвестное), а - приближенное значение той же величины.

Определение. Абсолютной погрешностью числа называется число

(1.1)

Так как - неизвестно, то , как правило, вычислить нельзя. Однако можно получить оценку погрешности: . Величина называется границей абсолютной погрешности. Дальше именно ее будем принимать за величину абсолютной погрешности.

Пример 1. Число = = 1.414213562… .Обычно пользуются таким приближением :

, ,

Точное значение числа неизвестно, т.к. число иррациональное.

Очевидно, что =0.014213….., =0.004213…..

Найдем границу погрешностей для :

Чтобы соотнести погрешность величины и ее значение, вводится понятие относительной погрешности.

Определение. Относительной погрешностью числа называется число

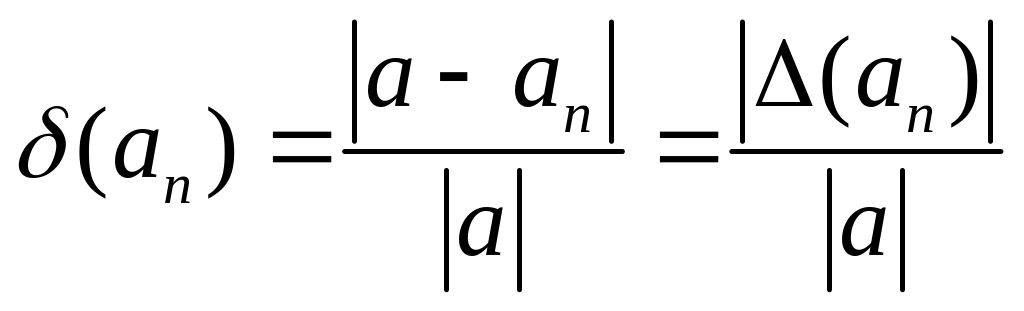(1.2)

Предполагается, что . Так как значения и неизвестны, то для нахождения относительной погрешности используется следующая формула:

(1.3)

Пример 2. Вычислим относительную погрешность числа .

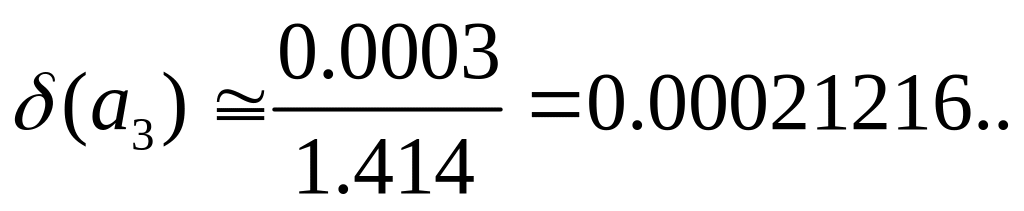Обычно в записи погрешностей удерживают 1-2 ненулевые цифры. Тогда: .

Из формул (1.1) и (1.2) вытекают такие формы записи точных чисел:

,

Пример 3. Согласно ныне действующим (2015 г.) определениям международного Комитета по константам для науки и технологии входящая в закон всемирного тяготения гравитационная постоянная равна:

,

а заряд электрона

Сравнить точность определения этих фундаментальных физических постоянных.

Решение. Найдем относительные погрешности этих констант:

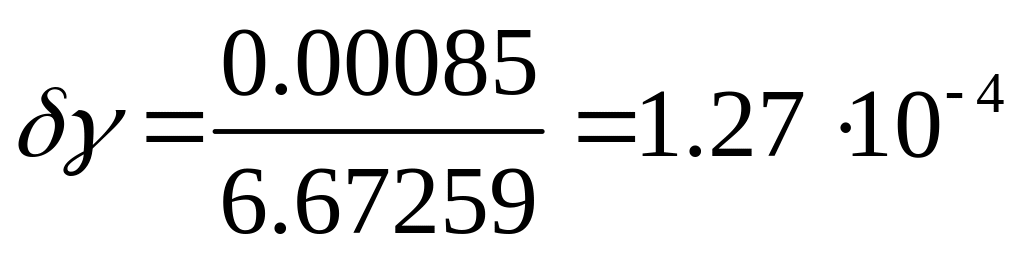
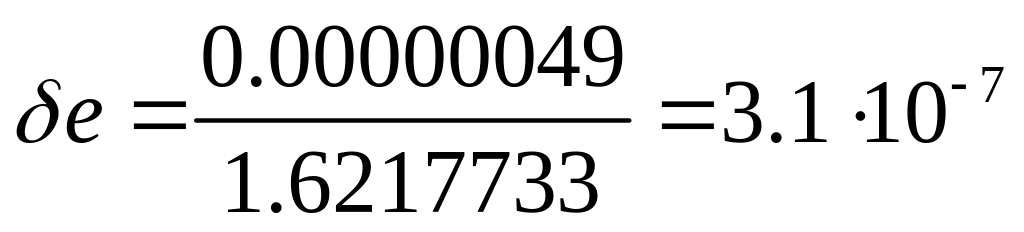
Таким образом, заряд электрона определен существенно точнее.

Понятие точности. Фраза «требуется найти решение с заданной точностью » означает, что ставится задача о нахождении приближенного решения, принятая мера погрешности которого не превышает заданной величины .