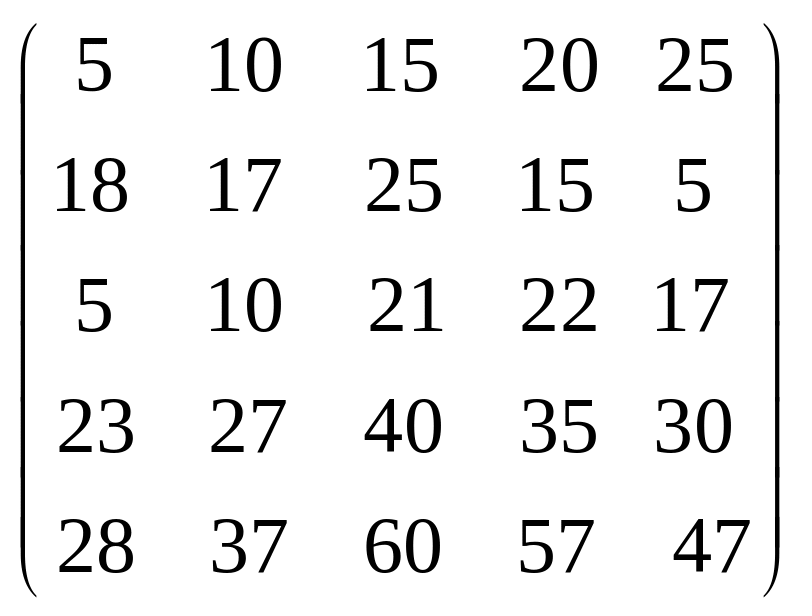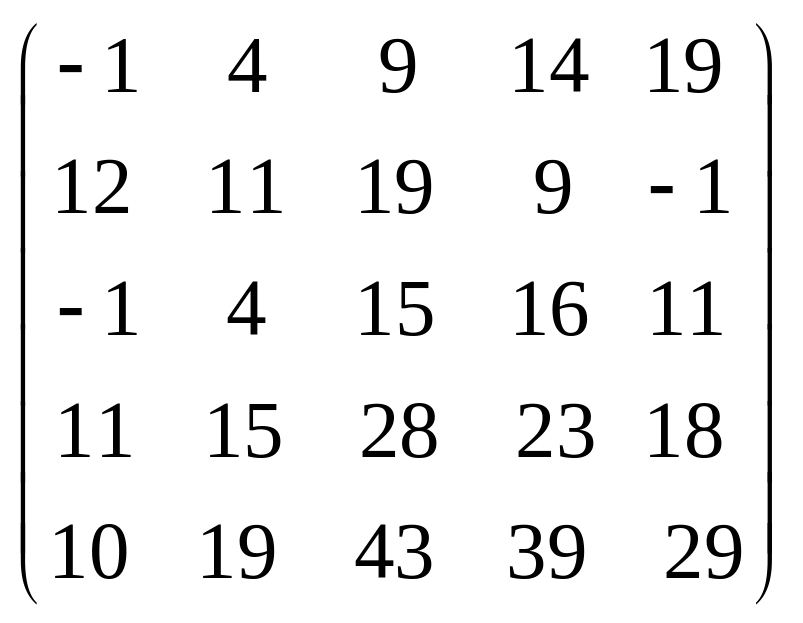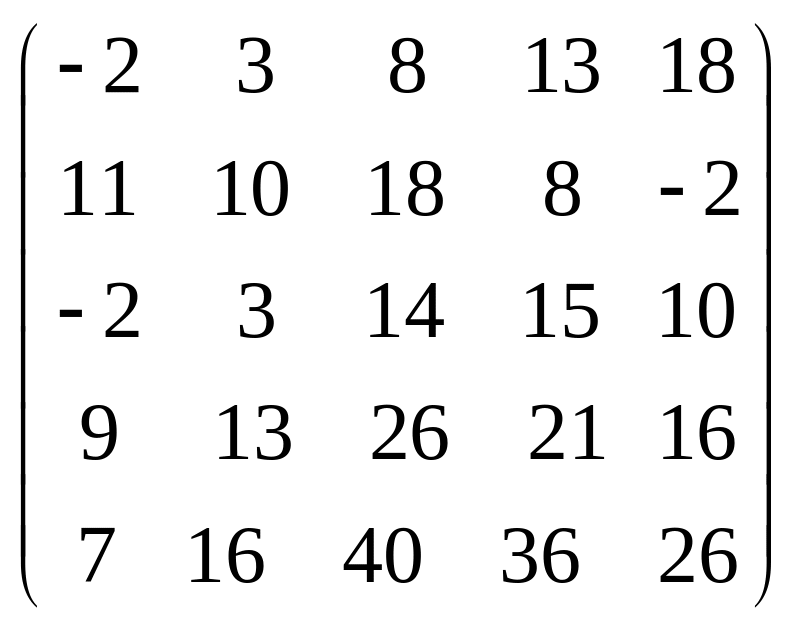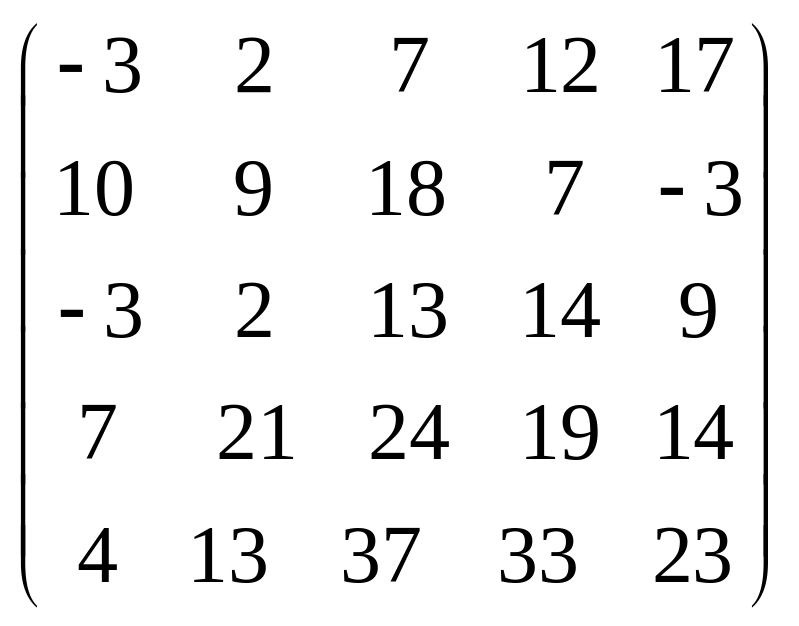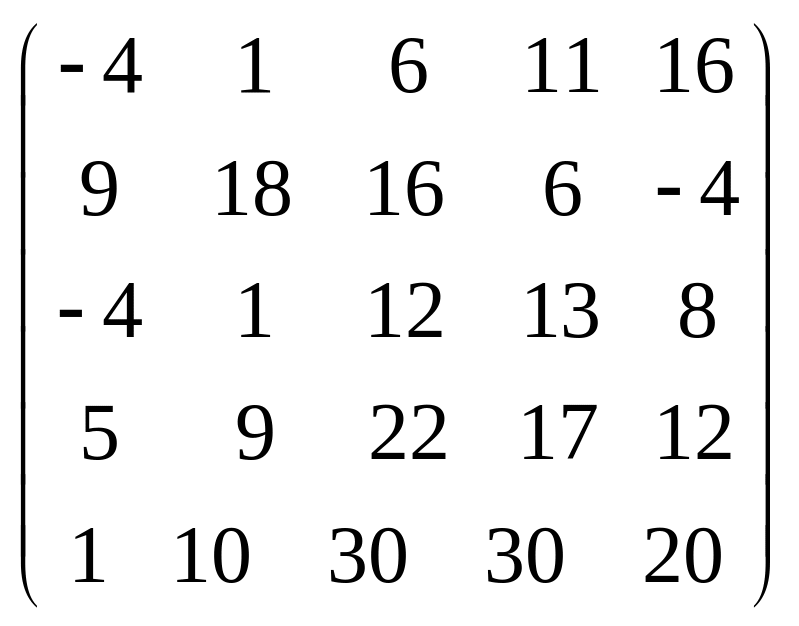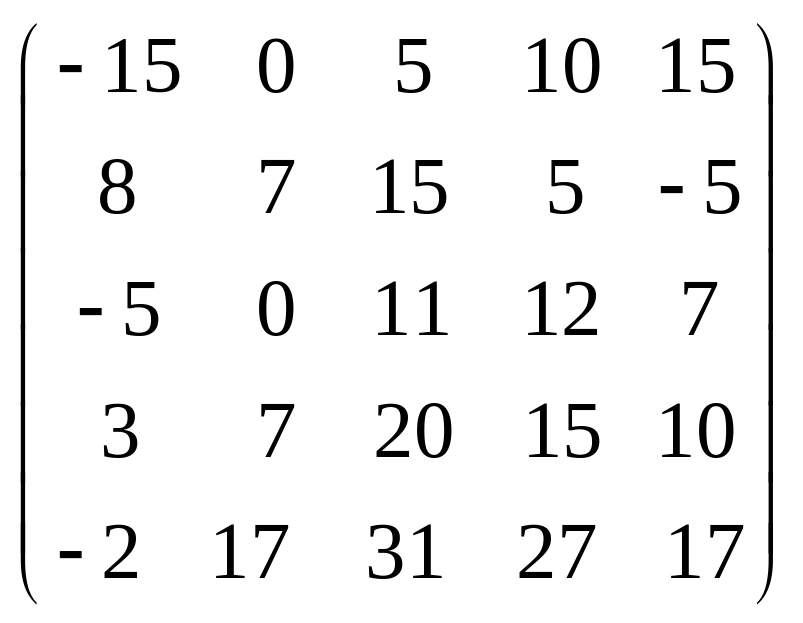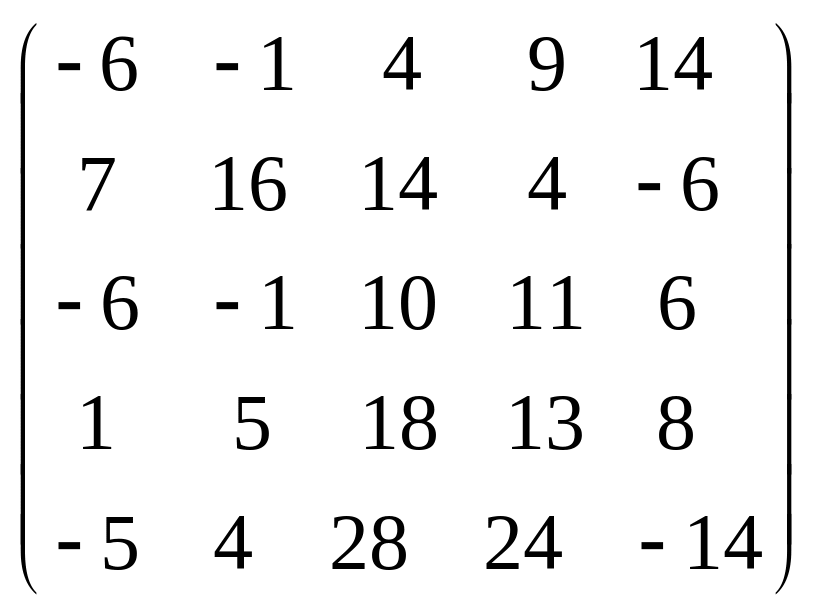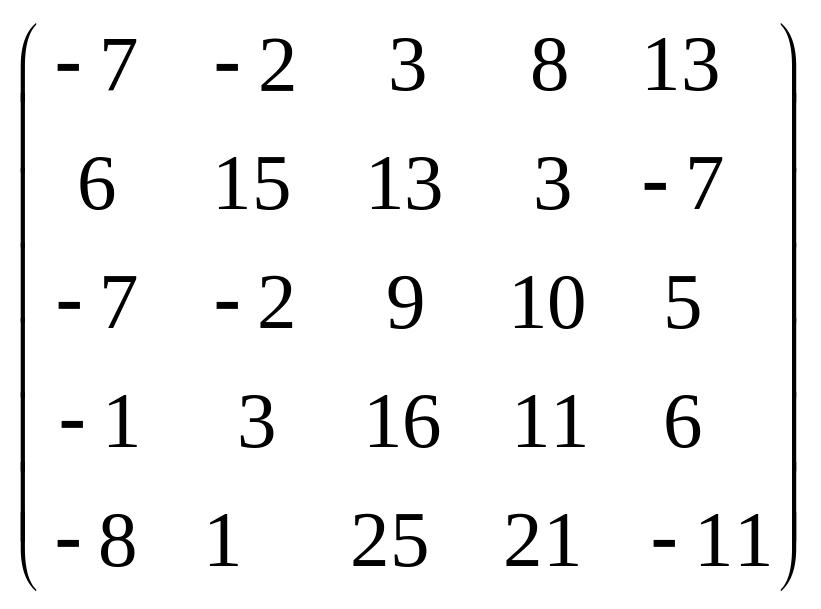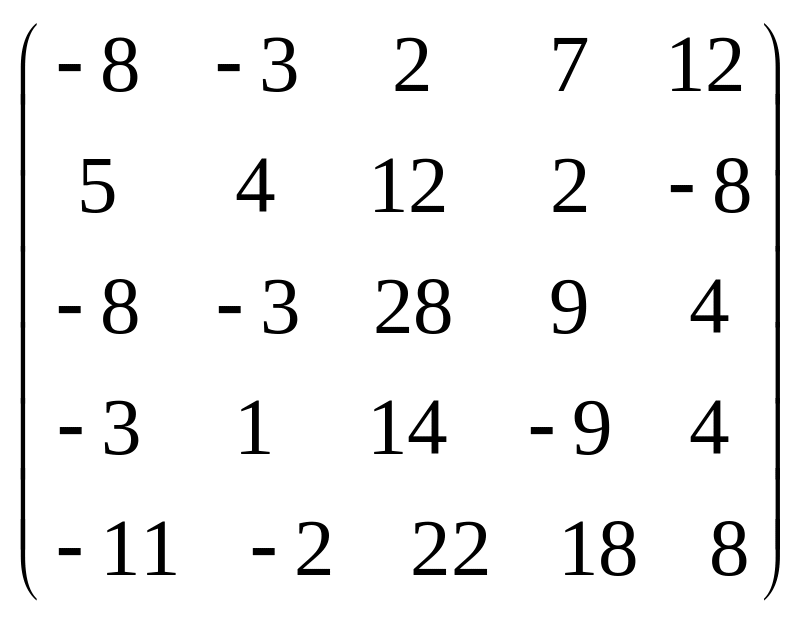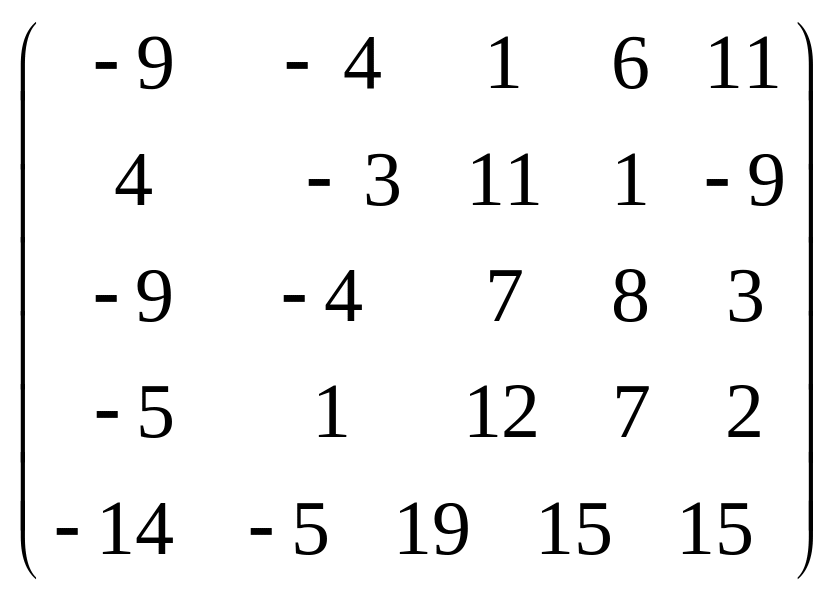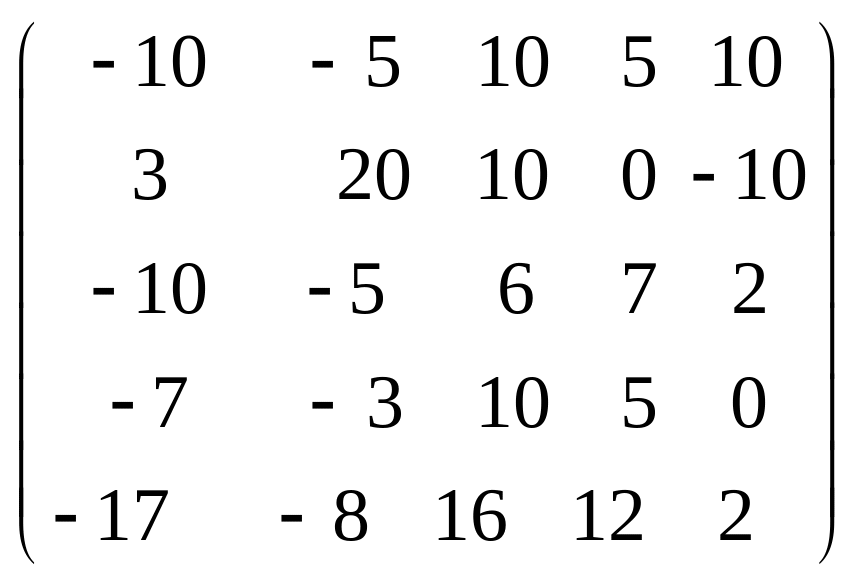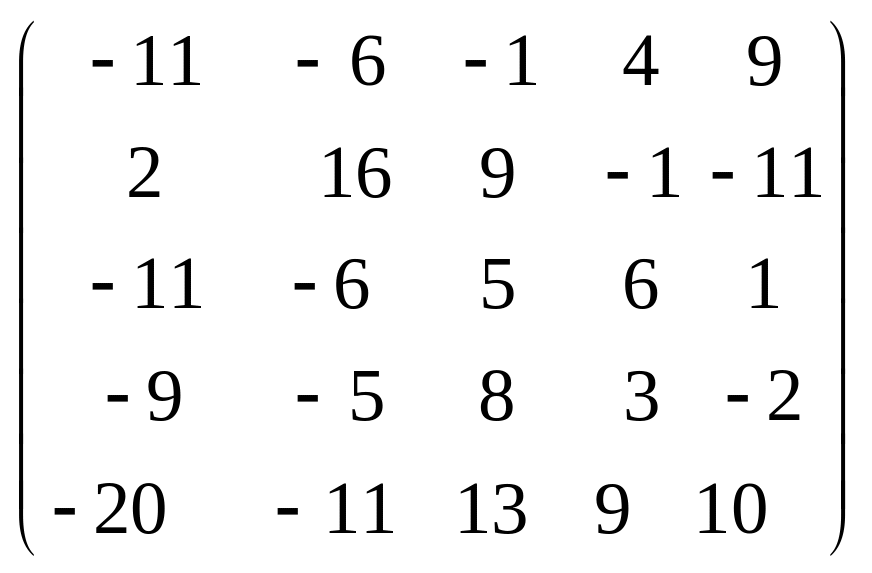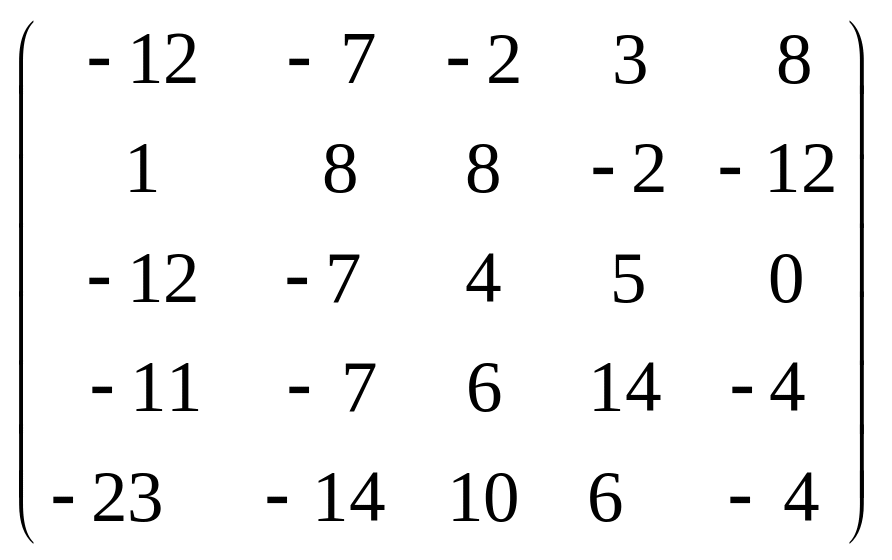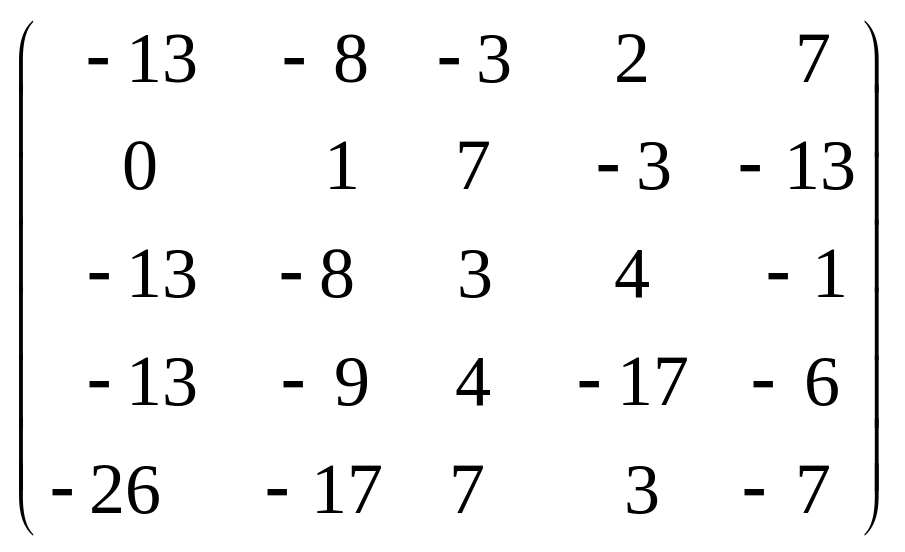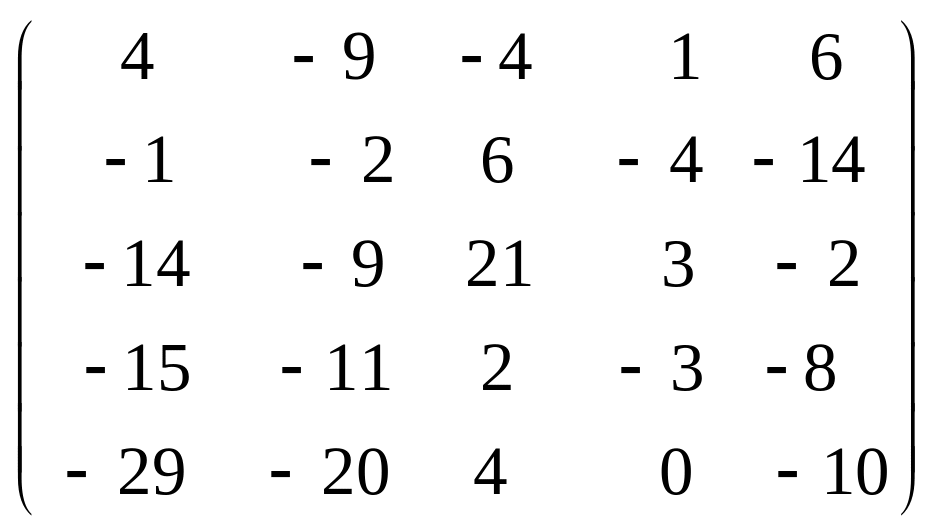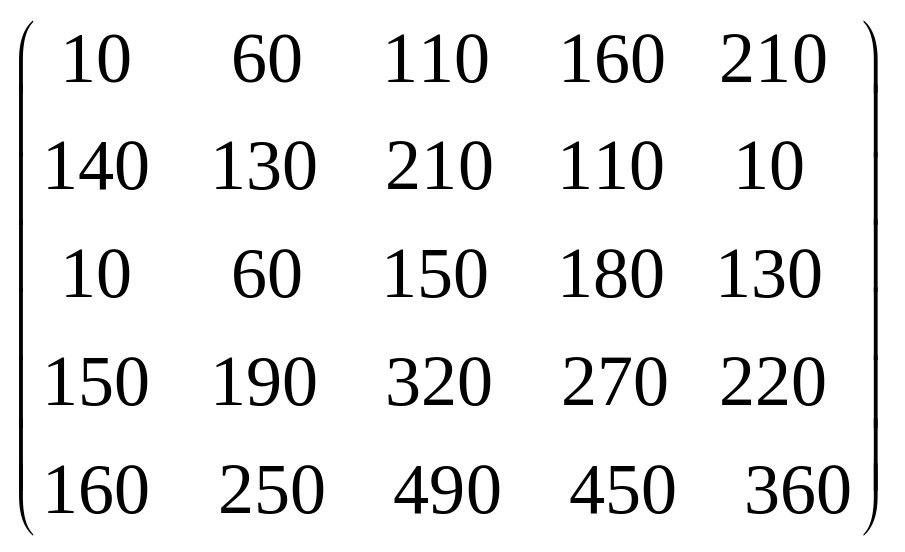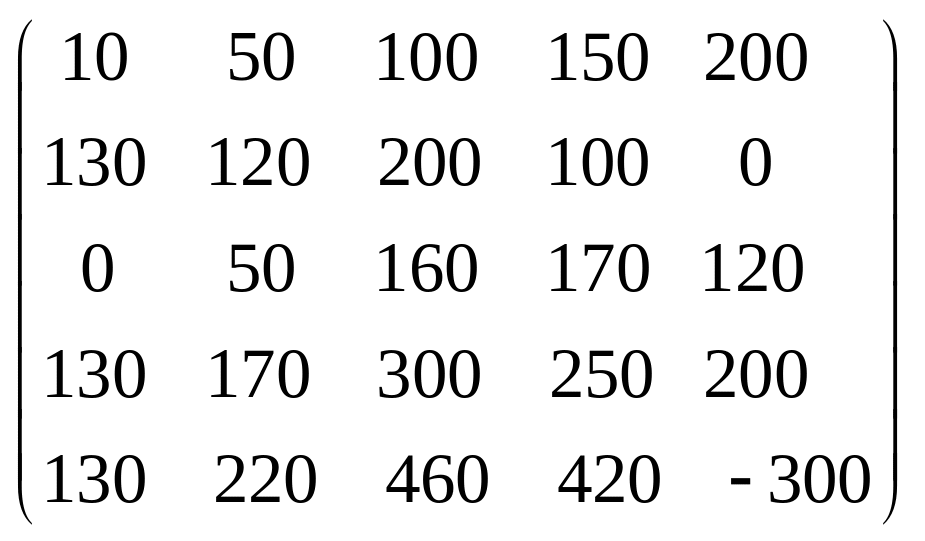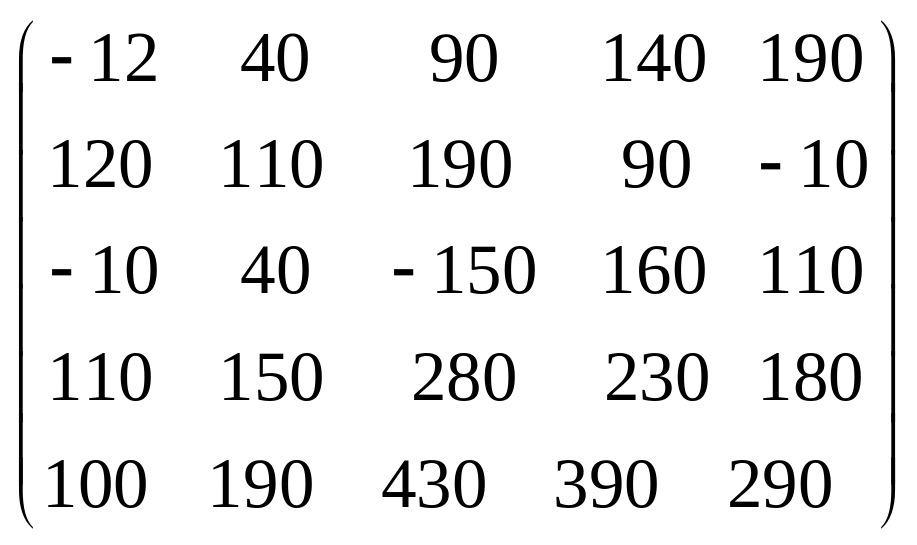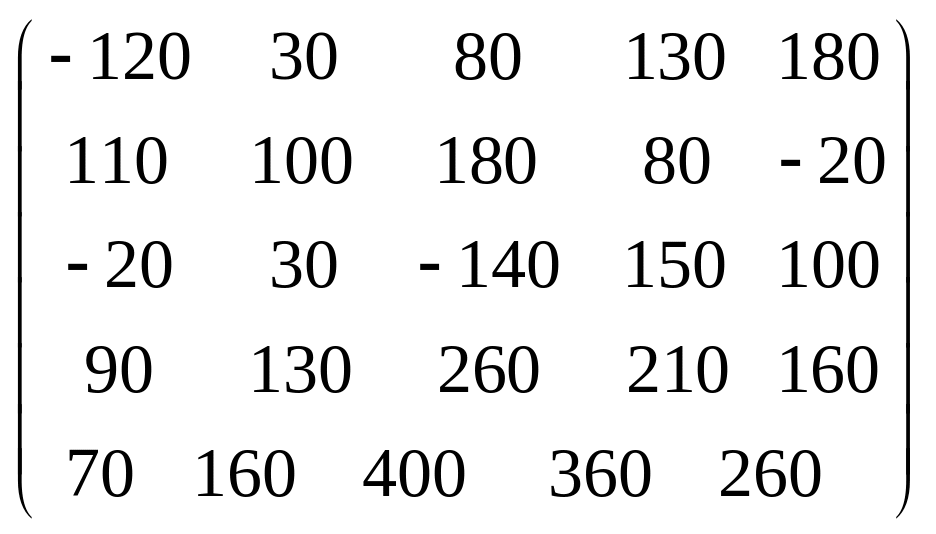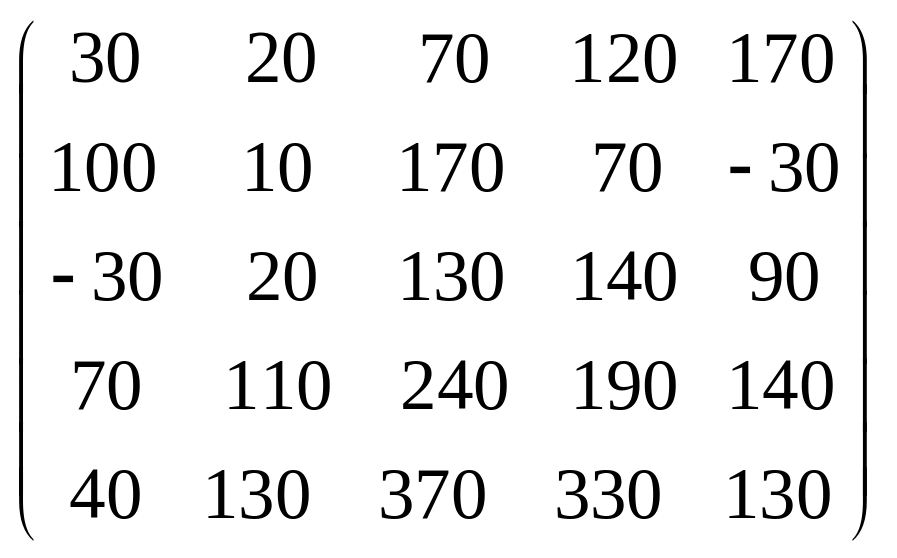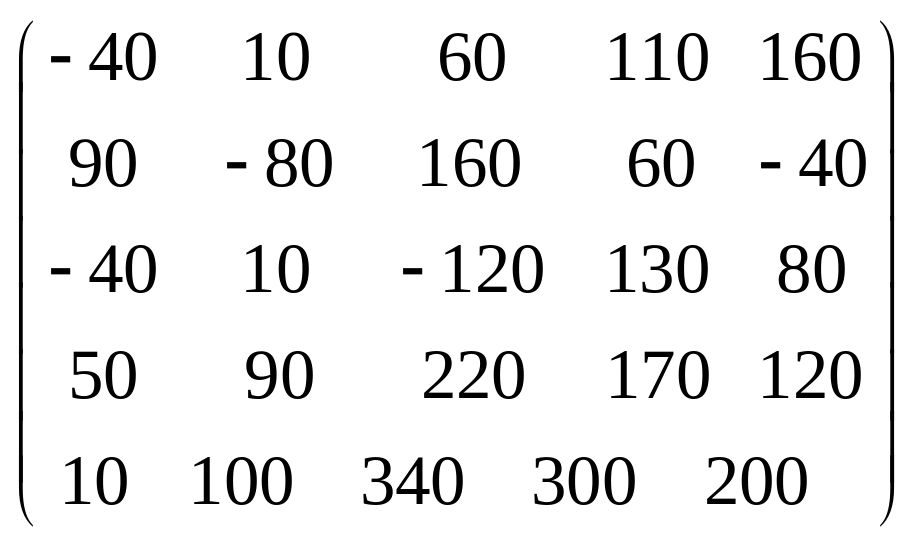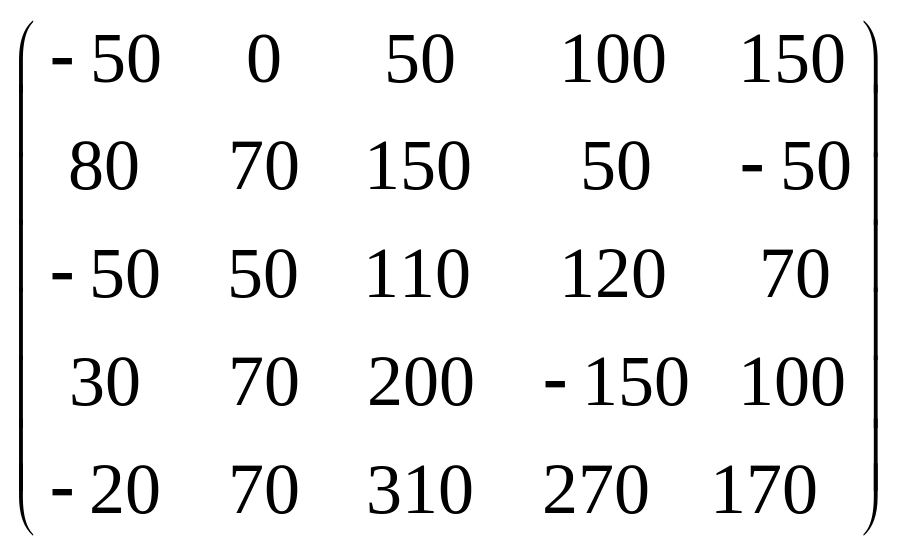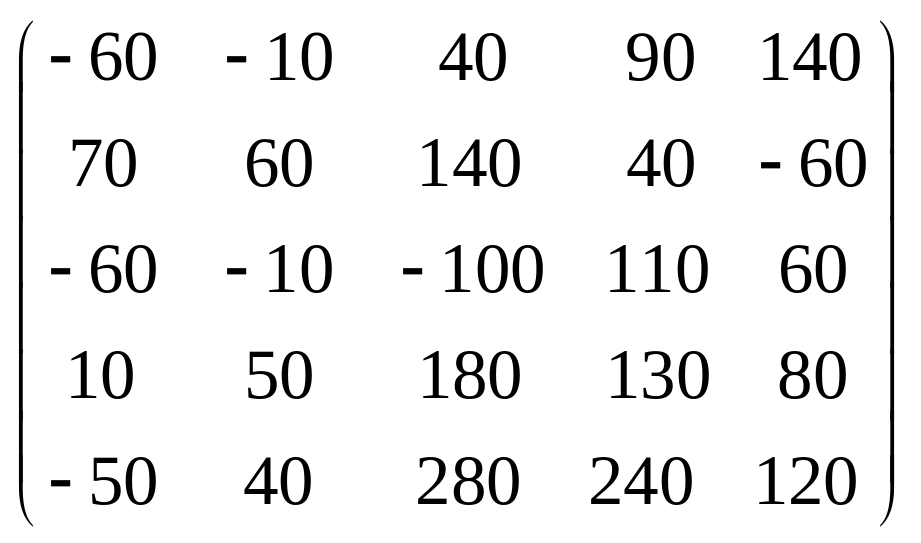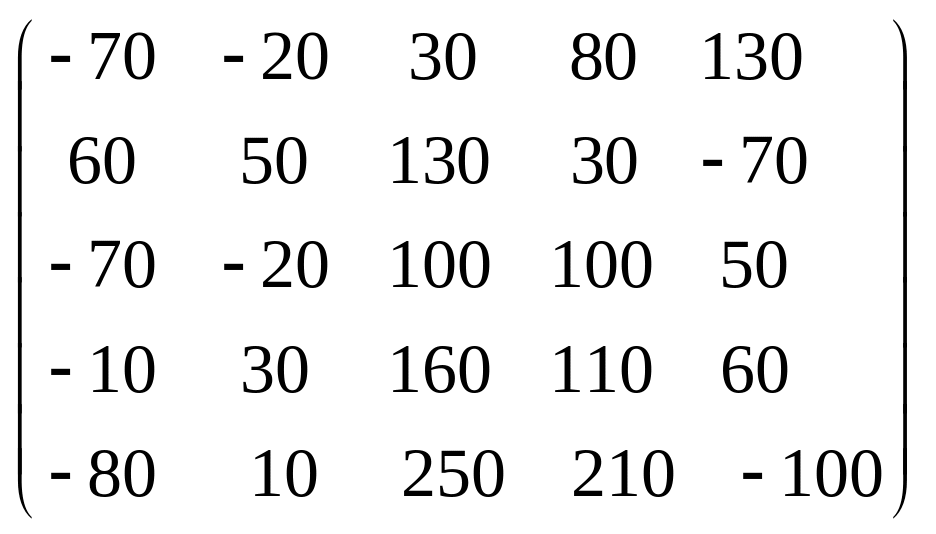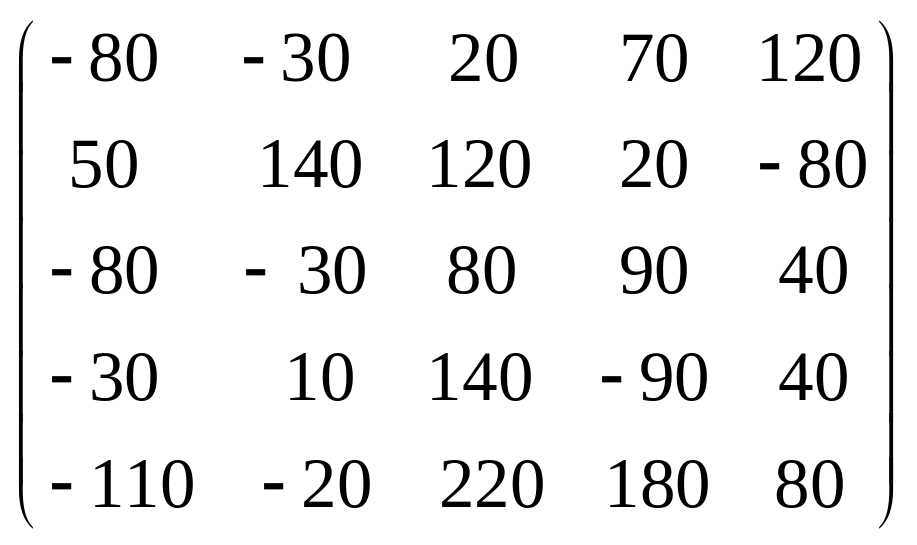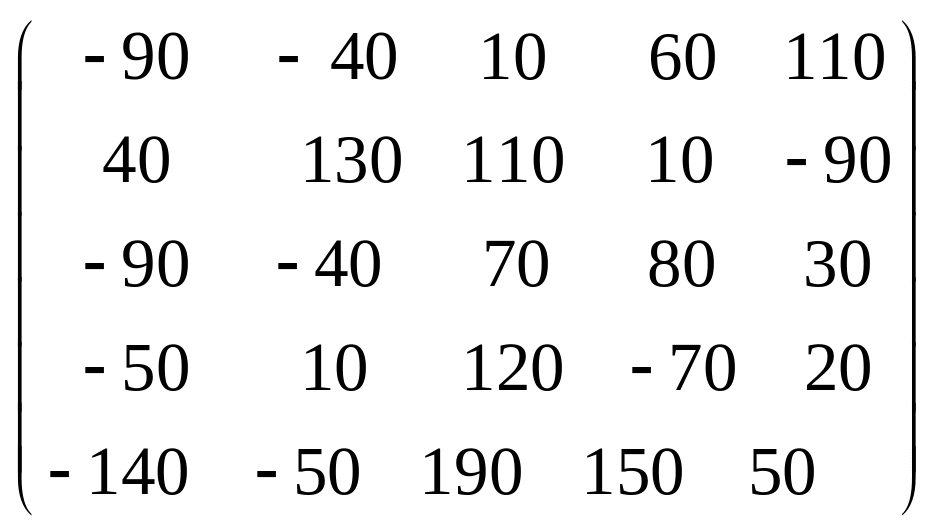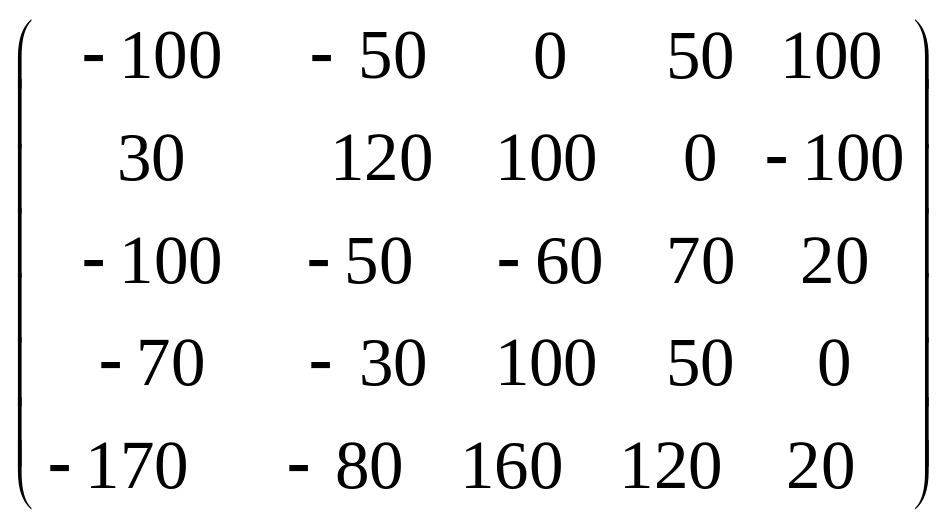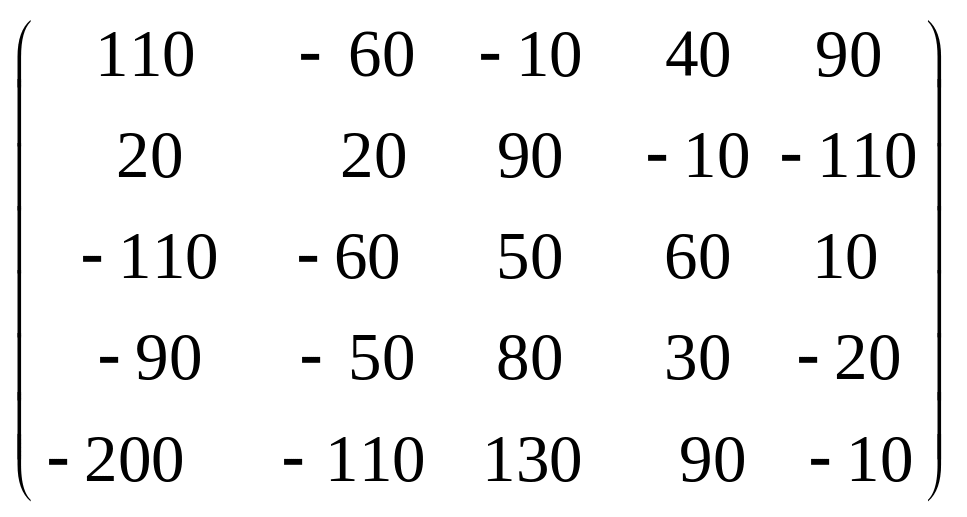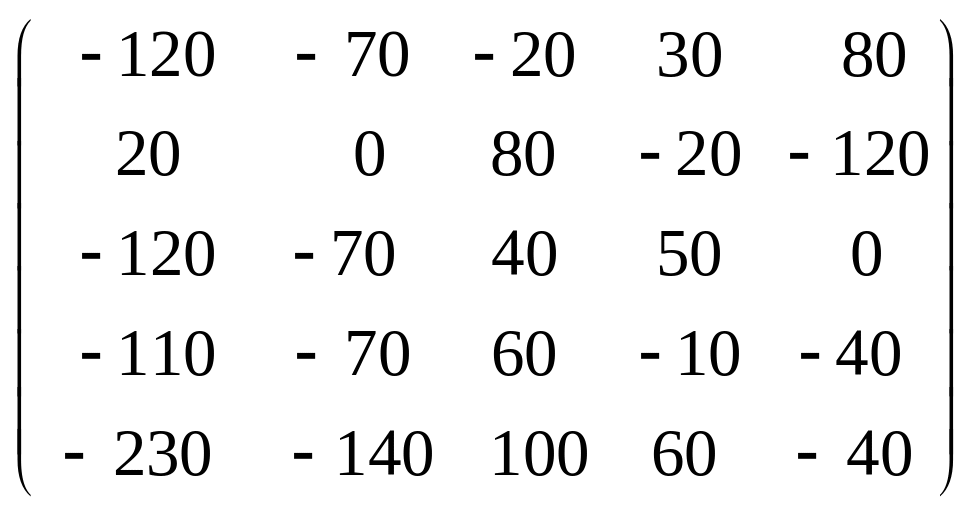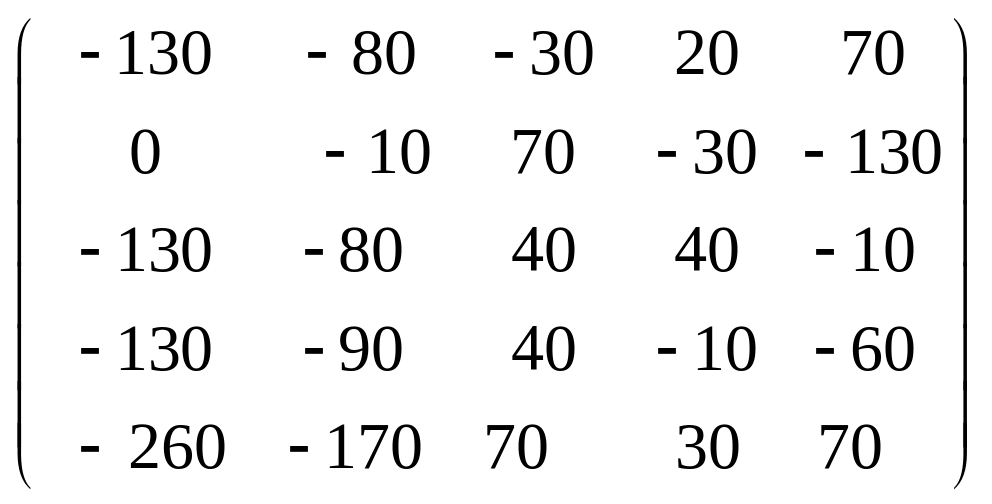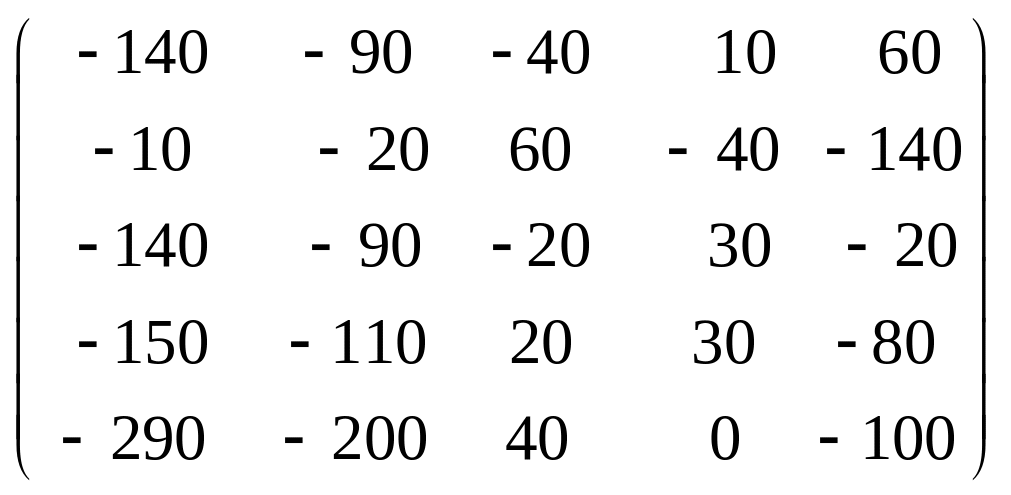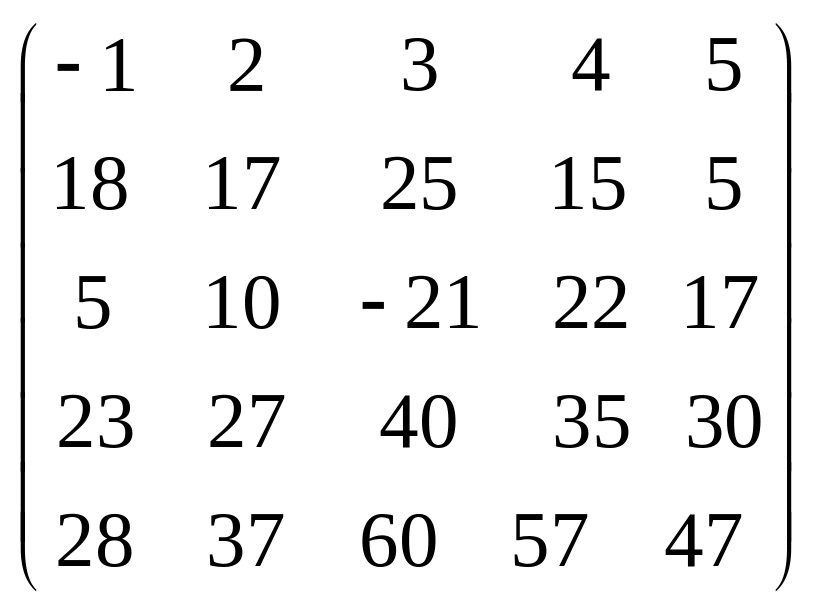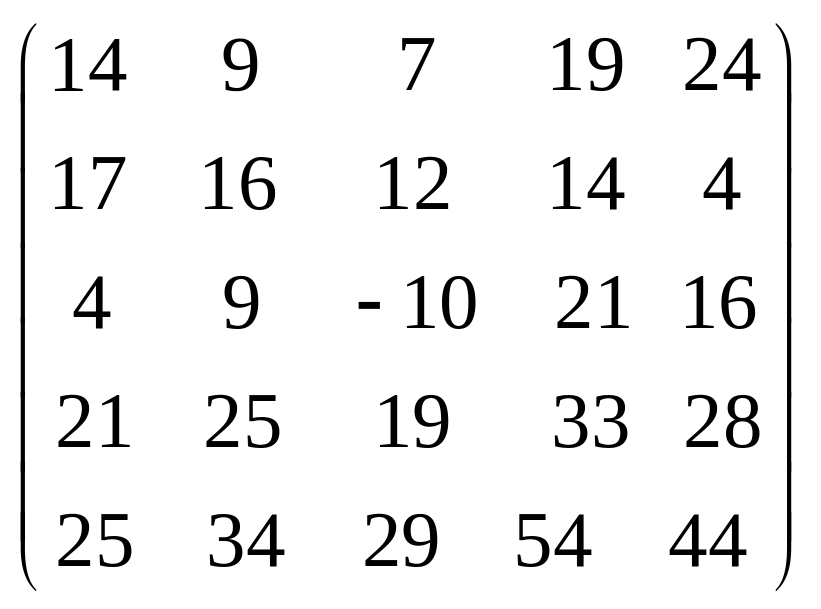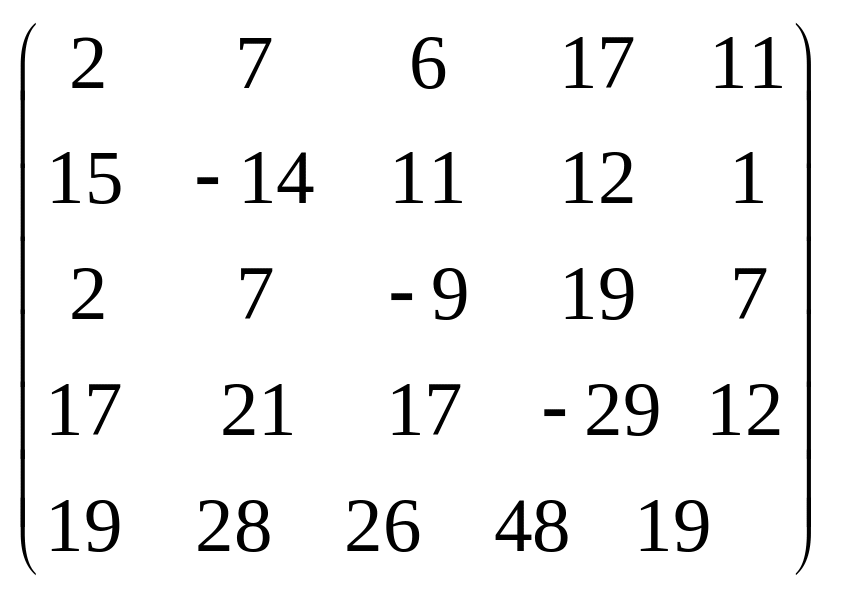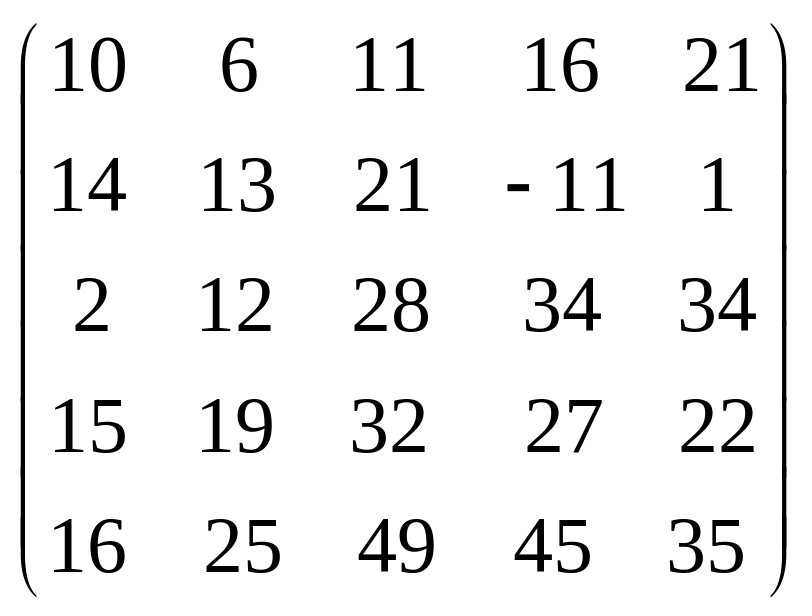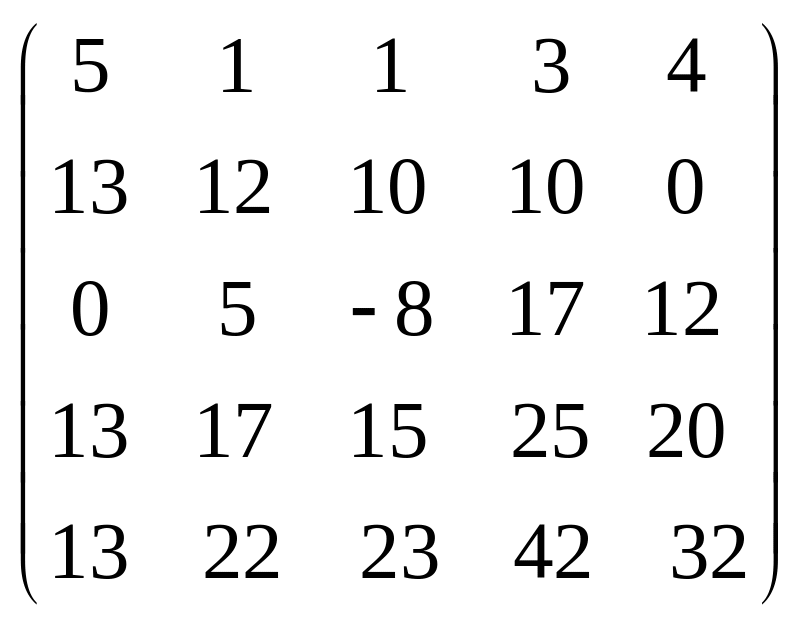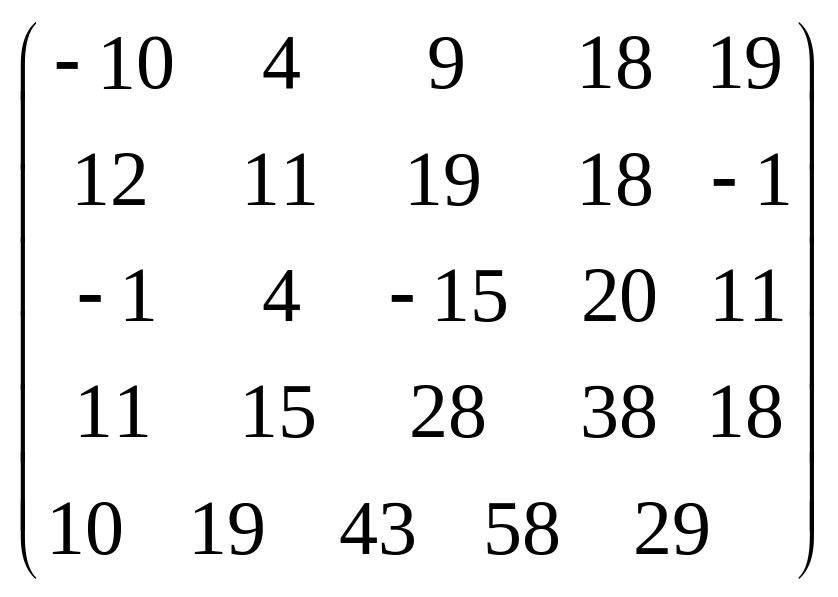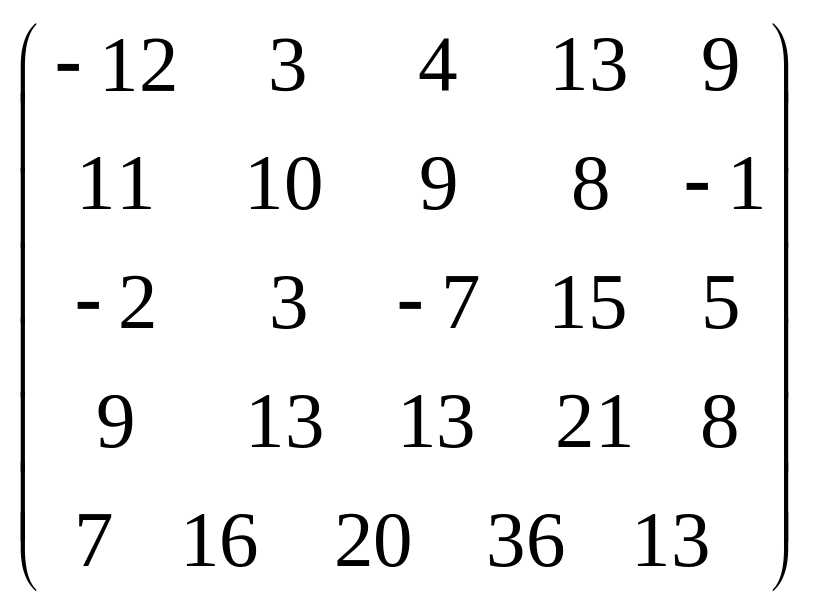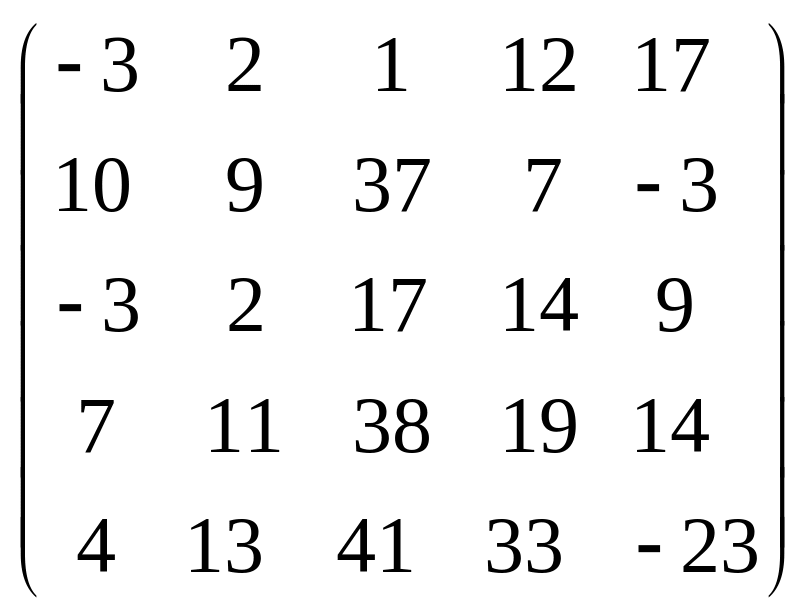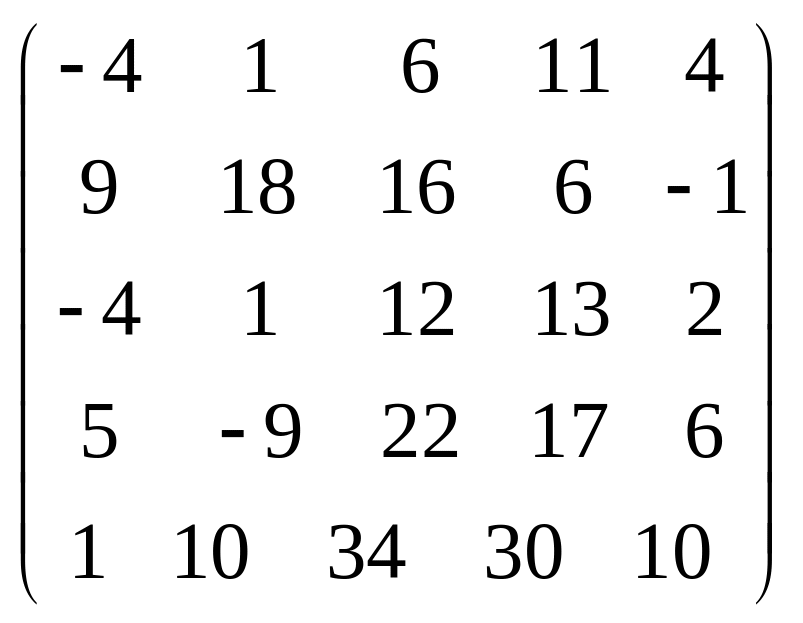ЛАБОРАТОРНАЯ РАБОТА 3
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ ПРЯМЫМИ и ИТЕРАЦИОННЫМИ МЕТОДАМИ. ТЕОРИЯ ВОЗМУЩЕНИЙ
Теоретический материал к данной теме содержится [1, глава 5].
Варианты заданий к задачам 3.1–3.2 даны в ПРИЛОЖЕНИИ 3.A.
ТРЕБОВАНИЯ К ЛАБОРАТОРНОЙ РАБОТЕ 3
1. Задачи 3.1 и 3.2 выполняются с помощью пакета MATHCAD.
Задача 3.1. Дана система уравнений
Исследовать поведение решения системы
в зависимости от
погрешности матрицы A.
ПОРЯДОК РЕШЕНИЯ ЗАДАЧИ:
1. Задать матрицу
.
Вычислить ранг матрицы.
2. Вычислить указанную в варианте норму матрицы A.
3. Вычислить число обусловленности матрицы с помощью встроенной процедуры.
4. Получить возмущенную матрицу A1. Для этого внести погрешность в матрицу A указанным в варианте
способом. Вычислить норму полученной матрицы.
5. Вычислить относительную погрешность
матрицы A1 по формуле
.
6.Составить подпрограмму вычисления нормы вектора, соответствующей норме матрицы.
7. С помощью встроенной процедуры lsolve найти решения систем Ax=b и A1x1=b. Вектор b взять из задачи
3.2 соответствующей размерности.
8. Вычислить относительную погрешность вектора x1 аналогично п.5.
9.Все полученные результаты внести в таблицу.
10. Вычислить практическое число
обусловленности по формуле
.
11. Сравнить теоретический и практический результаты. Оформить отчет по задаче.
Норма
|
|
Норма
|
|
----- |
---------- |
Число обусловленности A= |
|
Число обусловленности A1= |
|
Погрешность матрицы A1=
|
|
Решение системы x |
|
Решение системы x1 |
|
Погрешность Вектора x1=
|
|
=
=
Задача 3.2. Найти решение системы с
точностью
с помощью метода релаксации. Определить
экспериментально параметр релаксации
,
при котором точность
достигается при наименьшем числе
итераций. Построить график зависимости
числа итераций от параметра релаксации.
Произвести расчеты для случая
переменных и для случая
переменных.
УКАЗАНИЕ. Параметр релаксации
следует задавать из условия сходимости
метода:
.
Например: =0.2,
0.4, …, 1.8.
ПРИЛОЖЕНИЕ 3.A.
ВАРИАНТЫ ЗАДАНИЙ К ЛАБОРАТОРНОЙ РАБОТЕ 3
ВНИМАНИЕ! Номер варианта N для лабораторных работ вычисляется по следующей
формуле:
1)
для групп 9–11;
2)
для групп 12–15
(здесь
— номер группы, а
— индивидуальный номер студента по
журналу).
Примечание. Если полученный номер N получился больше значения 50, то принять
N=N-50. Если полученный номер N получился меньше 1, то принять N=N+50.
Таблица к задаче 3.1
|
|
Внесение погрешности |
|
3.1.1 |
|
К элементам 1-го столбца матрицы прибавить 1 |
|
3.1.2 |
|
К элементам 5-ой строки матрицы прибавить 1 |
|
3.1.3 |
|
К элементам 2-го столбца матрицы прибавить 1 |
|
3.1.4 |
|
К элементам 4-ой строки матрицы прибавить 1 |
|
3.1.5 |
|
К элементам 3-го столбца матрицы прибавить 1 |
|
3.1.6 |
|
К элементам 3-ой строки матрицы прибавить 1 |
|
3.1.7 |
|
К элементам 4-го столбца матрицы прибавить 1 |
|
3.1.8 |
|
К элементам 2-ой строки матрицы прибавить 1 |
|
3.1.9 |
|
К элементам 5-го столбца матрицы прибавить 1 |
|
3.1.10 |
|
К элементам 1-ой строки матрицы прибавить 1 |
|
3.1.11 |
|
К элементам 1-го столбца матрицы прибавить 0.5 |
|
3.1.12 |
|
К элементам 5-ой строки матрицы прибавить 0.5 |
|
3.1.13 |
|
К элементам 2-го столбца матрицы прибавить 0.5 |
|
3.1.14 |
|
К элементам 4-ой строки матрицы прибавить 0.5 |
|
3.1.15 |
|
К элементам 3-го столбца матрицы прибавить 0.5 |
|
3.1.16 |
|
К элементам 3-ой строки матрицы прибавить 0.5 |
|
3.1.17 |
|
К элементам 4-го столбца матрицы прибавить 0.5 |
|
3.1.18 |
|
К элементам 2-ой строки матрицы прибавить 0.5 |
|
3.1.19 |
|
К элементам 5-го столбца матрицы прибавить 0.5 |
|
3.1.20 |
|
К элементам 1-ой строки матрица прибавить 0.5 |
|
3.1.21 |
|
К элементам 1-го столбца матрицы прибавить 0.5 |
|
3.1.22 |
|
К элементам 5-ой строки матрицы прибавить 0.5 |
|
3.1.23 |
|
К элементам 2-го столбца матрицы прибавить 0.5 |
|
3.1.24 |
|
К элементам 4-ой строки матрицы прибавить 2 |
|
3.1.25 |
|
К элементам 3-го столбца матрицы прибавить 2 |
|
3.1.26 |
|
К элементам 3-ой строки матрицы прибавить 2 |
|
3.1.27 |
|
К элементам 4-го столбца матрицы прибавить 2 |
|
3.1.28 |
|
К элементам 2-ой строки матрицы прибавить 2 |
|
3.1.29 |
|
К элементам 5-го столбца матрицы прибавить 2 |
|
3.1.30 |
|
К элементам 1-ой строки матрицы прибавить 2 |
|
3.1.31 |
|
К элементам 1-го столбца матрицы прибавить 5 |
|
3.1.32 |
|
К элементам 5-ой строки матрицы прибавить 5 |
|
3.1.33 |
|
К элементам 2-го столбца матрицы прибавить 5 |
|
3.1.34 |
|
К элементам 4-ой строки матрицы прибавить 5 |
|
3.1.35 |
|
К элементам 3-го столбца матрицы прибавить 5 |
|
3.1.36 |
|
К элементам 3-ой строки матрицы прибавить 5 |
|
3.1.37 |
|
К элементам 4-го столбца матрицы прибавить 5 |
|
3.1.38 |
|
К элементам 2-ой строки матрицы прибавить 5 |
|
3.1.39 |
|
К элементам 5-го столбца матрицы прибавить 5 |
|
3.1.40 |
|
К элементам 1-ой строки матрицы прибавить 5 |
|
3.1.41
|
|
К элементам 1-го столбца матрицы прибавить 0.4 |
|
3.1.42 |
|
К элементам 5-ой строки матрицы прибавить 0.4 |
|
3.1.43 |
|
К элементам 2-го столбца матрицы прибавить 0.4 |
|
3.1.44 |
|
К элементам 4-ой строки матрицы прибавить 1 |
|
3.1.45 |
|
К элементам 3-го столбца матрицы прибавить 0.4 |
|
3.1.46 |
|
К элементам 3-ой строки матрицы прибавить 0.4 |
|
3.1.47 |
|
К элементам 4-го столбца матрицы прибавить 0.4 |
|
3.1.48 |
|
К элементам 2-ой строки матрицы прибавить 0.4 |
|
3.1.49 |
|
К элементам 5-го столбца матрицы прибавить 0.4 |
|
3.1.50 |
|
К элементам 1-ой строки матрицы прибавить 0.4 |
|
3.1.51 |
|
К элементам 2-ой строки матрицы прибавить 0.5 |
|
3.1.52 |
|
К элементам 5-го столбца матрицы прибавить 0.5 |
|
Таблица к задаче 3.2
Элементы
матрицы A
задаются формулами: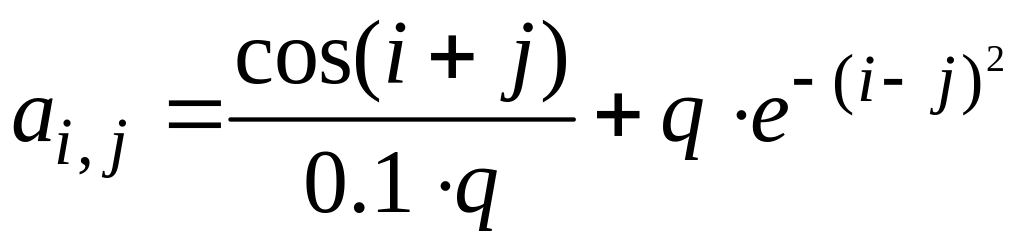 
,
параметр
задается формулой :
,
здесь
– номер варианта, m-
размерность матрицы, указанная в
варианте. Вектор b
задан
в индивидуальном варианте.
N |
|
|
|
N |
|
|
|
3.2.1 |
6
|
|
|
3.2.27 |
5
|
|
|
3.2.2 |
9
|
|
|
3.2.28 |
7
|
|
|
3.2.3 |
7
|
|
|
3.2.29 |
8
|
|
|
3.2.4 |
8
|
|
|
3.2.30 |
6
|
|
|
3.2.5 |
5
|
|
|
3.2.31 |
7
|
|
|
3.2.6 |
7
|
|
|
3.2.32 |
6
|
|
|
3.2.7 |
6
|
|
|
3.2.33 |
8
|
|
|
3.2.8 |
10
|
|
|
3.2.34 |
6
|
|
|
3.2.9 |
5
|
|
|
3.2.35 |
9
|
|
|
3.2.10 |
9 |
|
|
3.2.36 |
6 |
|
|
3.2.11 |
8
|
|
|
3.2.37 |
5 |
|
|
3.2.12 |
9
|
|
|
3.2.38 |
9
|
|
|
3.2.13 |
7 |
|
|
3.2.39 |
8 |
|
|
3.2.14 |
4
|
|
|
3.2.40 |
8
|
|
|
3.2.15 |
6
|
|
|
3.2.41 |
6
|
|
|
3.2.16 |
8
|
|
|
3.2.42 |
8
|
|
|
3.2.17 |
9
|
|
|
3.2.43 |
6
|
|
|
3.2.18 |
7
|
|
|
3.2.44 |
7
|
|
|
3.2.19 |
6
|
|
|
3.2.45 |
6
|
|
|
3.2.20 |
10
|
|
|
3.2.46 |
8
|
|
|
3.2.21 |
8
|
|
|
3.2.47 |
9
|
|
|
3.2.22 |
5
|
|
|
3.2.48 |
7
|
|
|
3.2.23 |
9
|
|
|
3.2.49 |
10
|
|
|
3.2.24 |
6
|
|
|
3.2.50 |
8
|
|
|
3.2.25 |
7
|
|
|
3.2.51 |
9
|
|
|
3.2.26 |
4
|
|
|
3.2.52 |
6
|
|
|
+
