Гистограмма выборки debug:

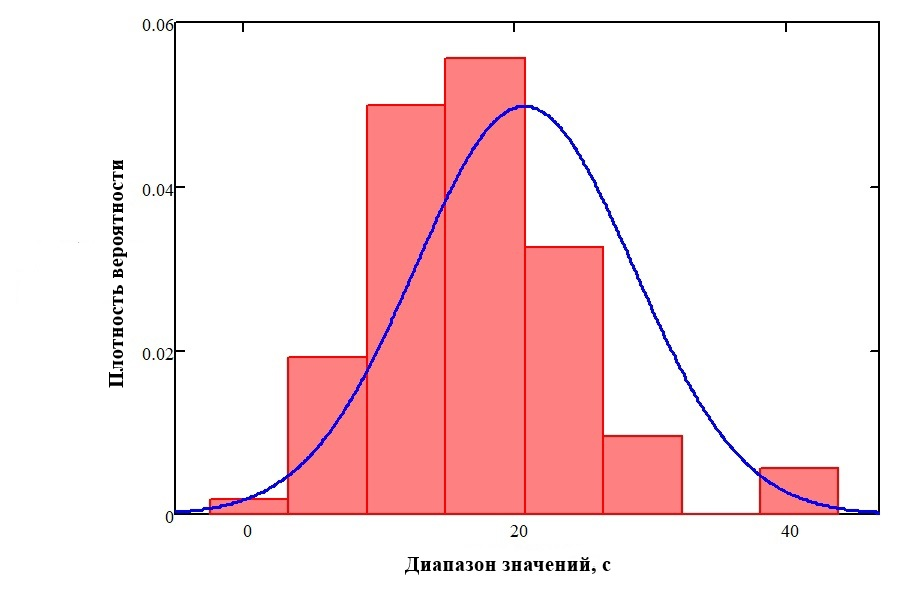
Рис. 1. Гистограмма распределения плотности вероятности выборки debug

Таблица 7 – значения интервалов и частот попадания выборки realise – одинарная точность

Граница интервала	Кол-во элементов, попавших в интервал
[13,3265;17,5955]	10
[17,5956;21,8645]	20
[21,8645;26,1335]	34

Продолжение таблицы 7

[26,1335;30,4025]	14
[30,4025;34,6715]	8
[34,6715;38,9405]	0
[38,9405;43,2095]	0
[43,2095;47,4785]	1

Гистограмма выборки realise – одинарная точность:

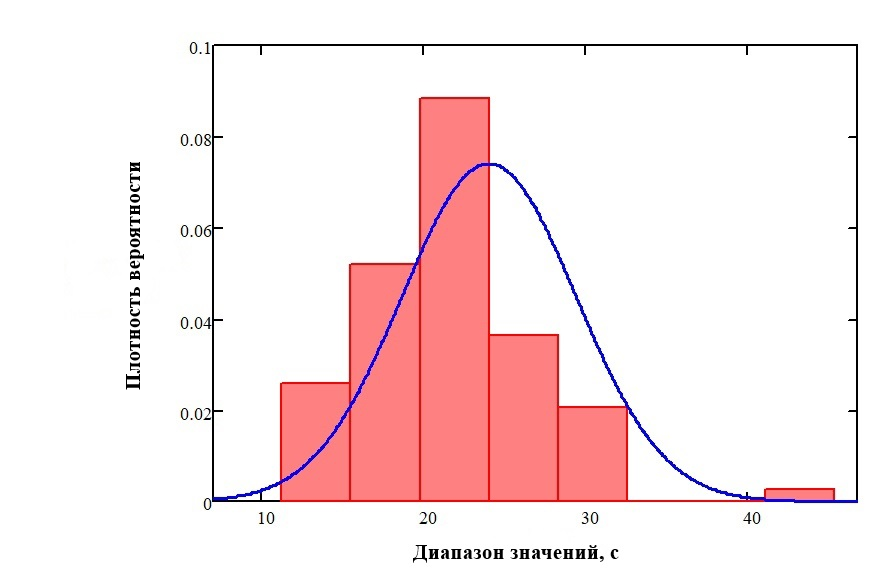
Рис. 2. Гистограмма распределения плотности вероятности выборки realise – одинарная точность.

Таблица 8 – значения интервалов и частот попадания выборки realise – двойная точность

Граница интервала	Кол-во элементов, попавших в интервал
[27,3005;33,0815]	2
[33,0815;38,8625]	5
[38,8625;44,6435]	10
[44,6435;50,4245]	15
[50,4245;56,2055]	29
[56,2055;61,9865]	20
[61,9865;67,7675]	9
[67,7675;73,5485]	5

Гистограмма выборки realise – двойная точность:

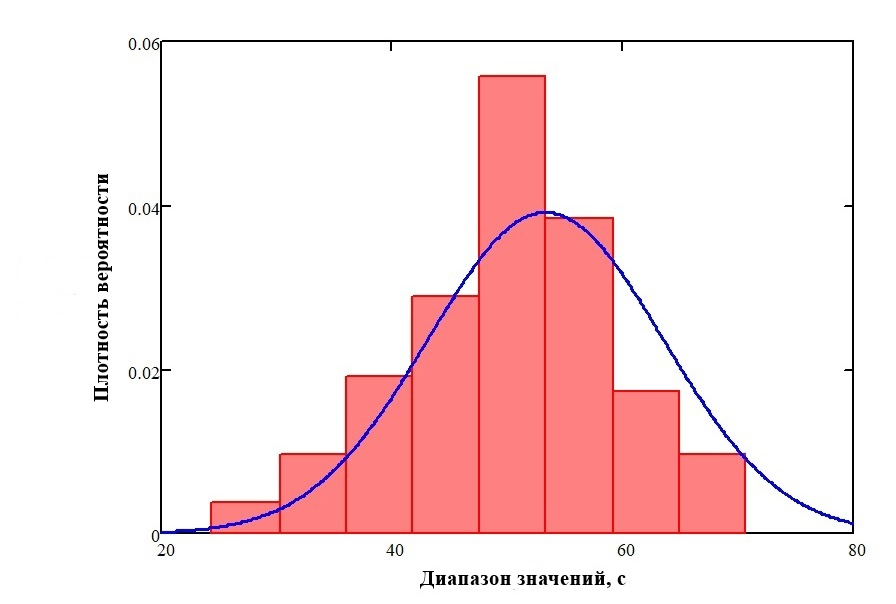
Рис. 3. Гистограмма распределения плотности вероятности выборки realise – двойная точность.

Исследование производительности при параллельных расчетах.

Таблица 9 – результаты исследования производительности при параллельных расчетах

Количество одновременно запущенных программ	Время выполнения каждой программы, с
2	Т1 = 18.96
	Т2 = 19.43
3	Т1 = 24.78
	Т2 = 26.14
	Т3 = 26.74
4	Т1 = 35.65
	Т2 = 35.12
	Т3 = 35.65
	Т4 = 34.60
5	Т1 = 33.15
	Т2 = 38.87
	Т3 = 36.75
	Т4 = 36.09
	Т5 = 36.32

Продолжение таблицы 9

6	Т1 = 51.24
	Т2 = 45.25
	Т3 = 53.05
	Т4 = 52.64
	Т5 = 53.70
	Т6 = 52.14
7	Т1 = 68.43
	Т2 = 63.71
	Т3 = 67.42
	Т4 = 58.65
	Т5 = 68.21
	Т6 = 62.30
	Т7 = 69.85
8	Т1 = 73.15
	Т2 = 71.15
	Т3 = 65.32
	Т4 = 73.14
	Т5 = 65.14
	Т6 = 69.00
	Т7 = 70.81
	Т8 = 71.51

Построим графическую зависимость времени выполнения программ в зависимости от их количества.

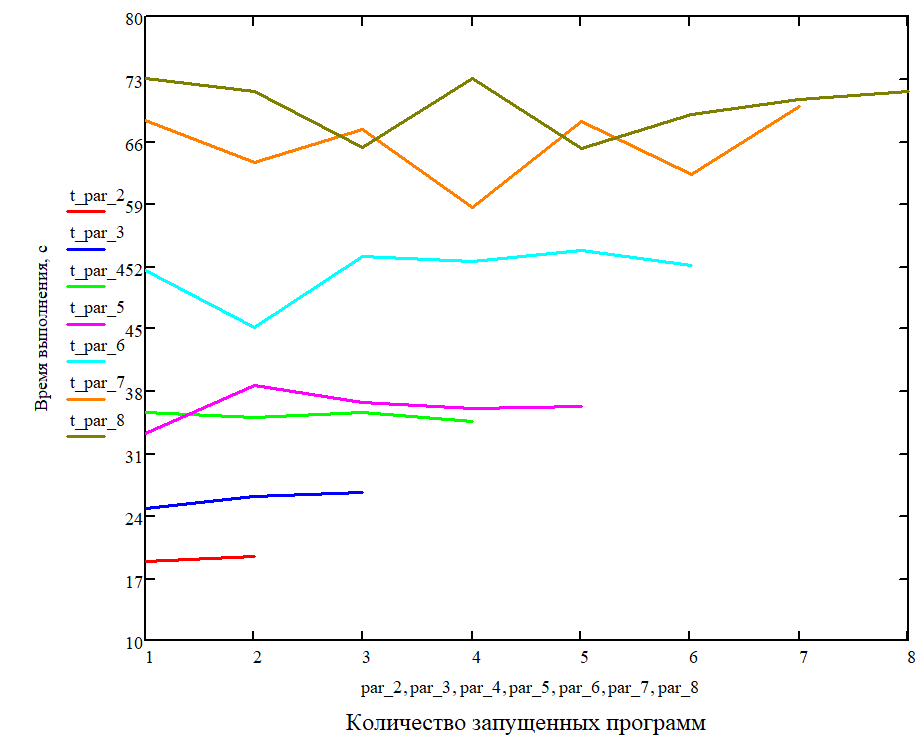
Рис. 4. Зависимость времени выполнения от количества запущенных программ

Выделим для каждого измерения максимальное время выполнения и построим зависимость максимального времени выполнения от числа запущенных программ.

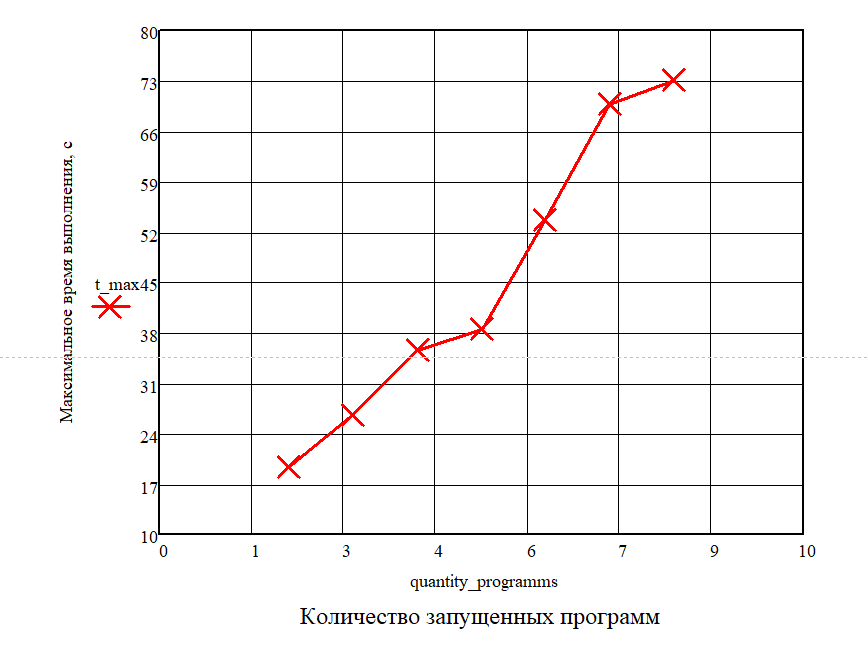
Рис. 5. Зависимость максимального времени выполнения от числа запущенных программ

Вывод.

• В соответствие с заданием была создана программа для исследования производительности ПК на языке высокого уровня FORTRAN с применением математической библиотеки IMSL.

• Зависимость времени выполнения расчетов на одном и том же компьютере одной версии программы происходит по нормальному закону распределения.

• Время выполнения программы в режиме debug несильно отличается от режима realise. Это связано с тем что в режиме realise по умолчанию используется оптимизация, а также с тем что смена режима влияет лишь на подготовительную часть программы, которую написали мы.