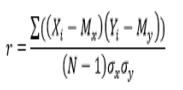Определим основные характеристики всех выборок.
Таблица 5 – основные характеристики выборок
Характеристика |
Расчетная формула |
debug |
realise, одинарная точность |
realise, двойная точность |
Объем выборки |
N |
90 |
||
Размах выборки |
R = Tmax - Tmin |
46,356 |
34,15 |
46,25 |
Середина размаха |
Rсер = Tmin + (Tmax - Tmin) / 2 |
29,162 |
30,865 |
52,195 |
Медиана |
Ме = (TN/2 + TN/2 + 1) / 2 |
20,315 |
24,215 |
54,44 |
Мат. ожидание |
M = ∑T / N |
20,653 |
23,999 |
53,315 |
Мода |
Наиболее встречающийся элемент |
21,5 |
22,28 |
53,76 |
Верхний предел количества интервалов |
5 ∙ lg(N) |
9,771 |
||
Нижний предел количества интервалов |
1 + 3,322 ∙ lg(N) |
7,492 |
||
Окончательное количество интервалов |
7,492 < m < 9,771 |
8 |
||
Ширина интервала |
S = R / m |
5,795 |
4,269 |
5,781 |
Дисперсия |
D = (∑(Ti - М)2) /(N - 1) |
64.185 |
28,973 |
103,738 |
Среднеквадратичное отклонение |
σ = √D |
8,012 |
5,383 |
10,185 |
Ассиметрия |
А = ∑(Ti - М)3 / (σ3 ∙ (N - 1)) |
1,056 |
0,946 |
-0,189 |
Продолжение таблицы 5
Эксцесс |
Е = ∑[(Ti - М)4 / (σ4 ∙(N - 1))] - 3 |
2,521 |
3 |
-0,437 |
Коэффициент корреляции |
|
0,983 |
0,958 |
0,952 |
Анализируя результаты, мы видим что для:
Результатов в режиме debug размах выборки и середина размаха превышают мат. ожидание, а вот медиана выборки близка к мат. ожиданию. Ассиметрия и эксцесс выборки больше единицы. Отсюда можем сделать вывод, что получившаяся выборка далека от нормального распределения, основная часть элементов выборки незначительно превышает мат. ожидание и сконцентрированы возле него.
Результатов в режиме realise с одинарной точностью размах выборки и середина размаха превышают мат. ожидание, а вот медиана выборки близка к мат. ожиданию. Ассиметрия меньше, а эксцесс выборки больше единицы. Отсюда можем сделать вывод, что получившаяся выборка далека от нормального распределения, основная часть элементов выборки незначительно ниже мат. ожидание и сконцентрированы возле него.
Результатов в режиме realise с двойной точностью размах выборки ниже мат. ожидание, а вот медиана выборки и середина размаха близки к мат. ожиданию. Ассиметрия и эксцесс выборки меньше единицы. Отсюда можем сделать вывод, что получившаяся выборка также далека от нормального распределения, но именно она характерна для нормального распределения. Основная часть элементов выборки незначительно ниже мат. ожидание и распределены по всей области выборки
Коэффициент корреляции во всех трех расчетах попадает в диапазон сильной прямой корреляции, следовательно, полученные данные сильно зависимы друг от друга.
Для наглядного исследования результатов построим гистограммы плотности вероятности каждой из выборок, поверх которых нанесем график нормального распределения.
Таблица 6 – значения интервалов и частот попадания выборки debug
Граница интервала |
Кол-во элементов, попавших в интервал |
[0,3705;6,1655] |
1 |
[6,1655;11,9605] |
10 |
[11,9605;17,7555] |
26 |
[17,7555;23,5505] |
29 |
[23,5505;29,3455] |
17 |
[29,3455;35,1405] |
5 |
[35,1405;40,9355] |
0 |
[40,9355;46,7305] |
3 |