Национальный Исследовательский Университет

«МЭИ»

кафедра «АЭС»

Отчет по типовому расчету по курсу

«Информационные и сетевые технологии ядерной энергетики»

Группа: ТФ-12-20

Студент: Долгов Р.Н.

Преподаватель: Воробьев Ю.Б.

Дата выполнения отчета: 04.03.24

Москва 2024

Содержание

1. Цель работы................................................................................................................3

2. Сведения о содержании библиотеки IMSL.............................................................3

3. Математическое содержание используемых процедур.........................................4

4. Содержание используемых функций.......................................................................4

4.1. Процедура LFSHF.................................................................................................

4.1.1. Алгоритм............................................................................................................

4.1.2. Программирование............................................................................................

4.1.3. Результаты..........................................................................................................

4.2. Процедура LFIHF..................................................................................................

4.2.1. Алгоритм............................................................................................................

4.2.2. Программирование............................................................................................

4.2.3. Результаты..........................................................................................................

4.3. Процедура LFDHF................................................................................................

4.3.1. Алгоритм............................................................................................................

4.3.2. Программирование............................................................................................

4.3.3. Результаты..........................................................................................................

5. Вывод............................................................................................................................

6. Список литературы......................................................................................................

Цель работы

Развитие у студентов навыков использования современных информационных технологий применительно к задачам ядерной энергетики.

Если рассматривать задачи связанные с научно-исследовательской и конструкторской деятельностью в данной области, то основная их специфика в настоящее время характеризуется следующим:

1. Существенным требованием к компьютерным ресурсам: RAM, жесткий диск, CPU.

2. Большая продолжительность расчетов и, следовательно, требования к надежности расчетной платформы, ОС и оптимизация использования расчетного оборудования.

3. Широкое использование методов параллельных расчетов.

4. Использование языков высокого уровня Fortran, C/C++.

5. Использование готовых библиотек математических процедур.

6. Требования к повышенной точности расчетов.

Тема подпрограмм: Factor (разложение на множители).

Вариант №14:

Подпрограмма №1: Solve a linear system after factoring (Решение линейной системы после размножения на множители).

Задача: Решите сложную Эрмитову систему линейных уравнений с учетом разложения коэффициентов матрицы вида U∙DU^H.

Для этого используем: CALL LFSHF (N, FAC, LDFAC, IPVT, B, X)

Входные параметры подпрограммы:

1. N — Число уравнений.

2. FAC — Комплексная матрица размерностью NxN, содержащая разложение на множители матрицы коэффициентов A в качестве выходных данных процедуры LFCHF/DLFCHF или LFTHF/DLFTHTHF. Используется только верхний треугольник FAC.

3. LDFAC — ведущее измерение FAC в точности так, как указано в инструкции измерения вызывающей программы.

4. IPVT — вектор длины N, содержащий сводную информацию для факторизации A в качестве выходных данных из процедуры LFCHF/DLFCHF или LFTHF/DLFTHTHF.

5. B — комплексный вектор длины N, содержащий правую часть линейной системы.

Выходные параметры подпрограммы:

1. X — комплексный вектор длины N, содержащий решение линейной системы. Если B не требуется, B и X могут совместно использовать одни и те же места хранения.

Алгоритм.

Процедура LFSHF вычисляет решение системы линейных алгебраических уравнений, имеющих сложную Эрмитову матрицу неопределенных коэффициентов. Чтобы вычислить решение, матрица коэффициентов должна сначала подвергнуться разложению на множители вида U∙DU^H. Это можно сделать, вызвав либо LFCHF, либо LFTHF. LFSHF и LFIHF оба решают линейную систему с учетом ее разложения вида U∙DU^H. LFIHF обычно занимает больше времени и дает более точный ответ, чем FSHF. Каждая итерация алгоритма итерационного уточнения, используемого LFIHF, вызывает LFSHF. LFSHF основан на процедуре LINPACK CSISL.

Пример решения.

Перенесем пример из библиотеки IMSL в систему программирования Fortran и сравним результаты описанные в IMSL и полученные в программе.

Последовательно решается набор линейных систем. Вызывается функция LF HF для разложения матрицы коэффициентов. Вызывается функция FSHF для вычисления трех решений для трех правых частей. В этом случае предполагается, что матрица коэффициентов хорошо подготовлена и правильно масштабирована. В противном случае было бы лучше вызвать LCHF для выполнения факторизации и LFIHF для вычисления решений.

Линкинг – 0 ошибок, 0 предупреждений.

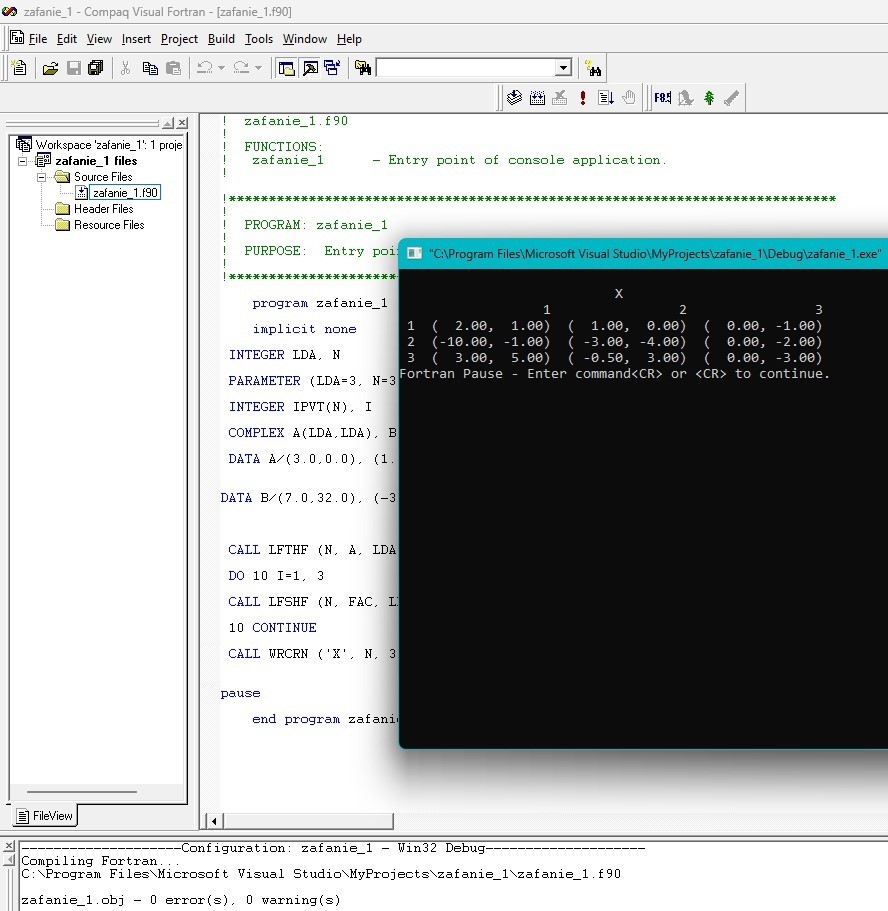
Компиляция – 0 ошибок, 0 предупреждений.

Для наглядности сравним результаты из программы и примера в IMSL.

IMSL:

Fortran:

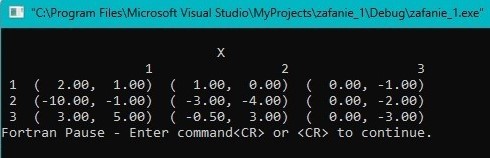
Результаты совпадают.

Подпрограмма №2: High accuracy linear system solution after factoring (Высокоточное линейное системное решение после разложения).

Задача: Используйте итерационное уточнение для улучшения решения сложной Эрмитовой системы линейных уравнений.

Для этого используем: CALL LFIHF (N, A, LDA, FAC, LDFAC, IPVT, B, X, RES)

Входные параметры подпрограммы: