
ЛАБОРАТОРНАЯ РАБОТА № 1. ОПРЕДЕЛЕНИЕ АКТИВНОСТИ ИСТОЧНИКА–ИЗЛУЧЕНИЯ И СРАВНЕНИЕ СТАТИСТИЧЕСКИХ ХРАКТЕРИСТИК ГАЗОРАЗРЯДНОГО И СЦИНТИЛЛЯЦИОННОГО ДЕТЕКТОРОВ
1. Методические основы
Точечный изотропный источник активностью A создает на расстоянии R плотность потока испускаемых им частиц
J |
An |
, |
(1.1) |
|
4 R2 |
||||
|
|
|
где n – выход частиц данного типа (в данной лабораторной работе – -частиц и -излучения), т.е. количество частиц, вылетающих при одном распаде.
Таким образом, измеряя плотность потока J, зная расстояние R и эффективность регистрации детектора по отношению к данному виду излучения , можно определить активность источника излучения. Вообще, расчет по простой формуле
A |
4 R2 J |
(1.2) |
|
n |
|||
|
|
не принимает во внимание ряд обстоятельств, таких как отклонение от изотропии, поглощение излучения в самом источнике и по пути от источника до детектора и т.п. Однако на практике учесть эти факторы достаточно тяжело, поэтому активность, полученная по формуле (1.2), называется
регистрируемой активностью.
В данной лабораторной работе используется определение активности по-излучению, т.е. по регистрации плотности потока электронов от источника 90Sr. В этом случае выход частиц n 1, эффективность регистрации 1.
2. Порядок проведения лабораторной работы
Схема проведения измерений показана на рис. 1.1.
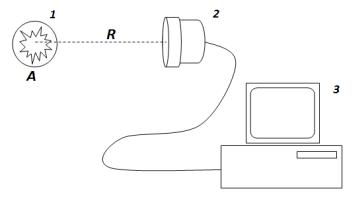
Рис. 1.1. Схема эксперимента: 1 – источник активностью А,
2– детектор излучения,
3– компьютер.
Детектором излучения является дозиметр-спектрометр МКС-15ЭЦ с газоразрядным либо сцинтилляционным блоком детектирования. Результаты экспериментов передаются на компьютер после окончания лабораторной работы.
Проведение лабораторной работы:
Определение активности источника
1.Подготовить дозиметр-спектрометр МКС-15ЭЦ к работе, соединив с электронным пультом газоразрядный блок детектирования.
2.Измерить фоновые значения плотности потока -частиц (10 измерений).
3.Установить источник на расстоянии R = 10 см от блока детектирования. Провести измерения плотности потока (10 повторений).
4.Изменяя положение источника, провести измерения плотности потока -излучения на расстояниях R = 15, 20, 25, 30 и 35 см от детектора излучения.
Измерение статистических характеристик газоразрядного и сцинтилляционного детекторов
1.На электронном пульте дозиметра-спектрометра МКС-15ЭЦ установить время измерения мощности эквивалентной дозы 10 с.
2.Установить источник излучения на расстоянии 5 см от детектора излучения.
3.Провести автоматические измерения мощности эквивалентной дозы в течение 20 мин, что соответствует определению 120 значений дозы.
4.Выключить дозиметр-спектрометр МКС-15ЭЦ. Заменить блок детектирования на сцинтилляционный.
5.Повторить п. 3.
6.Выключить дозиметр-спектрометр МКС-15ЭЦ. Подключить МКС15ЭЦ к компьютеру, включить и сохранить данные измерений.
7.Очистить память МКС-15ЭЦ.
3. Обработка результатов измерений
1.Определить активность источника A по формуле (1.2) для каждого из расстояний 5 – 30 см. Результаты представить в виде таблицы значений.
2.Вычислить погрешность определения величины A.
3.С помощью полученного в п. 1 значения активности построить график теоретической зависимости J(R) (формула (1.1)) и нанести на нее экспериментальные значения.
4.Объяснить полученный результат.
5.Провести статистическую обработку измерений мощности эквивалентной дозы Hi, i=1…N, для обоих детекторов:
а) разбить весь диапазон измеренных значений Hi на k = 10–12 интервалов и построить соответствующую гистограмму, по оси абсцисс которой откладываются значения мощности дозы, по оси ординат – количество измерений ni , i=1…k, попавших в интервал
H значений от H L |
|
до H R |
(левая и правая границы i-го интервала |
|||||||||||||
|
|
|
i |
|
|
|
i |
|
|
|
|
|
|
|
|
|
соответственно); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
k ~ |
~ |
|
|
|
|
|
|
|
|
|
|
|
H |
|
|||||
б) вычислить |
среднее значение |
|
Hi ni , где |
H i |
– среднее |
|||||||||||
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
N i 1 |
|
|
|
значение в i-м интервале; |
|
|
|
|
|
|
|
|
|
|||||||
в) вычислить среднеквадратическое отклонение (СКО) S: |
|
|||||||||||||||
|
1 |
k |
~ |
|
|
|
2 |
|
H |
2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|||||||||
S 2 |
|
n |
H |
i |
H |
|
; |
|
|
|
|
|||||
|
|
|
|
|
|
|||||||||||
|
|
i |
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
N 1 i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
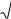
г) в предположении о нормальности распределения рассчитать теоретические вероятности попадания в каждый из k интервалов по
|
|
1 |
|
HiR |
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||
формуле pi |
|
|
|
exp |
|
H H |
dH ; |
|||
|
|
|
|
2 |
|
|||||
|
|
|
||||||||
|
|
2 S HiL |
|
|
2S |
|
|
|||
|
|
|
|
|
|
|
||||
д) рассчитать критерий |
Пирсона соответствия нормальному |
||||
распределению: 2 |
k |
n Np |
|
2 |
|
|
i |
Npi |
i |
; |
|
|
i 1 |
|
|
|
|
е) с помощью полученного значения 2 сделать заключение о том, является полученное распределение нормальным или нет.
