линейная алгебра

Вариант 1

1. Найти произведение матриц

1) не существует 2) 3) 4)

2. Решить систему линейных уравнений с помощью обратной матрицы:

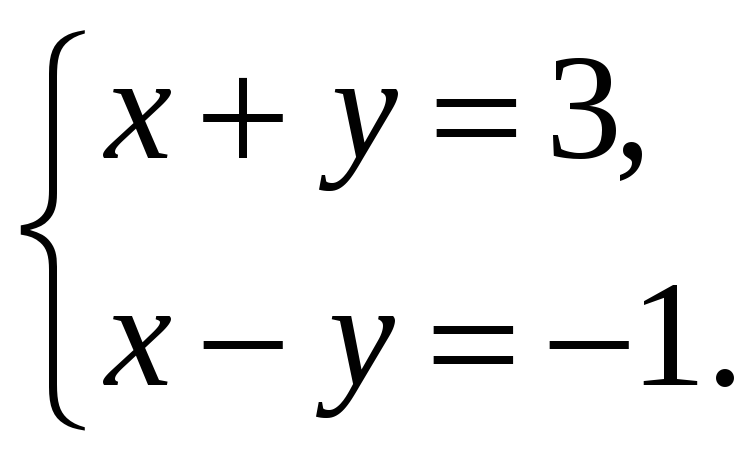
1) не существует 2) 3) 4)

3. Найти решение системы линейных уравнений методом Гаусса:

1) бесконечно много решений 2) 3) нет решения 4)

4. Вычислить , если , , .

1) 51 2) -51 3) 4)

5. Определить какую тройку векторов образуют вектора а(1;–1;3), b(0;3;2), c(–1;1;–1).

1) правая 2) левая 3) вектора компланарны

6. Вычислить , если .

1) 2) 3) 4)

7. Решить уравнение:

.

1) 15 2) 5 3) -5 4) 0

8. Написать уравнение прямой, проходящей через точку А(–2;3) перпендикулярно прямой .

1) 2) 3) 4)

9. Привести уравнение 16x²–9y²–64x–54y–161=0 к каноническому виду и определить тип кривой.

1) 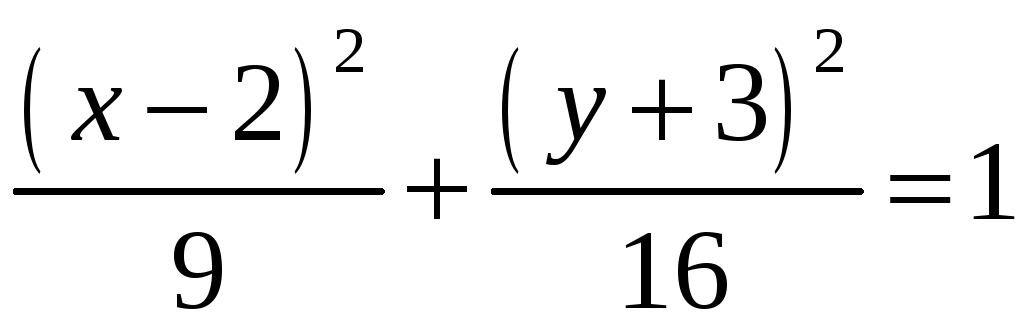2)

3) 4)

10. Записать уравнение плоскости, проходящей через точку А(1;–1;3) перпендикулярно вектору .

1) 2) 3)

4)

Вариант 2

1. Найти произведение матриц

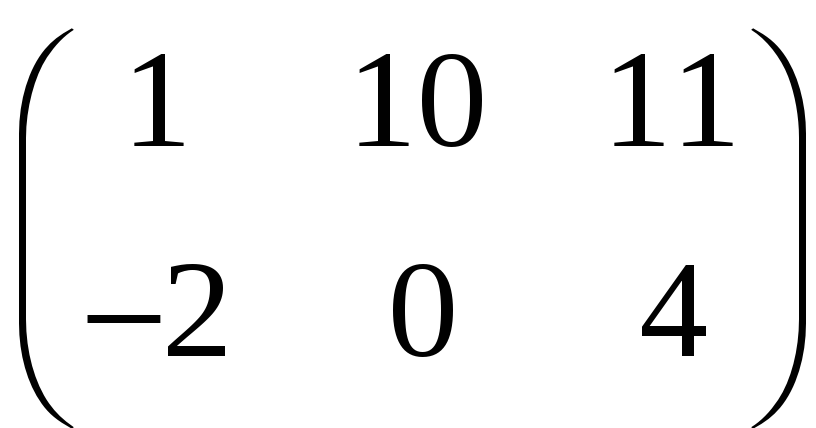1) не существует 2) 3) 4)

2. Решить систему линейных уравнений по формулам Крамера:

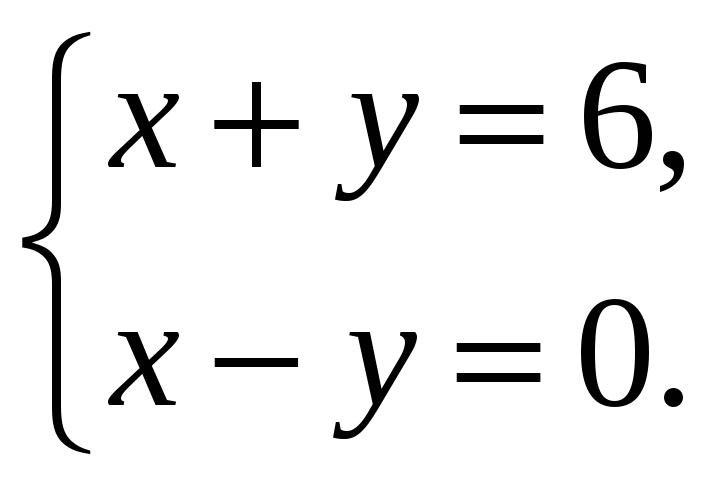
1) не существует 2) 3) 4)

3. Найти решение системы линейных уравнений методом Гаусса:

1) бесконечно много решений 2) 3) нет решения 4)

4. Вычислить , если

1) 7 2) -7 3) 0 4) 18

5. Найти смешанное произведение векторов а(1;–1;3), b(0;3;2), c(–1;1;–1).

1) 12 2) -6 3) 6 4) 15

6. Вычислить , если .

1) 2) 3) 4)

7. Решить неравенство:

.

1) 2) 3) 4)

8. Написать уравнение прямой, проходящей через точку А(2;3) параллельно прямой .

1) 2) 3) 4)

9. Привести уравнение 16x²–9y²–64x–54y–161=0 к каноническому виду и определить тип кривой.

1) парабола 2) эллипс

3) окружность 4) гипербола

10. Записать уравнение плоскости, проходящей через точки

1) 2) 3)

4)

Вариант 3

1. Найти произведение матриц

1) не существует 2) 3) 4)

2. Решить систему линейных уравнений с помощью обратной матрицы:

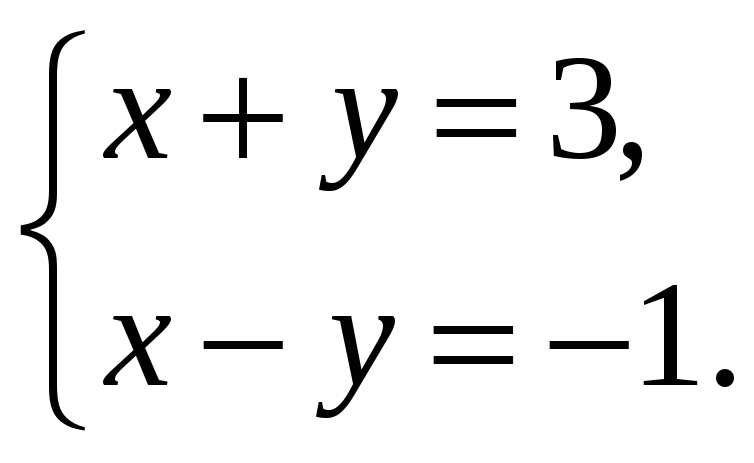
1) не существует 2) 3) 4)

3. Найти решение системы линейных уравнений методом Гаусса:

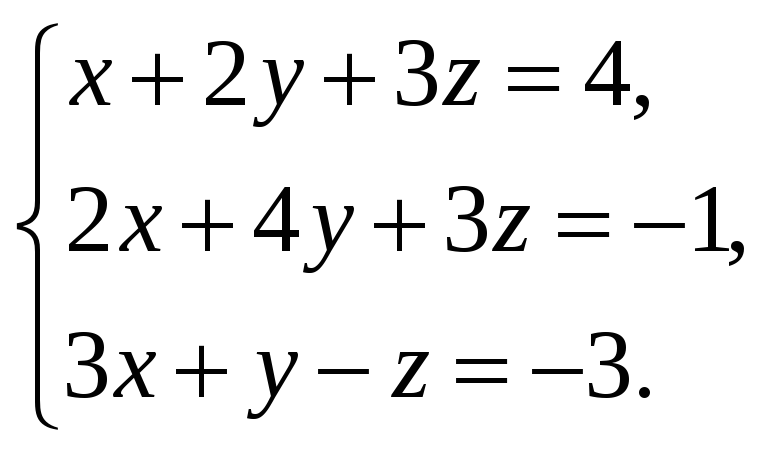
1) бесконечно много решений 2) 3) нет решения 4)

4. Вычислить , если , , .

1) 51 2) -51 3) 4)

5. Определить какую тройку векторов образуют вектора а(1;–1;3), b(0;3;2), c(–1;1;–1).

1) правая 2) левая 3) вектора компланарны

6. Вычислить , если .

1) 2) 3) 4)

7. Решить неравенство:

.

1) 2) 3) 4)

8. Написать уравнение прямой, проходящей через точку А(2;3) параллельно прямой .

1) 2) 3) 4)

9. Привести уравнение 16x²–9y²–64x–54y–161=0 к каноническому виду и определить тип кривой.

1) парабола 2) эллипс

3) окружность 4) гипербола

10. Записать уравнение плоскости, проходящей через точки

1) 2) 3)

4)

Вариант 4

1. Найти произведение матриц

1) не существует 2) 3) 4)

2. Решить систему линейных уравнений по формулам Крамера:

1) не существует 2) 3) 4)

3. Найти решение системы линейных уравнений методом Гаусса:

1) бесконечно много решений 2) 3) нет решения 4)

4. Вычислить , если

1) 7 2) -7 3) 0 4) 18

5. Найти смешанное произведение векторов а(1;–1;3), b(0;3;2), c(–1;1;–1).

1) 12 2) -6 3) 6 4) 15

5. Определить какую тройку векторов образуют вектора а(1;–1;3), b(0;3;2), c(–1;1;–1).

1) правая 2) левая 3) вектора компланарны

6. Вычислить , если .

1) 2) 3) 4)

7. Решить уравнение:

.

1) 15 2) 5 3) -5 4) 0

8. Написать уравнение прямой, проходящей через точку А(–2;3) перпендикулярно прямой .

1) 2) 3) 4)

9. Привести уравнение 16x²–9y²–64x–54y–161=0 к каноническому виду и определить тип кривой.

1) 2)

3) 4)

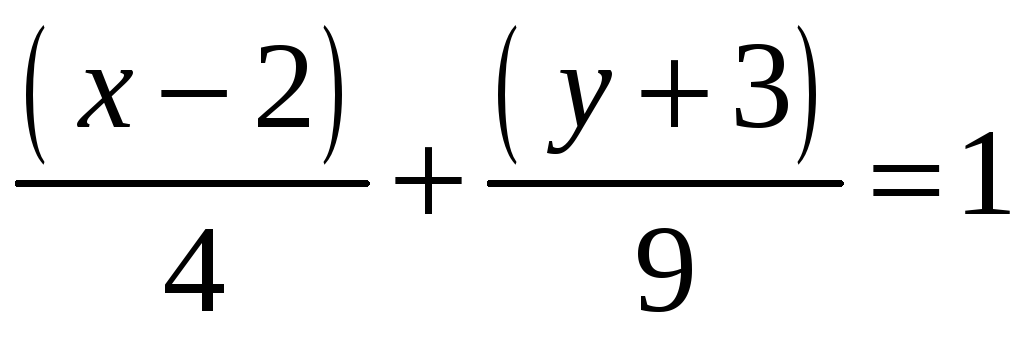
10. Записать уравнение плоскости, проходящей через точку А(1;–1;3) перпендикулярно вектору .

1) 2) 3)

4)