
Lab5 / ИССЛабораторная №5
.docxЛабораторная работа №5
Кластеризация с помощью Python
Цель работы: Кластеризация с помощью Python
Задание:
1. По примеру выполнить кластеризацию цветного изображения, изображения взять произвольно.
2. Оптимизировать параметры кластеризации, до тех пора пока все цвета не будут выделяться корректно.
Ход работы
Шаг 1. Инициализация библиотек
В Colab для загрузки изображение использовали следующий код:

Шаг 2. Преобразования изображения в матрицу

Шаг 3. Настройка модели Kmeans.

Шаг 4. Применение кластеризации

Шаг 5. Восстановление изображения

Шаг 6. Визуализации изображения

Шаг 7. Функция для определения кластера по пикселю на изображении
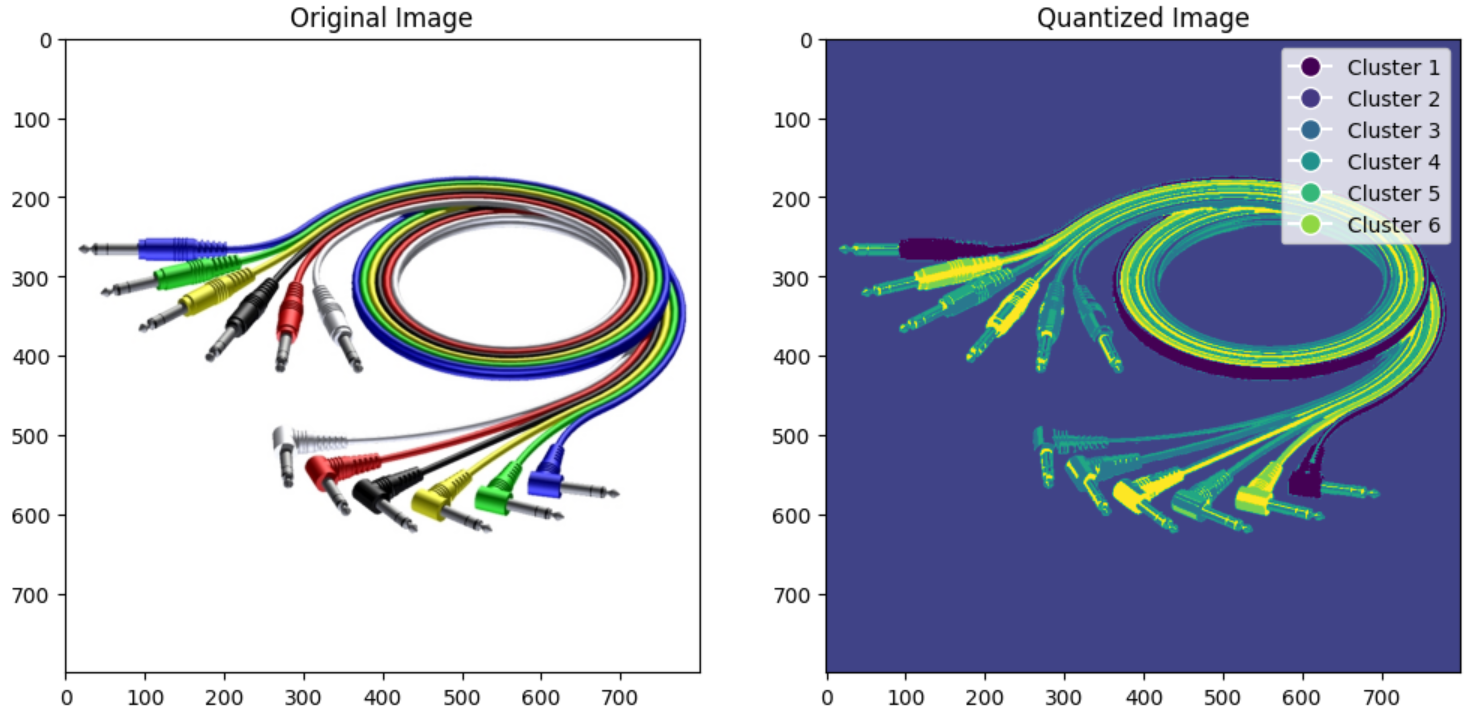
Рисунок 1 – Результат кластеризации
Рисунок был разбит на 5 кластеров соответствующий каждый своему цвету. Увидеть определение кластера можно в правом верхнем углу окна figure.
1) Изменить параметр n_colors следующим образом - увеличить его на 2, уменьшить на 2, увеличить на 10.
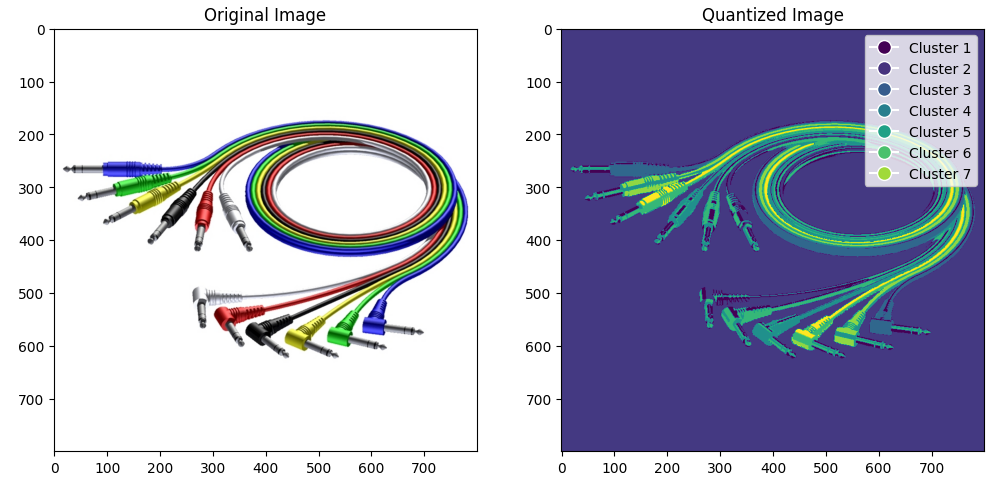 Рисунок 2 – n_colors
увеличили на 2
Рисунок 2 – n_colors
увеличили на 2
Появилось больше оттенков на изображение.
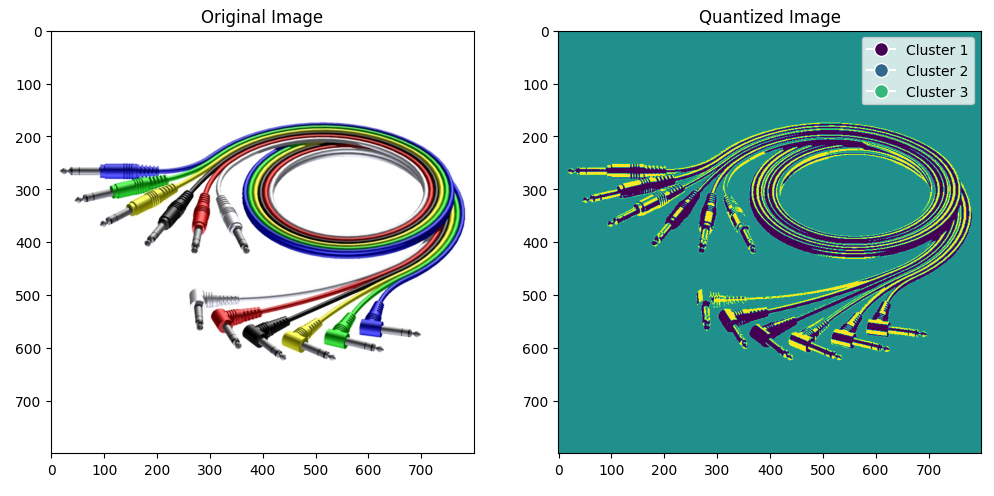
Рисунок 3 – n_colors уменьшили на 2
Цвета стали слабо калечимы. Уменьшилась детализация изображения.
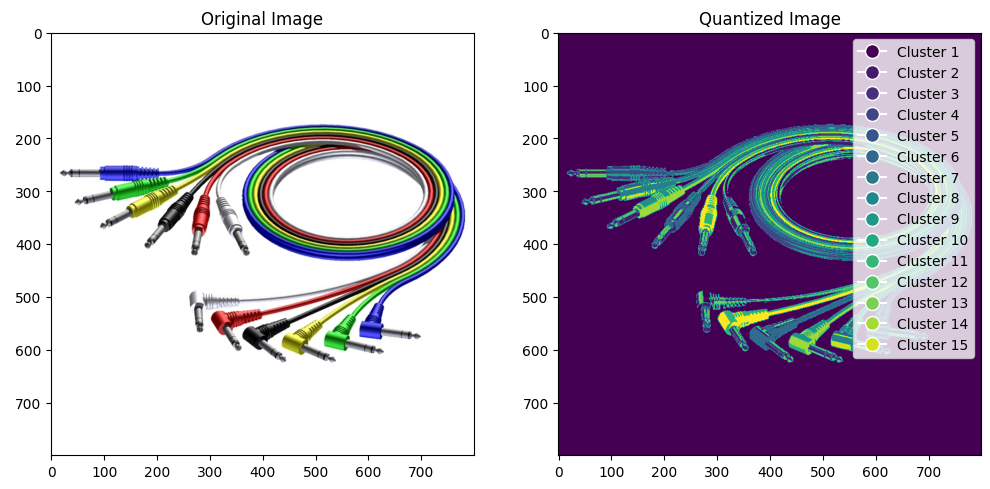
Рисунок 4 – n_colors увеличили на 10
Появились похожие оттенки. Увеличилась детализация изображения.
2) Изменить параметр sample_size следующим образом – сделать его равным n_colors, увеличить в 10 раз, уменьшить в 10 раз. (Если samplesize после уменьшение стал меньше n_colors, уменьшите его так чтобы выполнялось условие n_colors <= sample_size
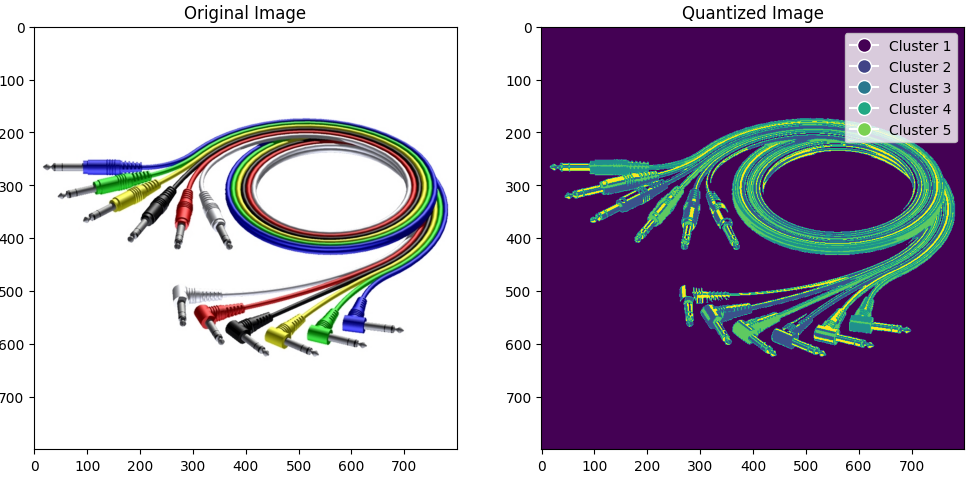
Рисунок 5 – sample_size увеличили в 10
Заметны различия в цветах.
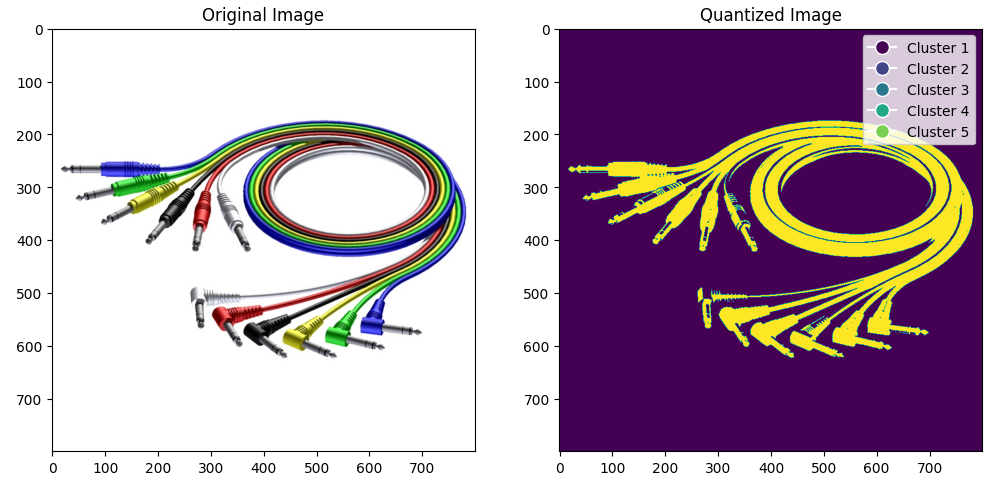
Рисунок 6 – sample_size уменьшили в 10
Из-за уменьшения выборки кластеризация стала почти однотонной
3) С помощью метода локтя определить оптимальное значение количества кластеров.
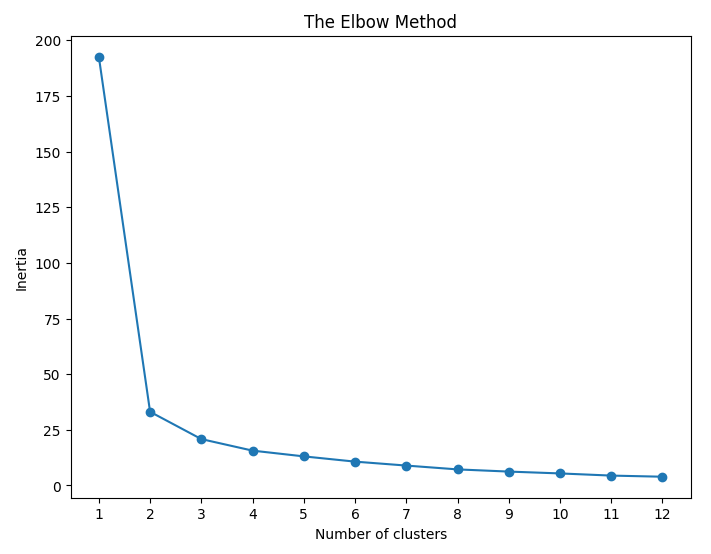
Рисунок 7 –Метод локтя
На рисунке 7 выделили два значения кластера, это 4 и 5, последнее число как раз соответствуют реальному значению кластеров.
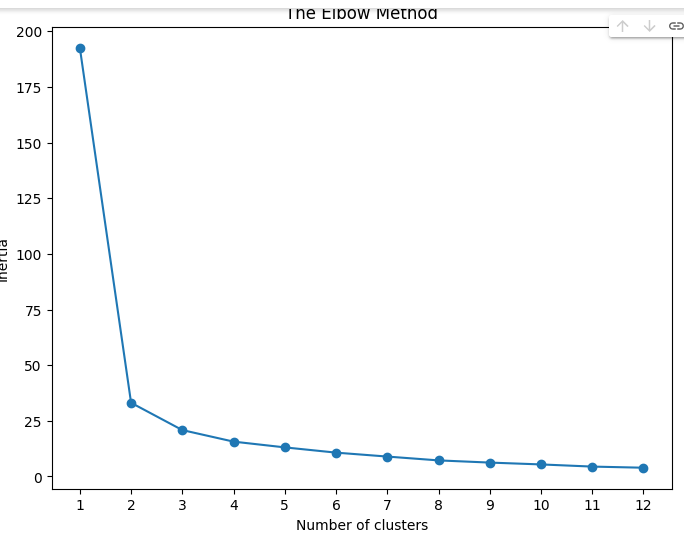
4) С помощью np.diff возьмите вторую производную значений оценки инерции. Сравните с результатом полученным в пункте 3.
# Получение первой производной
inertia_diff1 = np.diff(inertia_values)
# Получение второй производной
inertia_diff2 = np.diff(inertia_diff1)
# Визуализация второй производной метода "локтя"
plt.figure(figsize=(8, 6))
plt.plot(range(3, max_clusters + 1), inertia_diff2, marker='o')
plt.xlabel('Number of clusters')
plt.ylabel('Second Derivative of Inertia')
plt.title('Second Derivative of The Elbow Method')
plt.xticks(range(3, max_clusters + 1))
plt.show()
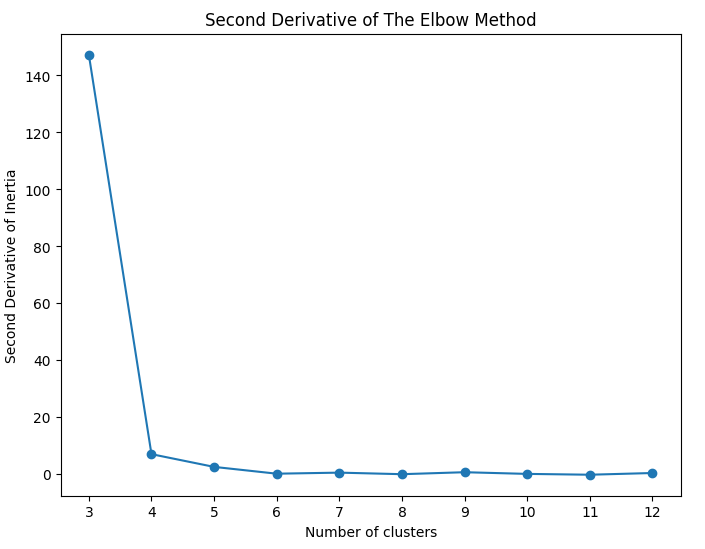
На 4 кластере происходит резкое изменение, в отличие от графика в пункте 3.
Листинг программы:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.utils import shuffle
from PIL import Image
from google.colab import files
# Загрузка изображения
uploaded = files.upload()
for filename in uploaded.keys():
image = Image.open(filename)
image = np.array(image, dtype=np.float64) / 255
# Преобразование изображения в 2D массив
w, h, d = original_shape = tuple(image.shape)
image_array = np.reshape(image, (w * h, d))
# Настройка модели KMeans
n_colors = 5
sample_size = 1000
image_array_sample = shuffle(image_array, random_state=0)[:sample_size]
# Исправлено: явное задание параметра n_init
kmeans = KMeans(n_clusters=n_colors, n_init=10, random_state=0)
# Применение кластеризации
kmeans.fit(image_array_sample)
labels = kmeans.predict(image_array)
# Восстановление изображения
quantized_image = np.reshape(labels, (w, h))
# Визуализация исходного и кластеризованного изображения
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 6))
# Визуализация оригинального изображения слева
ax1.imshow(image)
ax1.set_title('Original Image')
# Визуализация кластеризованного изображения справа
ax2.imshow(quantized_image, cmap=plt.cm.viridis)
ax2.set_title('Quantized Image')
# Создание легенды
legend_elements = []
for i in range(n_colors):
legend_elements.append(plt.Line2D([0], [0], marker='o', color='w', label=f'Cluster {i+1}', markersize=10, markerfacecolor=plt.cm.viridis(i/n_colors)))
# Добавление легенды
ax2.legend(handles=legend_elements, loc='upper right')
plt.show()
def onclick(event):
if event.inaxes == ax2:
x = int(event.xdata)
y = int(event.ydata)
cluster = quantized_image[y, x]
ax2.set_title(f'Cluster: {cluster}')
fig.canvas.mpl_connect('motion_notify_event', onclick)
# Определение оптимального числа кластеров с использованием метода "локтя"
inertia_values = []
max_clusters = 12
for n_clusters in range(1, max_clusters + 1):
# Исправлено: явное задание параметра n_init
kmeans = KMeans(n_clusters=n_clusters, n_init=10, random_state=0)
kmeans.fit(image_array_sample)
inertia_values.append(kmeans.inertia_)
# Визуализация метода "локтя"
plt.figure(figsize=(8, 6))
plt.plot(range(1, max_clusters + 1), inertia_values, marker='o')
plt.xlabel('Number of clusters')
plt.ylabel('Inertia')
plt.title('The Elbow Method')
plt.xticks(range(1, max_clusters + 1))
plt.show()
Вывод: в ходе лабораторной работы ознакомились с кластеризацией с помощью Python.
