книги2 / монография 33

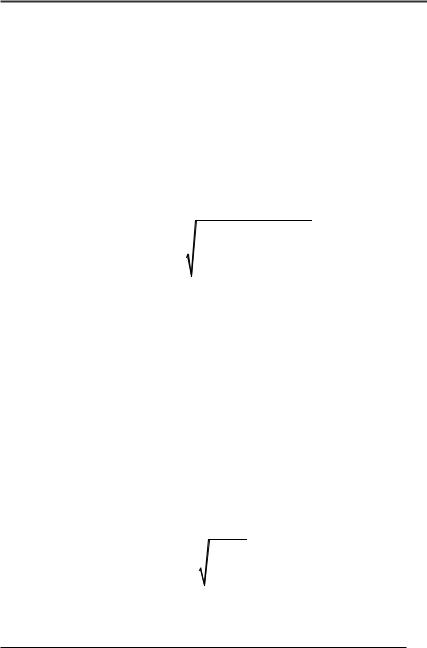
Синергетическая теория целостности

Эти условия являются естественными, т. е. они характеризуют процессы, происходящие в живой и неживой природе совершенно естественным образом [81]. Только человек может, например, сознательно нарушить условие 2.

Далее мы будем изучать именно такие процессы.

Принято считать, что когда совокупность условий (1–3) выполняется, выборки

Bj; j = 1..n

описываются законом распределения вероятностей Стьюдента [81]. Обозначим

Пусть τj* — критическое значение критерия Стьюдента при заданной доверительной вероятности P* и степени свободы

(Nj− 1):

В случае справедливости распределения вероятностей Стьюдента можно оперировать следующими противоположными неравенствами:

Обозначим

31

А. П. Хускивадзе

1.5 Истина и вероятностный предел ее познания

Говорят, что в момент времени t = t0 МР S является заданной (определенной, известной) с вероятностью, равной 1, если задана совокупность

Mj(G); j = 1..n,

где Mj(G) — генеральное среднее арифметическое случайной вели-

чины Mj.

Если эта совокупность генеральных средних величин в момент времени t = t0 является известной, то говорят, что в этот момент времени истина в МР S познана с вероятностью, равной единице.

Обозначим через P вероятность того, что выполняется условие

Mj = Mj(G) для всех j = 1..n

О величине P говорят, что она является вероятностью фак-

тического познания истины в МР S в момент времени t = t0.

Согласно (1.6) и (1.9), имеет место

│Mj − Mj(G)│< j*; j = 1..n

Эта запись имеет смысл в том и только в том случае, когда

j

Из (1.7), (1.9) и (1.10) имеем

|Mj − Mj(G)| ≥ j*> 0; j = 1..n

Отсюда следует, что вообще

32

Синергетическая теория целостности

Mj ≠ Mj(G); j = 1..n

Следовательно, в этом случае не может быть речи о выполнении условия

А величина P по определению является вероятностью выполнения именно этого условия.

В итоге

P < 1 при |Mj − Mj(G)| ≥ j*> 0; j = 1..n

Пусть теперь имеет место

│Mj − Mj(G)│<  j*; j = 1..n

Обозначим через Pj вероятность того, что истиной является утверждение:

Mj = Mj(G) при │Mj − Mj(G)│<  j*; j = j0; j0 = 1..n

Вообще

Pj ≤ P* ≡ (1 − α); j = 1..n,

где α — заданный уровень значимости.

Следовательно, в лучшем случае будет иметь место

Pj = (1 − α); j = 1..n

В таблице критических точек распределения вероятностей Стьюдента [82, с. 466] приведены следующие значения величины α:

α1= 0,05; α2 = 0,025; α3 = 0,01; α4 = 0,005; α5 = 0,001 и α6 = 0,0005

Как видно,

α ≥ 5.10–4

33

А. П. Хускивадзе

Таким образом, если будем считать, что вышеуказанная таблица является полной, то можно написать

αmin = 5.10–4  > 0,

где αmin— минимально возможное значение α.

Предположим, что вышеуказанная таблица не является полной. Положим, что в ней нет тех критических точек, для которых имеет место

α< 5.10–4

Вэтом случае придется создать новую — расширенную — таблицу. Эта таблица должна содержать в себе все семь столбцов вышеуказанной таблицы и плюс один или более новых столбцов.

Обозначим через αN то искомое значение α, которое должно быть внесено в N-м столбце расширенной таблицы, где N — натуральное число, такое, что

N ≥ 7

Вышеприведенные значения величины α, как видно, такие, что выполняется условие

α1 > α2> α3> α4>α5> α6

Это условие будет выполняться и во всех новых столбцах расширенной таблицы, если положим, что вообще

αN = 10–(N – 3)bN,

где bN — вещественное число, такое, что

bN = 5 при N = 7

0 < bN < 5 при 7 < N < +∞ bN → 0 при N → ∞

В самом деле, легко проверить, что

34

Синергетическая теория целостности

αN = 5 .10–4 при N = 7 αN > 0 при 7 < N < +∞

αN = 0 при N = + ∞

Случай, когда N = +∞, является нереализуемым. Реализуемыми являются только те случаи, когда имеет место N < +∞.

Аво всех этих случаях, как только что видели, имеет место

α≥ αmin > 0

Витоге всегда выполняется условие [73–75, 78, 79]:

Отметим, что справедливость неравенства, аналогичного по смыслу неравенству (1.10), в физике впервые была постулирована Гейзенбергом. Этот постулат известен, как Принцип неопределенности Гейзенберга. Считают, что он является одним из фундаментальных принципов неживой природы [83]. Область справедливости неравенства (1.10) шире. Она охватывает не только

неживую, но живую природу.

Следует также отметить, что положение о невозможности познания истины с вероятностью, равной 1, в философии известно давно [84]. А в математической логике это положение, по сути дела, было доказано еще в конце 20-х годов прошлого столетия [85, 86]. Выше мы еще раз подтвердили справедливость этого положения. Точнее, мы показали, что оно справедливо по крайней мере для тех явлений природы, которые описываются распределением вероятностей Стьюдента.

35

А.П. Хускивадзе

1.6Локальные единицы измерения показателей качества функционирования МР

Пусть P0 — наибольшее возможное значение P для МР S при

t = t0. О величине P0 говорят, что она является вероятностным пределом познания истины МР S при t = t0.

Вообще, как увидим в параграфе 3.3, имеет место

36

Синергетическая теория целостности

Величины (1.17) для каждой МР S можно установить по результатам ее обследования. В главе 5 мы увидим, что по тем же результатам обследования МР S можно установить и величины (1.18).

Согласно (1.15) и (1.19), имеет место

Положим, что известными являются выборки:

Bj1 = { bjλ1 ; λ = 1…Nj1} и Bj0 = { bjλ0 ; λ = 1... Nj0}; j = 1..n,

где

Bj1 — выборка данных, по которой установлена пара (Mj1, Sj1); Bj0 — выборка данных, по которой установлена пара (Mj0, Sj0). Положим также, что для этих выборок выполняются условия 1–3. Тогда, как указывалось выше, можно оперировать распределе-

нием Стьюдента.

37

А. П. Хускивадзе

Обозначим

j= 1..n,

где τj — критическое значение критерия Стьюдента при доверительной вероятности P и степени свободы (Nj0 + Nj1− 2).

Принимая во внимание, что P > 0, из (1.20) и (1.21) получаем

В итоге для каждого j всегда имеет место одно из следующих неравенств:

Если выполняется условие (1.24), то с вероятностью P утверждают, что справедливо равенство:

Mj1 = Mj0; j = j0; j0 = 1..n

Тем самым полагают, что в каждой открытой области

Aj(откр.) = (Mj0 − σj, Mj0 + σj); j = j0; j0 = 1..n

все значения величины Mj1 являются практически неразличимыми от Mj0.Вместе с тем в каждой закрытой области

38

Синергетическая теория целостности

Aj(закр.) = [Mj0 − σj, Mj0 + σj)]; j = j0; j0 = 1..n,

друг от друга различаются следующие три значения величины Mj1:

Mj1 = Mj0 − σj; Mj1 = Mj0 и Mj1 = Mj0 + σj ; j = j0; j0 = 1..n

Это означает, что каждую величину yj в области Aj(закр.)

наиболее точно можно измерить в единицах σj и только в них.

Но если в области Aj(закр.) величину yj мы будем измерять в единицах σj, то в этих же единицах мы должны ее измерить и в остальной части области задания величины yj. В противном случае будет нарушено условие равноточности измерений.

Таким образом, в том случае, когда имеет место (1.22), каждую величину yj наиболее точно можно измерить не в единицах ∆yj, а в единицах σj ≥ ∆yj, где ∆yj — абсолютная ошибка измерительного прибора величины yj.

Итак, в том случае, когда оперируют неравенствами (1.24) и (1.25), величины (1.1) наиболее точно можно измерить в единицах (1.22).

Следовательно, в этих же единицах наиболее точно можно измерить и величины

где σj0 — минимально возможное значение σj для МР S в момент

времени t = t0.

Вообще, согласно (1.16), (1.21) и (1.26), имеет место

39

А.П. Хускивадзе

1.7Понятие нормального состояния материальной реальности

то с вероятностью P можно утверждать, что

Mj1 = Mj0 для всех j = 1..n

И это утверждение будет тем ближе к истине, чем меньшими будут величины (1.22).

Величины (1.22), согласно (1.27), являются наименьшими в том и только в том случае, когда имеет место равенство

Следовательно, наиболее близко к истине вышеприведенное утверждение будет в том и только в том случае, когда имеет место равенство (1.29).

Равенство (1.29), согласно (1.26), имеет место в том случае, когда

В итоге наиболее близко к истине вышеприведенное утверждение будет в том и только в том случае, когда имеет место (1.30), что вполне логично.

Можно показать, что в том случае, когда имеет место (1.30), всегда выполняется условие

В самом деле, когда имеет место равенство (1.30), согласно (1.26), всегда имеет место и равенство (1.29). А с учетом равенства

(1.29) из (1.28) получаем (1.31).

40