типовой

ВАРИАНТ 1

1. Используя интеграл Лапласа, найти изображение функции

2. Используя функцию Хевисайда и теорему запаздывания, найти изображение функции, заданной графиком

3. Используясвойства преобразования Лапласа и таблицу изображений, найти изображения функций:

1. ; б) .

4. Используя свойства преобразования Лапласа и разложение на простейшие дроби, найти оригиналы функций:

а) ;б) .

5. Применяя операционное исчисление, найти частное решение дифференциального уравнения

.

6.Применяя операционное исчисление,вычислить несобственный интеграл

ВАРИАНТ 2

1. Используя интеграл Лапласа, найти изображение функции

2. Используя функцию Хевисайда и теорему запаздывания, найти изображение функции, заданной графиком

3. Используя свойства преобразования Лапласа и таблицу изображений, найти изображения функций:

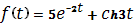1. ; б) .

4. Используя свойства преобразования Лапласа и разложение на простейшие дроби, найти оригиналы функций:

а) ;б) .

5. Применяя операционное исчисление, найти частное решение дифференциального уравнения

.

6. Применяя операционное исчисление, вычислить несобственный интеграл

ВАРИАНТ 3

1. Используя интеграл Лапласа, найти изображение функции

2. Используя функцию Хевисайда и теорему запаздывания, найти изображение функции, заданной графиком

3. Используя свойства преобразования Лапласа и таблицу изображений, найти изображения функций:

1. ; б) .

4. Используя свойства преобразования Лапласа и разложение на простейшие дроби, найти оригиналы функций:

а) ;б) .

5. Применяя операционное исчисление, найти частное решение дифференциального уравнения

.

6. Применяя операционное исчисление, вычислить несобственный интеграл

ВАРИАНТ 4

1. Используя интеграл Лапласа, найти изображение функции

2. Используя функцию Хевисайда и теорему запаздывания, найти изображение функции, заданной графиком

3. Используя свойства преобразования Лапласа и таблицу изображений, найти изображения функций:

1. ; б) .

4. Используя свойства преобразования Лапласа и разложение на простейшие дроби, найти оригиналы функций:

а) ;б) .

5. Применяя операционное исчисление, найти частное решение дифференциального уравнения

.

6. Применяя операционное исчисление, вычислить несобственный интеграл

ВАРИАНТ 5

1. Используя интеграл Лапласа, найти изображение функции

2. Используя функцию Хевисайда и теорему запаздывания, найти изображение функции, заданной графиком

3. Используя свойства преобразования Лапласа и таблицу изображений, найти изображения функций:

1. ; б) .

4. Используя свойства преобразования Лапласа и разложение на простейшие дроби, найти оригиналы функций:

а) ;б) .

5. Применяя операционное исчисление, найти частное решение дифференциального уравнения

.

6. Применяя операционное исчисление, вычислить несобственный интеграл

ВАРИАНТ 6

1. Используя интеграл Лапласа, найти изображение функции

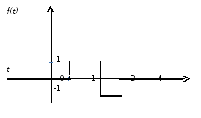
2. Используя функцию Хевисайда и теорему запаздывания, найти изображение функции, заданной графиком

3. Используя свойства преобразования Лапласа и таблицу изображений, найти изображения функций:

1. ; б) .

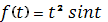4. Используя свойства преобразования Лапласа и разложение на простейшие дроби, найти оригиналы функций:

а) ;б) .

5. Применяя операционное исчисление, найти частное решение дифференциального уравнения

.

6. Применяя операционное исчисление, вычислить несобственный интеграл

ВАРИАНТ 7

1. Используя интеграл Лапласа, найти изображение функции

2. Используя функцию Хевисайда и теорему запаздывания, найти изображение функции, заданной графиком

3. Используя свойства преобразования Лапласа и таблицу изображений, найти изображения функций:

1. ; б) .

4. Используя свойства преобразования Лапласа и разложение на простейшие дроби, найти оригиналы функций:

а) ;б) .

5. Применяя операционное исчисление, найти частное решение дифференциального уравнения

.

6. Применяя операционное исчисление, вычислить несобственный интеграл

ВАРИАНТ 8

1. Используя интеграл Лапласа, найти изображение функции

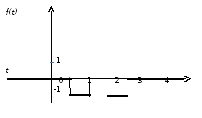
2. Используя функцию Хевисайда и теорему запаздывания, найти изображение функции, заданной графиком

3. Используя свойства преобразования Лапласа и таблицу изображений, найти изображения функций:

1. ; б) .

4. Используя свойства преобразования Лапласа и разложение на простейшие дроби, найти оригиналы функций:

а) ;б) .

5. Применяя операционное исчисление, найти частное решение дифференциального уравнения

.

6. Применяя операционное исчисление, вычислить несобственный интеграл

ВАРИАНТ 9

1. Используя интеграл Лапласа, найти изображение функции

2. Используя функцию Хевисайда и теорему запаздывания, найти изображение функции, заданной графиком

3. Используя свойства преобразования Лапласа и таблицу изображений, найти изображения функций:

1. ; б) .

4. Используя свойства преобразования Лапласа и разложение на простейшие дроби, найти оригиналы функций:

а) ;б) .

5. Применяя операционное исчисление, найти частное решение дифференциального уравнения

.

6. Применяя операционное исчисление, вычислить несобственный интеграл

ВАРИАНТ 10

1. Используя интеграл Лапласа, найти изображение функции

.

2. Используя функцию Хевисайда и теорему запаздывания, найти изображение функции, заданной графиком

3. Используя свойства преобразования Лапласа и таблицу изображений, найти изображения функций:

1. ; б) .

4. Используя свойства преобразования Лапласа и разложение на простейшие дроби, найти оригиналы функций:

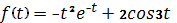а) ;б) .

5. Применяя операционное исчисление, найти частное решение дифференциального уравнения

.

6. Применяя операционное исчисление, вычислить несобственный интеграл

ВАРИАНТ 11

1. Используя интеграл Лапласа, найти изображение функции

2. Используя функцию Хевисайда и теорему запаздывания, найти изображение функции, заданной графиком

3. Используя свойства преобразования Лапласа и таблицу изображений, найти изображения функций:

1. ; б) .

4. Используя свойства преобразования Лапласа и разложение на простейшие дроби, найти оригиналы функций:

а) ;б) .

5. Применяя операционное исчисление, найти частное решение дифференциального уравнения

.

6. Применяя операционное исчисление, вычислить несобственный интеграл

ВАРИАНТ 12

1. Используя интеграл Лапласа, найти изображение функции

2. Используя функцию Хевисайда и теорему запаздывания, найти изображение функции, заданной графиком

3. Используя свойства преобразования Лапласа и таблицу изображений, найти изображения функций:

1. ; б) .

4. Используя свойства преобразования Лапласа и разложение на простейшие дроби, найти оригиналы функций:

а) ;б) .

5. Применяя операционное исчисление, найти частное решение дифференциального уравнения

.

6. Применяя операционное исчисление, вычислить несобственный интеграл

ВАРИАНТ 13

1. Используя интеграл Лапласа, найти изображение функции

2. Используя функцию Хевисайда и теорему запаздывания, найти изображение функции, заданной графиком

3. Используя свойства преобразования Лапласа и таблицу изображений, найти изображения функций:

1. ; б) .

4. Используя свойства преобразования Лапласа и разложение на простейшие дроби, найти оригиналы функций:

а) ;б) .

5. Применяя операционное исчисление, найти частное решение дифференциального уравнения

.

6. Применяя операционное исчисление, вычислить несобственный интеграл

ВАРИАНТ 14

1. Используя интеграл Лапласа, найти изображение функции

2. Используя функцию Хевисайда и теорему запаздывания, найти изображение функции, заданной графиком

3. Используя свойства преобразования Лапласа и таблицу изображений, найти изображения функций:

1. ; б) .

4. Используя свойства преобразования Лапласа и разложение на простейшие дроби, найти оригиналы функций:

а) ;б) .

5. Применяя операционное исчисление, найти частное решение дифференциального уравнения

.

6. Применяя операционное исчисление, вычислить несобственный интеграл

ВАРИАНТ 15

1. Используя интеграл Лапласа, найти изображение функции

2. Используя функцию Хевисайда и теорему запаздывания, найти изображение функции, заданной графиком

3. Используя свойства преобразования Лапласа и таблицу изображений, найти изображения функций:

1. ; б) .

4. Используя свойства преобразования Лапласа и разложение на простейшие дроби, найти оригиналы функций:

а) ;б) .

5. Применяя операционное исчисление, найти частное решение дифференциального уравнения

.

6. Применяя операционное исчисление, вычислить несобственный интеграл

ВАРИАНТ 16

1. Используя интеграл Лапласа, найти изображение функции

2. Используя функцию Хевисайда и теорему запаздывания, найти изображение функции, заданной графиком

3. Используя свойства преобразования Лапласа и таблицу изображений, найти изображения функций:

1. ; б) .

4. Используя свойства преобразования Лапласа и разложение на простейшие дроби, найти оригиналы функций:

а) ;б) .

5. Применяя операционное исчисление, найти частное решение дифференциального уравнения

.

6. Применяя операционное исчисление, вычислить несобственный интеграл