4.4 Особенности измерения допплеровской частоты при счп

В режиме СЧП, наблюдается неоднозначность в определении и допплеровских частот сигналов, отраженных от цели, т.е. кроме «слепых» дальностей имеются и «слепые» зоны по частоте. Для разрешения неоднозначности измерения допплеровских частот и устранения «слепых» зон также применяется несколько ЧПИ в последовательно излучаемых пачках импульсов, как и при разрешении неоднозначности по дальности.

«Наблюдаемую» доплеровскую частоту определяют по номеру фильтра в пределах интервала фильтрации, равного обычно частоте повторения импульсов. На рисунке 4.9 показаны зависимости наблюдаемой доплеровской частоты при двух ЧПИ от значения истинной доплеровской частоты цели (при сближении с целью). Можно составить для этого случая два уравнения:

(4.56)

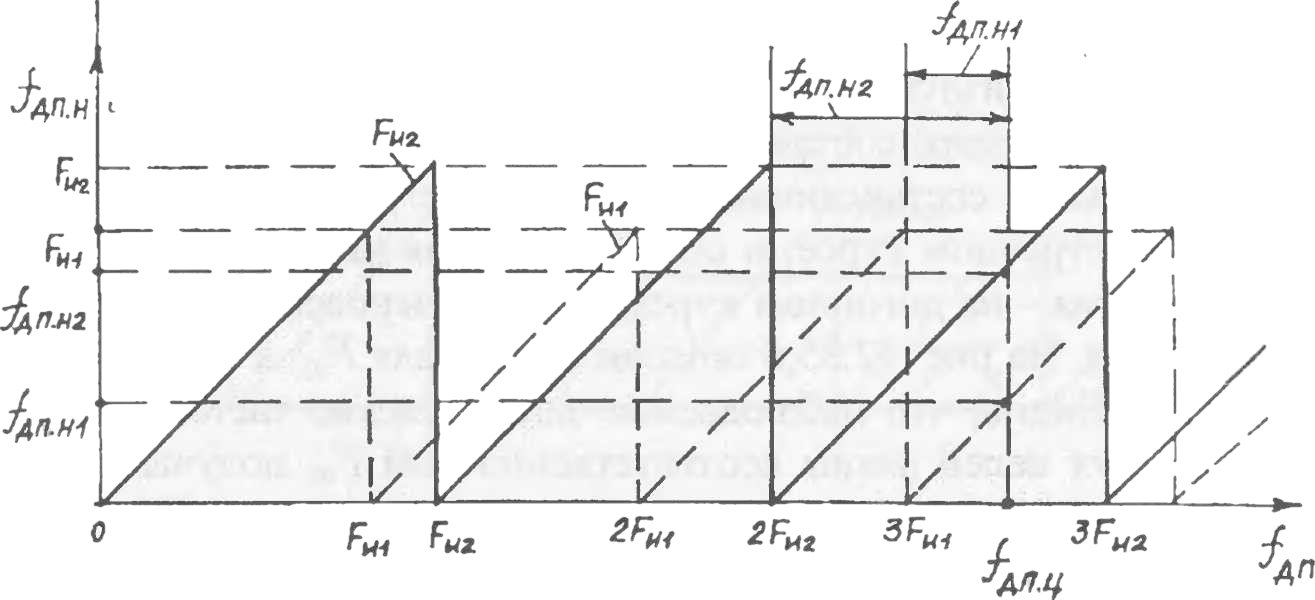
Рисунок 4.9  Зависимости наблюдаемой допплеровской частоты при двух ЧПИ от значения истинной допплеровской частоты цели (при сближении с целью)

где m и n– целые числа интервалов однозначных измерений наблюдаемых частот. Эти интервалы количественно соответствуют частотам повторения и .

По внешнему виду уравнения (4.56) соответствуют аналогичным уравнениям для определения истинного расстояния до цели при неоднозначных измерений при СЧП (см. уравнения (4.24) и (4.25)). Способы решения уравнения (4.56) совершенно аналогичны, рассмотренным ранее, и здесь мы их повторять не будем.

Обратим внимание на то, что изменение ЧПИ позволяет также раскрывать «слепые» зоны по доплеровским частотам. Действительно, из рисунка 4.9 следует, что если наблюдаемая доплеровская частота при одной ЧПИ ( ) равна нулю (совпадает со «слепой» зоной, кратной ЧПИ), то на другой ЧПИ (например, ) наблюдаемая доплеровская час юта уже не равна нулю и выходит из «слепой» зоны.

В ряде случаев, по техническим причинам, целесообразно зону фильтрации выбирать между спектральными составляющими МО по главному лучу (ГЛ). Зона МО по главному лучу является “слепой” для обнаружения. Зоны фильтрации выбирают между составляющими МО по ГЛ, что позволяет полностью использовать все фильтры для обнаружения целей.

В связи с таким выбором зоны фильтрации возникают некоторые особенности в методике устранения неоднозначностей и в оценке допплеровских частот отраженных от цели сигналов. Для иллюстрации сказанного на рисунке 4.10 показаны примеры спектров отраженных сигналов для режима СЧП для двух ЧПИ, равных =15 кГц и =18 кГц. На рисунке 4.10,а показан спектр отражений для одной излучаемой частоты (одной спектральной линии) на частоте . Показаны составляющая МО по ГЛ (частота =36 кГц) и спектральные составляющие отражений от двух целей: одна движется на встречном курсе, и ее допплеровская частота равна =60 кГц, а другая - на догонном курсе, и ее допплеровская частота равна =12 кГц. На рисунке 4.10,6 показан спектр для , а на рисунке 4.10,в - для . Видно, что наблюдаемые допплеровские частоты для указанных двух целей равны соответственно: для получаем  =9 кГц для первой цели Ц1 и  =6 кГц - для второй цели Ц2.

Аналогично получаем при : наблюдаемая допплеровская частота для первой цели  =6 кГц, а для второй =12 кГц.

Рисунок 4.10  Примеры спектров отраженных сигналов для режима СЧП для двух ЧПИ, равных =15 кГц и =18 кГц

На рисунке 4.10,г показана зависимость изменение наблюдаемых доплеровских частот целей при расположении зоны фильтрации “правее” основной составляющей МО по ГЛ при , а на рисунке 4.10,д - при . В рассматриваемом случае уравнения, аналогичные (4.56), необходимо записать по другому (как это следует из рисунка 4.10, г и рисунка 4.10, д):

(4.57)

где m и n могут быть положительными и отрицательными целыми числами. Для рассматриваемого примера для первой цели m=1, n=1, а для второй цели m=-2, n=-2.

Определить истинное значение доплеровской частоты цели по уравнениям (4.57) можно методом перебора величин m и n. Совпадение значений при вычислении по формулам (4.57), в случае перебора величин тип, возможно только при определенных значениях m и n.

Действительно, в рассматриваемом на рисунке 4.10 примере можно для двух наблюдаемых допплеровских частот при каждой ЧПИ выполнить вычисления с перебором величин m и n по формуле (4.57) и составить расчетную таблицу 4.5, в которой приведены вычисленные значения для .

Таблица 4.5  Вычисленные значения для

m или n		-3	-2	-1	0	+1	+2	+3
		…	15	30	45	60	75	…
		…	12	27	42	57	72	…
		…	6	24	42	60	78	…
		…	12	30	48	66	84	…

Выводы: Из таблицы 4.5 видно, что для одной цели, имеющей и , совпадение , вычисленных по (4.57) при различных m и n, соответствует частоте 60 кГц. Это и есть допплеровская частота первой цели = 60 кГц. Аналогично, для другой цели, имеющей = 6 кГц и = 12кГц, совпадение , вычисленных при различных тип, соответствует частоте 12 кГц. Это допплеровская частота второй цели = 12 кГц, которая находится на догонном курсе.

В реальных ИДР в общем случае требуется больше ЧПИ, чем две, так как возможны случайные попадания наблюдаемой частотной составляющей цели в «слепую» зону при изменении частоты повторения импульсов. В этом случае потребуется применить третью ЧПИ для устранения влияния «слепой» зоны и вычислить однозначное значение истинной доплеровской частоты.

В современных ИДР как «дальномерные», так и «доплеровские» ЧПИ объединяются и при этом одновременно устраняются «слепые» зоны и вычисляются однозначные значения дальностей и допплеровских частот. Обычно требуется значительно больше ЧПИ, чем 2-3. Известны варианты построения ИДР, в которых применяются наборы ЧПИ от шести до десяти ЧПИ за время облучения цели, а в ряде случаев и больше.