2 Основные принципы функционирования следящих каналов дальности, скорости и угловых координат

2.1 Обеспечение необходимой точности захвата целей на сопровождение по дальности

Поскольку точность измерения дальности до цели на этапе об­зора в режиме ВЧП недостаточная для ввода канала дальности в ре­жим сопровождения, необходимо уменьшить ошибки ее измерения. Для этих целей можно использовать так называемый нониусный ме­тод. Суть данного метода состоит в следующем.

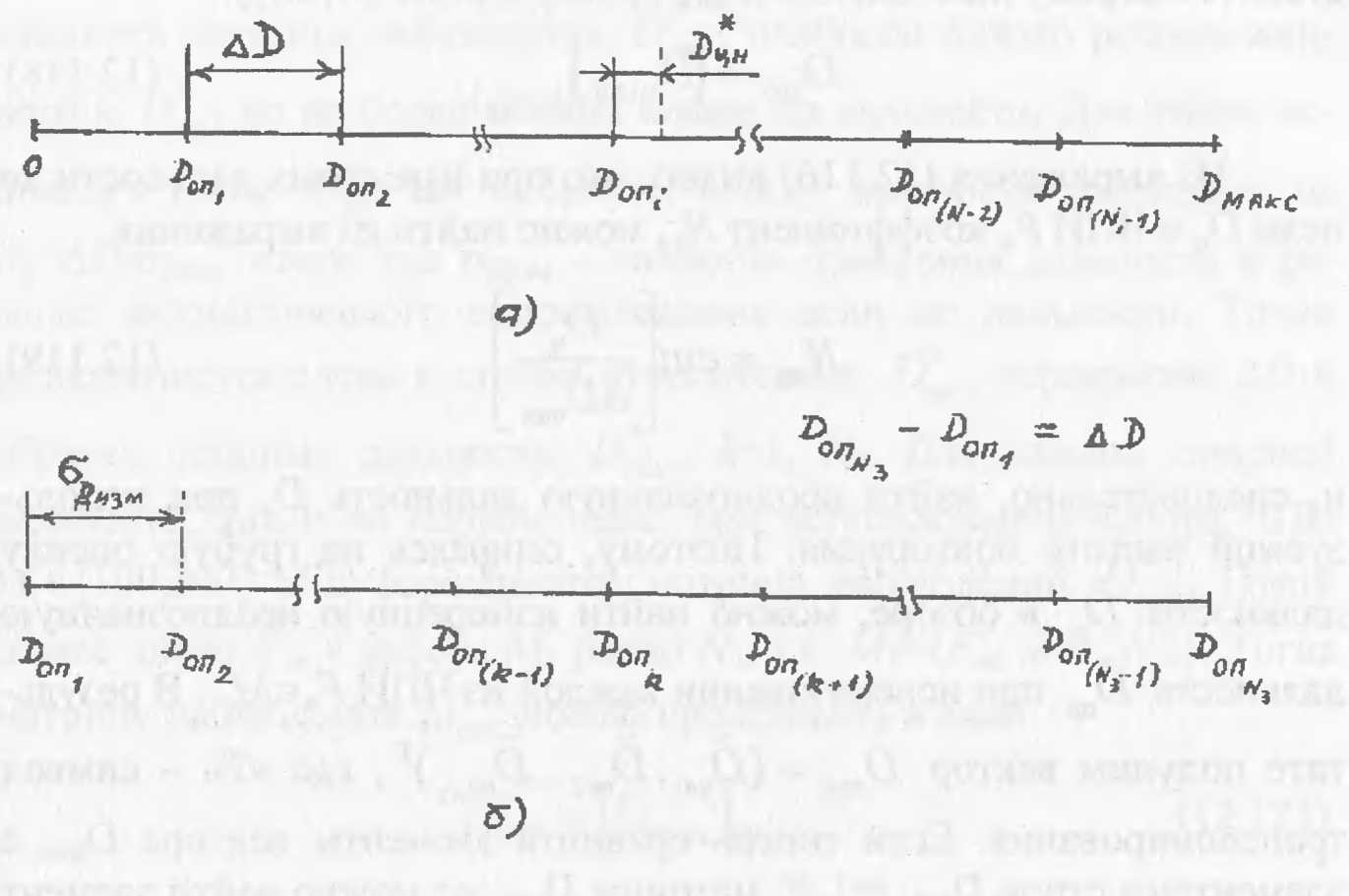
Рисунок. 2.1˗˗Временные диаграммы синусного метода измерения дальности

Известно, что в режиме ВЧП дальность до цели D_ц измеряется неоднозначно. Величину D_цможно представить в виде

D_ц =N_кр∆D_одн + D_и (2.1)

где N_кр - кратность неоднозначности, определенная ранее; ∆D_одн=0,5сt_и - интервал однозначного измерения дальности, D_и=0,5сt_Dн - наблюдаемая дальность.

Разобьем весь диапазон от нулевой до максимальной дальности обнаружения D_макс цели ИД РЛС на участки равной протяженности ∆D по дальности (риске 2.1). Величина ∆D, как правило, выбирается не больше среднеквадратической ошибки σ_Добн измерения дальности в режиме обзора, т.е. σ_Добн>∆D.

Возьмем фиксированный набор частот повторения импульсов М_о из диапазона 100...200 кГц (диапазон ЧПИ при ВЧП). Для каждой опорной дальности D_опт=i∆D, i [1, N₁], где N₁ = D_макс/∆D, и для каждой частоты повторения F_иj   M_o вычислим неоднозначные дальности наблюдения (опорные неоднозначные дальности) D_{оп нij} с учетом (2.1) по правилу

(2.2)

где , , – кратность неоднозначности, интервал однозначности и неоднозначная дальность для 1-й опорной дальности и j – й ЧПИ набора М_o,;

ent[.] - целая часть числа.

Пусть общее число ЧПИ в наборе равно N₂. Тогда можно составить матрицу наблюдений Д_наб, размерностью (N₁xN₂):

Из выражения (2.1) видно, что при известных дальности до цели D_ц и ЧПИ F_и коэффициент N_кр можно найти из выражения

(2.3)

и, следовательно, найти неоднозначную дальность D_н при используемой частоте повторения. Поэтому, опираясь на грубую оценку дальности в обзоре, можно найти измеренную неоднозначную дальность при использовании каждой из ЧПИ F_n  M_o . В результате получим вектор D_изм = ( , … )^Т где «T» - символтранспонирования. Если теперь сравнить элементы вектора D_изм с элементами строк D_опi, i=1, N₁ матрицы D_наб, то можно найти элемент D_опij, который по своему значению близок к значению одного из элементов вектора D_изм. Это позволит в соответствии с (2.1) определить истинную дальность до цели. Если бы цель была неподвижна, то совпадение значений D_опij и было бы полным. Поэтому необходимо уточнить значение D_опij, что можно сделать, например, повторив операцию сравнения элементов вектора D_изм и строк матрицы D_наб при использовании ЧПИ F_иj   M_o, но при их следовании в обратном направлении, от большего номера ЧПИ к меньшему. Обозначим выбранный элемент матрицы D_наб при использовании набора F_иj, i=1, N₀ при изменении номера у от 1 до N₂, как , ав случае изменения номера ЧПИ от N₂ к 1, как . Тогда значение неоднозначной опорной дальности будет равно

(2.4)

Данное значение используется для повышения точности измерения D_ц на втором этапе (см. рисунке. 2.1, 6), который состоит в поиске элемента матрицы наблюдения , наиболее близко расположенного к , но на более мелкой шкале по дальности. Для этого, используя точку как опорную, шкалу дальности разбивают на точек, где - точность измерения дальности в режиме автоматического сопровождения цели по дальности. Точки располагаются слева и справа относительно , перекрывая ∆D и образуя опорные дальности , k= 1, N₃. Для каждой опорной дальности, как и на первом шаге, при использовании набора ЧПИ М₁   [100,200]  кГц формируется матрица наблюдений . Пусть общее число F_иe в наборе М₁ равно N₄, т.е. М₁ ={F_иe,e = 1, N₄}. Тогда матрицу наблюдения можно представить в виде

(2.5)

Элементы строк матрицы сравниваются с вектором измерений , который формируется аналогично вектору для частот повторения из набора М₁ при использовании в качестве измеренного значения дальности величины ;. где , и – частоты повторений, при которых получены и соответственно, входящие в выражение (2.4). Набор частот повторений M₁, как и на первом шаге используется дважды. Первоначально при изменении номера ЧПИ от 1 до N₄, а затем - от N₄ до 1.

В результате сравнения элементов матрицы и вектора измерений находятся неоднозначные дальности при использовании набора М_1. В результате вычисляются дальности до цели

где индексы 1 и 2 соответствуют использованию набора М₁ при увеличении номера l с 1 до N₄ и уменьшении l с N₄ до 1 соответственно.

Результаты измерений и сравниваются. Если модуль разности удовлетворяет условию

(2.6)

где – протяженность строба захвата по дальности, то полагают и осуществляется переход ИДР в режим автоматического сопровождения цели по дальности. В противном случае вычисление продолжается.