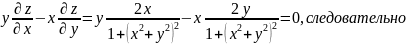Tipovoy_raschet_variant_15_ryady_bntu

Контрольная работа №10.

Вариант 15.

Задание 1. Исследовать данные ряды на сходимость:

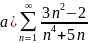
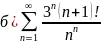
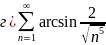
Решение:

а)

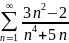
Воспользуемся признаком сравнения в предельной форме:

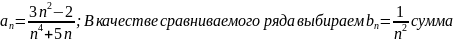
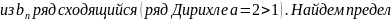
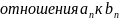
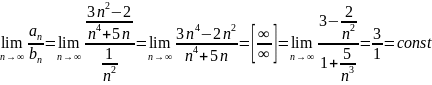
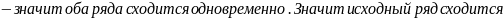
Воспользуемся признаком Даламбера. Здесь

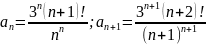
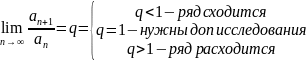
Вычислим предел:

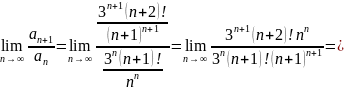
Согласно признака Даламбера ряд расходится.

Для ответа на вопрос о сходимости ряда применим радикальный признак Коши

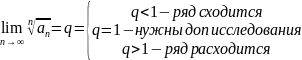
Вычислим предел:

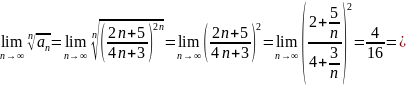
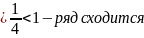
Воспользуемся признаком сравнения в предельной форме:

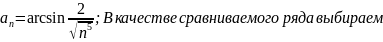
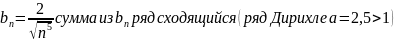
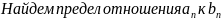
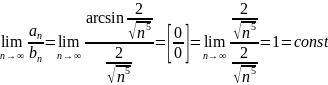
Ответ: а) ряд сходится; б)ряд расходится; в) ряд сходится; г) ряд сходится;

Задание 2. Найти область сходимости ряда:

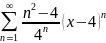
Решение: Воспользуемся признаком Даламбера

Выпишем

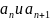
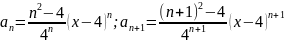
Воспользуемся признаком Д’Aламбера:

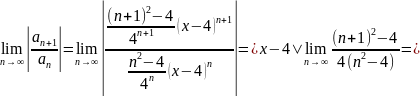
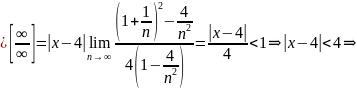
Исследуем данный ряд на концах интервала сходимости:

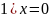
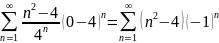
Применим признак Лейбница:

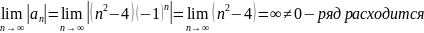
Проверим необходимое условие сходимости:

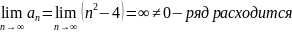
Областью сходимости является

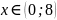
Ответ: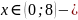 область сходимости

Задание 3. Вычислить определенный интеграл с точностью до 0,001, разложив подынтегральную функцию в ряд и затем проинтегрировав его почленно:

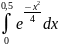
Решение: запишем разложение

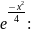
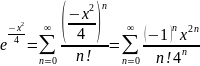
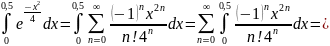
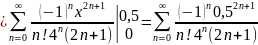
Для получения заданной точности нужно первые три члена, поскольку

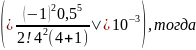
Ответ: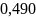

Задание 4. Найти три первых отличных от нуля члена разложения в степенной ряд решения дифференциального уравнения, удовлетворяющего заданному начальному условию:

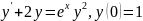
Решение:

Для представления решения в виде ряда Маклорена необходимо найти первые три отличные от нуля значения 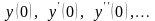. По условию задачи y(0)=0 Выразим из уравнения :

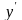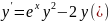
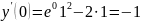
Найдем 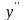, продифференцировав обе части равенства 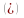по :

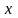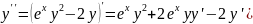
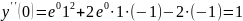
Окончательно получим:

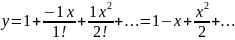
Ответ:

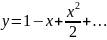
Задание 5. Разложить функцию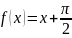 в ряд Фурье по косинусам в интервале ( ; )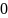

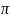Решение: Ряд Фурье будет по косинусам функции f(x) периода T=2 , непрерывной или имеющей конечное число точек разрывов первого рода отрезке (0; ), имеет вид:

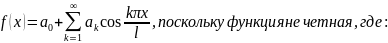
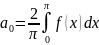
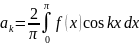
Вычисляем коэффициенты:

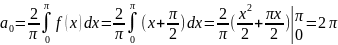
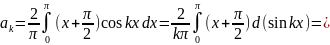
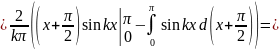
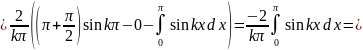
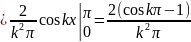
Тогда разложение имеет вид:

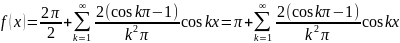
Ответ:

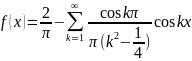
Задание 6. Определить, является ли функция 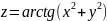решением дифференциального уравнения в частных производных

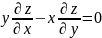
Решение:

Вычислим частные производные по х и по у:

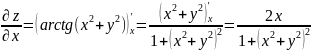
Подставим данные значения в дифференциальное равенство: