
- •Аннотация
- •Содержание
- •Введение
- •1. Анализ цепи во временной области методом переменных состояния при постоянных воздействиях
- •Анализ цепи операторным методом при апериодическом воздействии
- •3. Качественный анализ цепи частотным методом при апериодическом воздействии.
- •4. Анализ цепи частотным методом при периодическом воздействии
- •Список использованных источников
МИНОБРНАУКИ
РОССИИ
Федеральное
государственное автономное образовательное
учреждение высшего образования Санкт-Петербургский
государственный электротехнический
университет “ЛЭТИ” им. В. И. Ульянова
(Ленина) (СПбГЭТУ «ЛЭТИ»)




Кафедра теоретических основ электротехники
КУРСОВАЯ РАБОТА
по дисциплине «ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ЭЛЕКТРОТЕХНИКИ»
Тема № 3: «ИССЛЕДОВАНИЕ ЛИНЕЙНОЙ ЦЕПИ В ПЕРЕХОДНЫХ И УСТАНОВИВШЕМСЯ ПЕРИОДИЧЕСКОМ РЕЖИМАХ»
Вариант № 1
Студент гр. |
|
|
Преподаватель |
|
Сердюк А.П. |
Санкт-Петербург
2024 г.
ЗАДАНИЕ
на курсовую работу
Студент: |
||
Группа |
||
Тема работы: Исследование линейной цепи в переходных и установившемся периодическом режимах
|
||
Исходные данные: Дана электрическая цепь:
Rн = 103 Ом, R1 = 0,5 ∙ 103 Ом, R3 = 2 · 103 Ом, С = 0,033 ∙ 10–6 Ф, L = 0,03 Гн, U0 = 6 В, I0 = 4 ∙ 10-3 А, i0(t) = 4 ∙ 10-3𝛿1(𝑡), Um = 10 В, u0(t) = const = 6 В, tи = 6 ∙ 10-5 с, Т = 12 ∙ 10-5 с Одиночный импульс:
|
||
Содержание пояснительной записки: Аннотация, Содержание, Введение, Заключение, Список использованных источников |
||
Предполагаемый объем пояснительной записки: Не менее 25 страниц |
||
Дата выдачи задания: 05.02.2023 г. |
||
Дата сдачи курсовой работы: . .2023 г. |
||
Дата защиты курсовой работы: . .2023 г. |
||
Студент |
|
|
Преподаватель |
|
Сердюк А.П. |
Аннотация
В данной работе была рассмотрена электрическая цепь второго порядка: установлены собственные частоты цепи двумя способами (через формирование системы уравнений состояния и операторным методом через определение передаточной функции цепи), а также рассматривались выходные сигналы при одиночном импульсе.
Summary
In this paper, the second-order electrical circuit was considered: the eigenfrequencies of the circuit were established in two ways (through the formation of a system of equations of state and by the operator method through the determination of the transmission function of the circuit), and the output signals were considered for a single pulse.
Содержание
|
Введение |
7 |
1. |
|
8 |
1.1. |
Составление уравнений состояния цепи для t ≥ 0 |
8 |
1.2. 1.3.
|
Нахождение аналитических решений уравнений состояния Нахождение решения уравнений состояния, используя метод Эйлера |
10 11 |
2. |
Анализ цепи операторным методом при апериодическом воздействии |
14 |
2.1. |
Определение передаточной функции |
14 |
2.2. 2.3.
2.4.
2.5.
2.6. |
Определение нулей и полюсов передаточной функции Определение переходной (h1(t)) и импульсной (h(t)) характеристик для выходного сигнала Определение изображения по Лапласу входного одиночного импульса Определение напряжения Uн (t) на выходе цепи, используя передаточную функцию Построение графиков переходной и импульсных характеристик цепи, а также входного и выходного сигналов |
15
15
16
17
17 |
3. |
Качественный анализ цепи частотным методом при апериодическом воздействии. |
19 |
3.1.
|
Нахождение и построение АФХ, АЧХ и ФЧХ функции передачи цепи |
19 |
3.2. 3.3.
3.4. 4.
4.1.
4.2.
4.3.
|
Определение
полосы пропускания цепи по уровню
Нахождение
и построение амплитудного и фазового
спектров апериодического входного
сигнала и определение ширины спектра
по уровню
Заключение об ожидаемых искажениях сигнала на выходе цепи
Построить
графики входного периодического
сигнала/его аппроксимации (рис. 4.6) и
напряжения
|
22
22 23
24
24
24
26 |


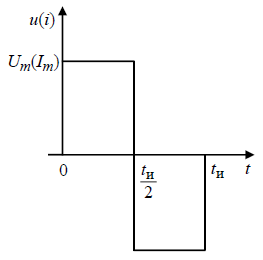
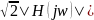
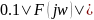
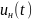 на выходе цепи в виде отрезка Фурье
и построить амплитудный и фазовый
спектры выходного сигнала
на выходе цепи в виде отрезка Фурье
и построить амплитудный и фазовый
спектры выходного сигнала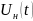 на выходе в виде суммы гармоник (рис.
4.7).
на выходе в виде суммы гармоник (рис.
4.7).