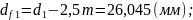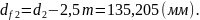21-ЭУД Белецкая 9 вариант / ДМ работа #2

Проектировочного расчёта цилиндрической зубчатой передачи.

Исходные данные – из энергетического и кинематического расчётов:

Момент на шестерне z₁: T₁=27,04 Н⋅м;

частота вращения z₁: n₁=1440мин^-1;

передаточное число: u=4,5;

ресурс: h=4 года, k_г=0,8; k_с=0,66.

На рисунке представлена кинематическая схема проектируемого одноступенчатого зубчатого редуктора. Начиная с этой задачи, обозначения параметров будут соответствовать данной схеме.

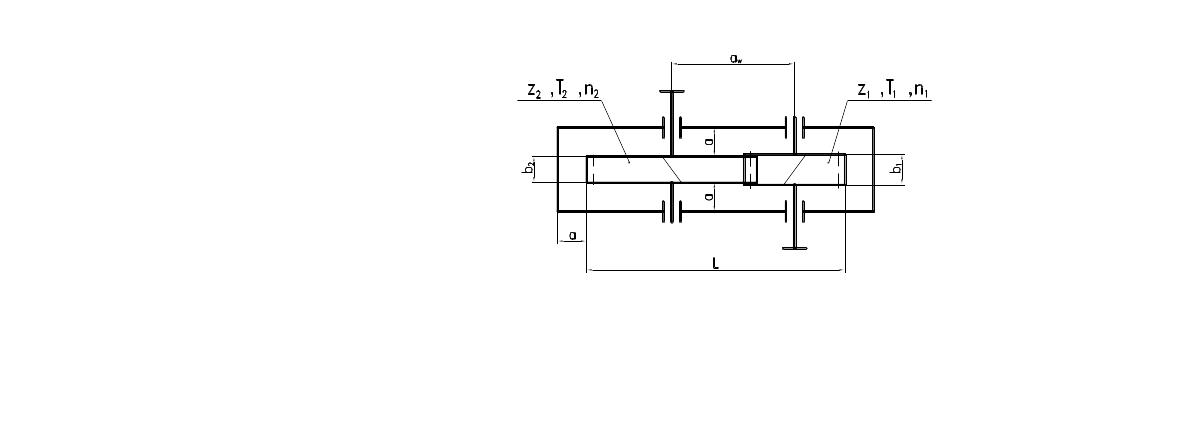
Нагрузка на зубья переменная, напряжения изменяются по отнулевому циклу (коэффициент асимметрии цикла R=0). Передача закрытая, основной вид разрушения зубьев – усталостное выкрашивание активных поверхностей зубьев под действием контактных напряжений 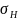_.Проектировочный расчет цилиндрической зубчатой передачи начинается с определения межосевого расстояния а_w из условия сопротивления контактной усталости зубьев с последующими проверками величин контактных напряжений и напряжений изгиба σ_F.

1. Материал и термообработка.

В нашей задаче принимаем материал для шестерни и колеса – сталь 40Х ГОСТ4543-71, тогда по таблице 1.1 [2]:

а) шестерня, z₁: термообработка - закалка ТВЧ; σ_в =900 МПа, σ_Т=750 МПа, твёрдость зубьев по Роквеллу 45…50 HRC (425…480 HB).

Средняя твёрдость зубьев z₁ : 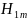=452 HB;

б) колесо z₂: термообработка – улучшение, твёрдость 269…302 HB.

Средняя твёрдость зубьев z₂ : 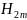=285 HB. - =167 >100 HB - рекомендация по перепаду твёрдостей зубьев выполняется.

2. Число циклов перемены напряжений

Срок службы (ресурс) передачи:

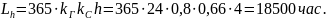
Суммарное число циклов перемены напряжений за весь срок службы:

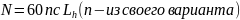
• для шестерни: N₁=60⋅…⋅1⋅18500=…10⁷;

• для колеса: N₂= N₁/ u= …/4,5=…⋅10⁷.

Базовое число циклов по контактным напряжениям:

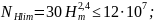
- по напряжениям изгиба: .

По таблице 2.2 [2]:

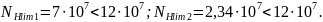
Из сравнения чисел циклов имеем, что N₁ и N₂> N_Hlim; N₁ и N₂> N_Flim. Отсюда коэффициенты долговечности Z_N =1; Y_N =1.

3. Допускаемые напряжения.

Для косозубых и шевронных цилиндрических передач по формуле 3.4 [2]:

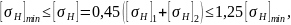
где

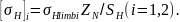
Базовый предел контактной выносливости при N_Hlim по таблице 3.1 [2]:

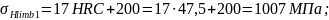
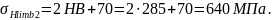
Коэффициент запаса прочности: S_H1=1,2; S_H2=1,1. Тогда получаем:

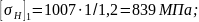
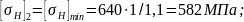
582 <0,45 (839+582) =639 <1,25⋅582=728 МПа. Граничные условия формулы 3.4 выполняются.

Расчетное контактное допускаемое напряжение

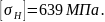
4. Предварительное значение межосевого расстояния :

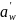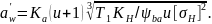
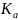=410 – вспомогательный коэффициент для косозубых передач.

Принимаем 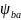=0,4 – для симметричного расположения колёс относительно опор.

Определим коэффициент нагрузки в расчётах на контактную прочность .

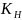Окружная скорость:

Рекомендуемая степень точности по таблице 4.3 [2]: n_ст=8. Далее по таблице 4.4 [2] (v=… м/с, n_ст=8, H₁>350HB, H₂<350HB, зубья косые) получим коэффициент динамической нагрузки .

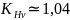Коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий из-за погрешностей изготовления и упругих деформаций детали:

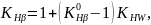
где – коэффициент неравномерности распределения нагрузки в начальный период до приработки зубьев. Для одноступенчатых цилиндрических зубчатых редукторов находится по таблице 2.7 [3], в зависимости от 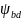и твёрдости зубьев.

Таблица 2.7 [3]

		Значения KHβ0 при коэффициенте ψbd
		0,4	0,6	0,8	1,0	1,2	1,4	1,6
Твердость зубьев	≤350 HB	1,02	1,03	1,03	1,04	1,06	1,08	1,11
	>350 HB	1,02	1,05	1,07	1,11	1,15	1,20	1,26

Таблица 2.8 [3]

Твердость поверхности зубьев	Значения KHw при скорости v, м/с
	1	3	5	8	10	15
200 HB	0,19	0,20	0,22	0,27	0,32	0,54
250 HB	0,26	0,28	0,32	0,39	0,45	0,67
300 HB	0,35	0,37	0,41	0,50	0,58	0,87
350 HB	0,45	0,46	0,53	0,64	0,73	1,00
43 HRC	0,53	0,57	0,63	0,78	0,91	1,00
47 HRC	0,63	0,70	0,78	0,98	1,00	1,00
51 HRC	0,71	0,90	1,00	1,00	1,00	1,00
60 HRC	0,80	0,90	1,00	1,00	1,00	1,00

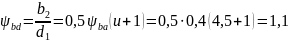
При H₂<350 HB интерполяцией находим :

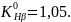
Коэффициент 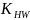определяется по таблице 2.8 [3], при v ≃… м/с, и H₂=285HB получаем: 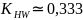отсюда:

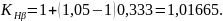
Коэффициент неравномерности распределения нагрузки между парами зубьев:

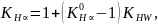
где 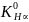– начальное значение до приработки в зависимости от степени точности n_ст:

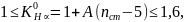
где A=0,25 при H2≤350 HB. Тогда получаем:

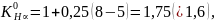
то есть следует принять степень точности n_ст=7 (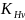 при этом не меняется), тогда:

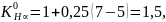
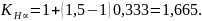
Коэффициент расчётной нагрузки по контактным напряжениям:

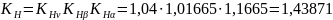
Расчётное контактное допускаемое напряжение принимаем

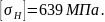
Определяем межосевое расстояние:

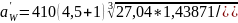
Округляя в большую сторону до ближайшего стандартного значения получаем a_W=85 мм.

5. Ширина зубчатого венца.

Ширина венца колеса:

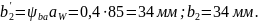
Ширина венца шестерни:

b₁ = b₂ + (3…5) мм; принимаем b₁ =38 мм.

6. Модуль передачи.

Максимально допустимый, из условия неподрезания зубьев у основания [3]:

Принимаем m=1,75 мм.

Расчётное значение округляется по ГОСТ 9563-60 (см. [2], стр. 20).

7. Угол наклона зубьев.

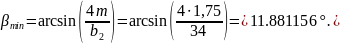
8. Суммарное число зубьев.

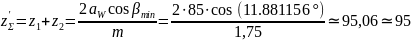
Далее уточняем значение β (с точностью до 10^-6):

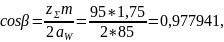
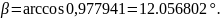
Для косозубых передач рекомендовано β = (8…20) ⁰.

9. Числа зубьев z₁ и z₂.

Число зубьев шестерни:

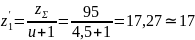
Из условия отсутствия подрезания:

.

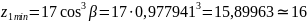Принимаем z₁=17.

Число зубьев колеса:

10. Фактическое передаточное число редуктора.

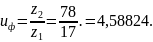
Его следует использовать в дальнейших расчётах. Оно должно отличаться от номинального (u_ред=4,5) для одноступенчатого редуктора в пределах ±3%.

11. Диаметры зубчатых колёс: (с точностью до сотых)

- делительные

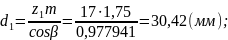
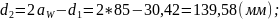
- окружностей вершин:

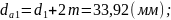
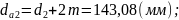
- окружностей впадин: