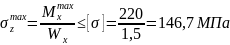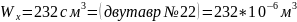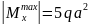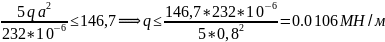ЭУД сопромат 2 семестр 10 вар / Схема 43+

Схема №43

1.6 Расчёт на прочность и жёсткость статически неопределимых элементов конструкций при изгибе.

1.6.1 Условие задачи

q= 0,014 МН/м, а = 0,8 м, p = qa, m = 3qa²;

Для стальной (Ст3) балки (схема 43), выполненной из двутавра №10, из условия прочности определить допустимую нагрузку. 1.6.2 Краткие теоретические сведения.

Система канонических уравнений метода сил:

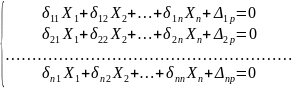(1)

Где 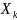– реакция k-ой связи;

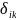
­ – единичное перемещение по направлению i-ой связи, вызванное реакцией ;

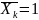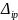– перемещение по направлению i-ой связи, вызванное одновременным действием всей внешней нагрузки.

Количество слагаемых в каждом из уравнений (1) и их общее число, определяется степенью статической неопределимости системы. Коэффициенты системы канонических уравнений (1) определяются методом Мора-Верещагина путем перемножения соответствующих эпюр.

Условие прочности на изгиб имеет вид:

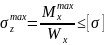(2)

Где 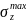– максимальное нормальное напряжение, МПа;

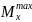– Максимальный изгибающий момент, МН*м;

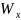– Осевой момент сопротивления;

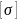– допустимое нормальное напряжение, МПа;

1.6.3 Решение задачи.

1) Определяем степень статической неопределимости:

n = 4-3 = 1

2) Выбираем ОС (основную систему)

3) Приводим ОС к ЭС (эквивалентной системе)

4) Составим уравнение эквивалентности в каноническом виде:

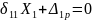
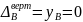(Перемещение в точке В = 0)

5) Найдём коэффициенты канонического уравнения

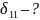
Строим эпюру 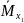, от первого ЕС (единичного состояния)

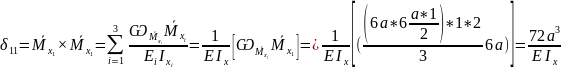
Находим коэффициент

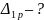
Строим эпюру 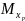от системы с внешними нагрузками.

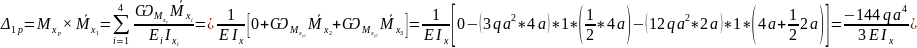
6) Окончательная эквивалентная система (О.Э.С.)

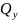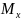Покажем окончательную эквивалентную систему(ОЭС). Строим и под окончательной эквивалентной системой.

7) Деформационная проверка.

7.1) Задаём НОС (новую основную систему)

Определим угол поворота в опоре А, который должен равняться нулю как в заданной системе.

Задаём 2ЕС.

Строим эпюру 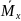от 2-го единичного состояния.

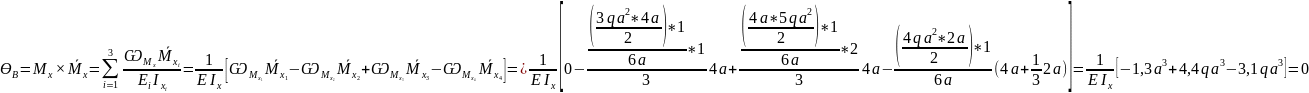
7) Из условий прочности определим дополнительную нагрузку q для стальной балки, выполненной из двутавра №22