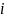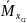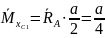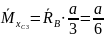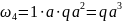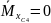Схема
35
Схема
35
Для
двухопорной балки постоянной жёсткости
 в общем виде определить методом Мора
прогиб в сечении С,
в общем виде определить методом Мора
прогиб в сечении С,
способом Верещагина прогибы в сечениях C и D и угол поворота на правой опоре. Используя вид эпюры и
вычисленные значения прогибов и угла поворота, показать характер изогнутой оси балки.
Дано:
q=
0,014 МН/м, а = 0,8 м, P
= qa,
m
=
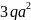 ,
𝜎𝑇=220
МПа ; nв=1.5,
,
𝜎𝑇=220
МПа ; nв=1.5,
Е=0.71*10^5МПа; ,
1. Определим перемещение точки С по формуле Мора.
1.1. Задаём единичное состояние.
1.2. Определяем реакции опор.
Грузовое
состояние (ГС): реакции найдены эскизно.

Проверка:

Первое единичное состояние (1ЕС): реакции найдены эскизно
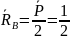
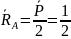
Второе единичное состояние (2ЕС): реакции найдены эскизно
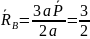

Третье единичное состояние (3ЕС): реакции найдены эскизно


1.3. Записываем аналитические выражения изгибающих моментов на каждом силовом участке.
I
участок

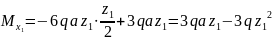



II
участок





III
участок
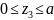



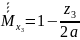
Определяем прогиб сечения С по формуле Мора.



Сечение C перемещается вниз.
2. Определим прогиб сечений С, D и угол поворота на опоре B способом Верещагина.
2.1.
Строим эпюры
 и
и

2.2.
Разбиваем грузовую эпюру на простые
элементы
 и определяем соответствующие им ординаты
и определяем соответствующие им ординаты
единичных эпюр.
 Результаты
заносим в таблицу.
Результаты
заносим в таблицу.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.3. Вычисляем:


Сечение D перемещается вверх.

Поворот сечения B происходит против часовой стрелки.
3. Показываем примерный характер изогнутой оси балки.
4. Условие прочности при изгибе:



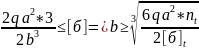
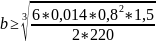
 0,057
м.; b=0,057
м.
0,057
м.; b=0,057
м.
5. Условие
жёсткости при изгибе:
Условие
жёсткости при изгибе:
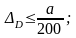
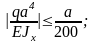

6. Сравнивая результаты расчетов на прочность и жесткость, выбираем больший из полученных размеров, как удовлетворяющий обоим условиям: b=0,0741 м.