Voprosy_po_optimizatsii (2)

Вопросы к экзамену по методам оптимизации 2013

1. Унимодальность, выпуклость и вогнутость функции. Пример.

2. Необходимые и достаточные условия существования экстремума функции нескольких переменных.

3. Сокращение интервала неопределенности.

4. Метод дихотомии. Пример реализации одного шага в электронных таблицах (Excel/Calc).

5. Метод Фибоначчи.

6. Метод золотого сечения. Пример реализации одного шага в электронных таблицах (Excel/Calc).

7. Методы прямого поиска. Покоординатный спуск. Пример вычисления шага по одной переменной в электронных таблицах (Excel/Calc).

8. Покоординатный спуск. Пример реализации одного шага в MathCAD.

9. Метод Хука-Дживса. Пример реализации одного шага в MathCAD.

10. Метод деформируемого многогранника (Нелдера-Мида).

11. Градиентные методы. Наискорейший спуск. Пример реализации одного шага в электронных таблицах (Excel/Calc).

12. Градиентные методы. Наискорейший спуск. Пример реализации одного шага в MathCAD.

13. Методы второго порядка. Метод Ньютона. Пример реализации одного шага в электронных таблицах (Excel/Calc).

14. Методы второго порядка. Метод Ньютона. Пример реализации одного шага в MathCAD.

15. Задача нелинейного программирования с ограничениями в виде равенства. Функция Лагранжа. Множители Лагранжа. Пример реализации одного шага в MathCAD.

16. Штрафные функции. Решение задачи нелинейного программирования с ограничениями в виде равенств. Пример записи штрафной функции в MathCAD.

17. Барьерные функции. Решение задачи нелинейного программирования с ограничениями в виде неравенств. Пример записи барьерной функции в MathCAD.

18. Постановка задачи линейного программирования. Задача о рациональном распределении ресурсов. Каноническая и стандартная форма задачи ЛП.

19. Симплекс-метод для решения задачи ЛП.

20. Решение задачи ЛП в электронных таблицах (Excel/Calc).

21. Постановка транспортной задачи. Метод потенциалов для решения транспортной задачи.

22. Решение транспортной задачи в электронных таблицах (Excel/Calc).

23. Многокритериальная оптимизация. Оптимальность по Парето. Основные определения.

24. Метод свертки критериев для решения задач многокритериальной оптимизации. Пример реализации одного шага в MathCAD.

25. Дискриминационный метод для решения задач многокритериальной оптимизации. Пример реализации одного шага в MathCAD.

26. Метод последовательных уступок для решения задач многокритериальной оптимизации. Пример реализации одного шага в MathCAD.

27. Метод имитации отжига для решения задач глобальной оптимизации. Алгоритм метода. Методы «тушения».

5. Экстремум функции нескольких переменных. Необходимые и достаточные условия существования экстремума

Определение 7. Точка  называется точкой минимума (максимума) функции , если существует такая окрестность точки , что для всех точек  из этой окрестности выполняется неравенство , ().

Точки минимума и максимума функции  называются точками экстремума, а значения функции в этих точках – экстремумами функции (минимумом и максимумом соответственно).

Заметим, что минимум и максимум функции имеют локальный характер, так как значение функции в точке  сравнивается с ее значениями в точках, достаточно близких к .

Теорема 1 (необходимые условия экстремума). Если  – точка экстремума дифференцируемой функции , то ее частные производные  и  в этой точке равны нулю:  .

Точки, в которых частные производные первого порядка равны нулю, называются критическими или стационарными. В критических точках функция  может иметь экстремум, а может и не иметь.

Теорема 2 (достаточное условие экстремума). Пусть функция : а) определена в некоторой окрестности критической точки , в которой  и ; б) имеет непрерывные частные производные второго порядка   . Тогда, если , то функция  в точке  имеет экстремум: максимум, если А<0; минимум, если А>0; если , то функция  в точке  экстремума не имеет. В случае  вопрос о наличии экстремума остается открытым.

При исследовании функции двух переменных на экстремум рекомендуется использовать следующую схему:

1.         Найти частные производные первого порядка:  и .

2.         Решить систему уравнен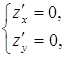ий  и найти критические точки функции.

3.         Найти частные производные второго порядка: , , .

4.         Вычислить значения частных производных второго порядка в каждой критической точке и, используя достаточные условия, сделать вывод о наличии экстремума.

5.         Найти экстремумы функции.