3. Порядок выполнениия работы.

• Нагружать образец вращением штурвала винта передачи винт-гайка 3 последовательно силой 500 Н, 1000 Н, 1500 Н. Растягивающую силу устанавливать по показаниям индикатора 6. Т. е. нагрузку увеличивать равными ступенями. Для каждой ступени кН.

• Фиксировать показания ИД для каждого тензорезистора на каждом уровне силы. Для перехода от замеряемой ИД электрической величины к механической деформации образца использовать тарировочный коэффициент, устанавливающий соответствие между данными величинами.

• Определить приращение продольной и поперечной деформаций образца, соответствующие приращению силыпо формулам:

где – цена единицы дискретности ИД (тарировочный

коэффициент).

• Вычислить модуль продольной упругости материала по формуле:

где – продольная деформация, – нормальное напряжение, Н/мм².

Определить коэффициент поперечной деформации (коэффициент Пуассона) по формуле:

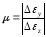
где – поперечная деформация, – продольная деформация.

4.Результаты эксперимента

Размеры образца h =2,5 мм , b = 30мм, A = hb мм².

Тарировочный коэффициент =10^-6.

Пока-зания инди-като-ра

Нагрузка

Показания измерителя деформаций

F, Н

∆F, Н

A Продольный

B (2) поперечный

C (3) поперечный

D (4) продольный

nf

nz

∆nz

ny

∆ny

ny׳

∆ny׳

nz׳

∆nz׳

0

0

500

106

500

500

212

1000

500

318

1500

Средние значения

∆F ср

∆nz ср

∆ny ср

∆ny׳ср

∆nz׳ср

500

Приращение продольной деформации

_{Приращение поперечной деформации}

Приращение нормального напряжения (МПа)

Модуль продольной упругости (модуль Юнга) (МПа)

Коэффициент Пуассона (поперечной деформации)

Полученные значения модуля упругости Е и коэффициента Пуассона μ необходимо сравнить с табличными данными:

– для стали Е = (1,9…2,1)•10⁵ МПа, μ = 0,25 … 0,3

– для алюминия Е = 0.,69•10⁵ МПа, μ = 0,32 … 0,36

Лабораторная работа № 2 Определение нормальных напряжений в сечениях балки при прямом изгибе

Цель работы. Проверка закона распределения нормальных напряжений в поперечном сечении балки при прямом изгибе.

1.Краткие теоретические сведения.

Нормальные напряжения при прямом изгибе определяются по формуле:

,

где – изгибающий момент в рассматриваемом поперечном сечении балки относительно нейтральной оси (оси Х);

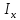–осевой момент инерции поперечного сечения относительно

той же оси Х;

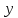- расстояние от оси Х до точки сечения, где определяются

напряжения.

Из приведенной формулы видно, что распределение нормальных напряжений по высоте сечения носит линейный характер (–в первой степени). Максимального значения напряжения достигают в точках, наиболее удаленных от нейтральной оси, т.е. при отрицательных и положительных значениях.

При выводе формулы приняты гипотезы:

• плоских сечений;

• о ненадавливании продольных волокон, т. е. .

Напряжения в растянутой зоне балки при чистом изгибе являются главными напряжениямиσ_1, в сжатой зоне – σ_{3 ,} а площадки, на которых они действуют, – главными площадками, совпадающими с поперечным сечением балки.

Для проверки закона распределения нормальных напряжений в поперечном сечении балки при прямом изгибе необходимо экспериментально определить напряжения в различных точках сечения.

С этой целью измеряют деформацию в различных точках

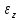поперечного сечения балки с помощью тензорезисторов. Затем расчитывают нормальные напряжения в данных точках, умножая экспериментально полученную деформацию растяжения или сжатия на модуль продольной упругости :.