5.Экспериментальное определение напряжений в опасной точке сечения а и угла поворота главных площадок

Нагрузка F (H)	Т.Р. № 1		Т.Р. № 2		Т.Р. № 3
	ось Z		oсь V		oсь U
	n Z	∆ nZ	nV	∆ nV	nU	∆ nU
0
20
40
60
∆ n ср

Линейная деформация на ступень нагружения

,

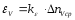
Главные напряжения на ступень нагружения

,

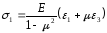7. Сопоставление результатов расчета и эксперимента

Параметр
Теоретический расчет
Эксперимент
Погрешность %

Лабораторная работа № 6

Определение критической силы при продольном сжатии стержня большой гибкости

Цель работы. Демонстрация явления потери устойчивости формы стержня в упругой стадии. Определение величины критической силы при продольном изгибе стержня и сопоставление установленной опытным путем величины критической силы с ее значением, рассчитанным по соответствующим формулам сопротивления материалов.

1.Краткие теоретические сведения.

При нагружении прямолинейного закрепленного по концам стального стержня продольной центрально приложенной нагрузкой, стержень до некоторых пор сохраняет свою первоначальную форму, а затем при достижении силой некоторого значения Р_кр выпучивается (искривляется). Нагрузка, при которой наряду с первоначальной прямолинейной равновесной формой стержня возможна новая искривленная равновесная форма, бесконечно близкая к прямолинейной, называется критической. При незначительном увеличении нагрузки больше критической происходят значительные отклонения от прямолинейного равновесного положения стержня. Величина критической нагрузки зависит от соотношения продольных и поперечных размеров, материала и условий закрепления стержня.

Деформация продольного изгиба стержня может протекать как в упругой стадии, когда критическое напряжение не превышает предела упругости материала, так и в пластической стадии, когда критическое напряжение превышает предел упругости. Величина критической силы рассчитывается в этих случаях по-разному.

В случае упругого продольного изгиба критическая сила рассчитывается по формуле Эйлера:

,

где Е – модуль продольной упругости, МПА;

I_min - минимальный осевой момент инерции поперечного

сечения стержня, м⁴.

В нашем случае при прямоугольном сечении

,

где h и b – большая и меньшая сторона сечения;

L – длина стержня;

μ – коэффициент, учитывающий условия закрепления

стержня.

Формула Эйлера применима, когда

или гибкость стержня

,

где – минимальный радиус инерции сечения стержня, м;

σ_пц – предел пропорциональности материала стержня, МПа.

Экспериментальное значение прогиба стержня определяется на основе формулы Энгессера. Реальный стержень всегда имеет начальный прогиб, обусловленный неточностью его изготовления. Рассмотрим деформацию стержня, имеющего первоначальный прогиб в середине f₀ под действием продольной силы F.

Рис. 1. Схема стержня с начальным прогибом

Уравнение линии начального прогиба (А)

Уравнение линии дополнительного прогиба под действием продольной силы F (B)

Дифференциальное уравнение прогибов изогнутой оси сжатого стержня (С)

После подстановки (А) и (В) в (С) получим:

или

Откуда получим формулу Энгессера