ЛАБА 1 ПК

Федеральное агентство связи

Ордена трудового красного знамени федеральное государственное

бюджетное образовательное учреждение высшего образования

«Московский технический университет связи и информатики»

Кафедра Радиотехнических систем

Лабораторная работа №5

«Построение и исследование схем дискретной логики, используемых при создании помехоустойчивых кодеков (схемы умножения и деления полиномов, а также генератора псевдослучайных последовательностей)»

Выполнил студент:

Епифанов Г.Ю

Проверила:

Минаева О.Н

Цель работы:

Изучение принципа построения и работы схем дискретной логики, используемых при создании помехоустойчивых кодеков

ВАР-6

Исходные данные:

ЕГ = 0010100011

a(x)=x⁷+x⁵+x+1

Образующий полином из таблицы №2

g(x)=113₈= 1001011₂=x⁶+x³+x+1

Предварительный расчёт:

1. Умножим исходный полином на образующий

c(x)=a(x)*g(x)= (x⁷+x⁵+x+1)*( x⁶+x³+x+1)= x¹³+x¹¹+ x¹⁰ +x⁵+x⁴+x³+ x²+1

10110000111101=C

2. Произведём деление с(x)/g(x)

Ход работы:

1. Построение регистра сдвига битовых последовательностей.

Регистр сдвига битовых порследовательностей

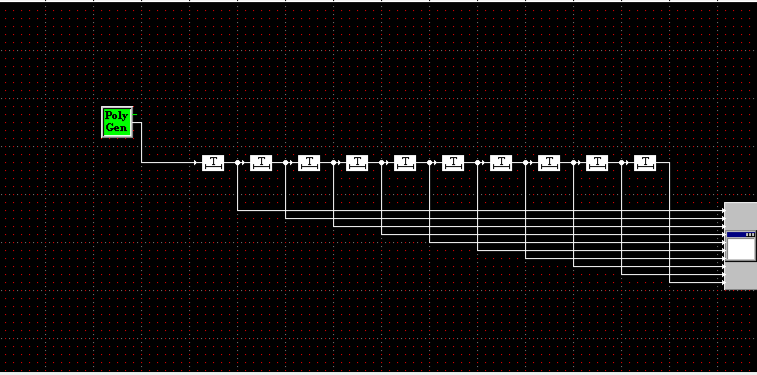
Данные битовой консоли для регистра сдвига

Сохранённые бинарные данные представлены ниже, в них тоже видна периодически повторяющаяся входная последовательность за исключенеим того, что она выходит младшими битами вперёд, а в начале последовательности есть нулевые биты, соответствующие выходу заранее заданных нулевых состояний регистров сдвига.

2. Построение схемы перемножения полиномов-битовых последовательностей.

2.1 Перемножитель полиномов-битовых последовательностей по схеме Фибоначчи.

g(x)=113₈= 1001011₂=x⁶+x³+x+1

Выходная последовательность, соответствует предварительно рассчитанному произведению c=a*g=10110000111101

2.2 Схема Галуа для перемножения полиномов

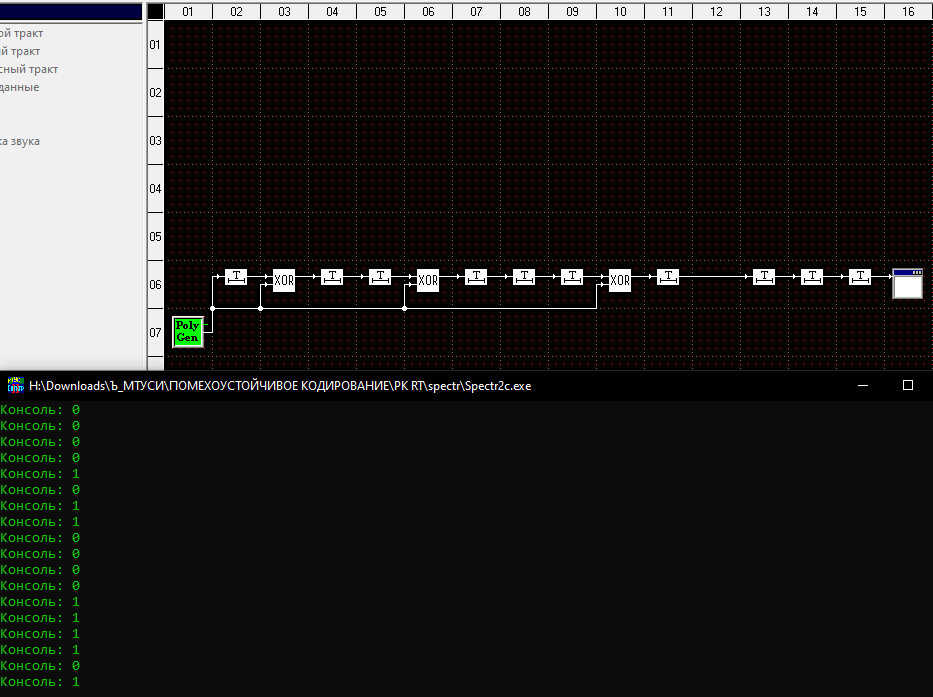
3 Построение схем для деления полиномов

3.1 Схема Фибоначчи для деления полиномов

3.2 Схема Галуа для деления полиномов

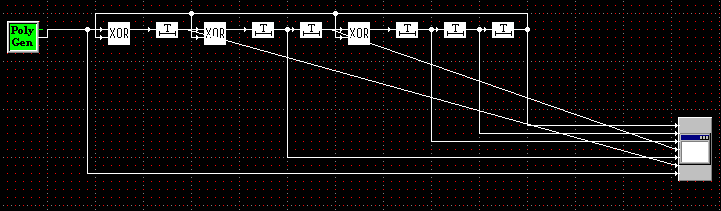
4.1 Генератор псевдослучайной последовательности по схеме Фибоначчи

4.2 Генератор псевдослучайной последовательности по схеме Галуа

Выводы:

1. Изучен принцип работы умножителя многочленов на элементах дискретной логики по схемам Галуа и Фибоначчи. Результаты, полученные с помощью лабораторного стенда совпали с даннвми предварительного расчёта.

2. Изучен принцип работы делителя многочленов на элементах дискретной логики по схемам Галуа и Фибоначчи. Результаты, полученные с помощью лабораторного стенда совпали с данными предварительного расчёта

3. На базе схем деления полиномов построены схемы генераторов псевдослучайных последовательностей. Период ПСП генерируемой по лабораторному заданию равен (не равен) максимально возможному значению 2ⁿ-1, где n –порядок образующего многочлена g(x).

Москва 2024