Вопрос 1: Анализ условий самовозбуждения автогенератора.

1. Анализ условий самовозбуждения автогенератора.

Структурная схема автогенератора имеет вид:

 

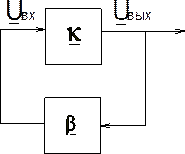
Состоит из усилителя с коэффициентом усиления   и звена положительной обратной связи 

Коэффициенты   и   зависят от частоты и являются комплексными числами.

В качестве звеньев ОС используются частотно зависимые цепи: LC-контуры, либо RC-четырехполюсники.

Если   и   представляют колебания синусоидальной формы, то устойчивый стационарный режим, при котором амплитуды   возможен при условии   – условие самовозбуждения. 

Действительно:   

Откуда следует: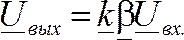 

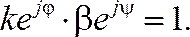
где   и   – модули коэффициентов усиления,

 и   – аргументы этих коэффициентов.

Равенство     = 1 выполняется при следующих условиях:

1) 

2) 

где 

Условие 1 называется условием баланса амплитуд. Оно соответствует тому, что потери энергии в автогенераторе восполняются звеном ПОС от источника питания.

Условие 2 называется условием баланса фаз. Оно свидетельствует о наличии положительной обратной связи.

Вопрос 2: z-преобразование дискретных функций и его свойства.

Рассмотрим, в качестве примера, z- преобразование дискретной функции единичного скачка, заданной выражением :

Последняя формула записана, исходя из того, что полученная сумма является суммой бесконечной геометрической прогрессии.

Свойства Z–преобразования

БИЛЕТ № 25

Вопрос 1: Узкополосные сигналы. Понятие аналитического сигнала. 1.

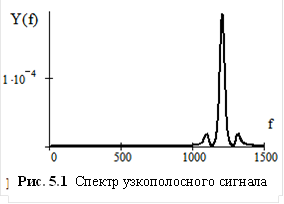
В измерительных информационных системах и в различных системах передачи информации часто используются сигналы, спектр которых сосредоточен в узком диапазоне частот  , ширина которого   намного меньше среднего значения частоты   (рис. 5.1). Сигнал, спектр которого соответствует рис. 5.1, расположен в полосе частот примерно от 1000 до 1400 Гц. Полоса частот, занимаемая сигналом, равна 400 Гц, среднее значение частоты составляет 1200 Гц

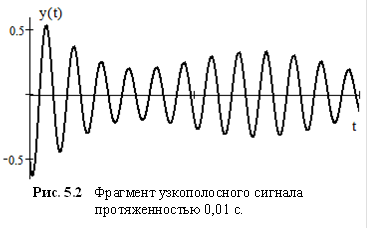Подобные сигналы, имеющие форму почти гармонического колебания, у которого амплитуда и фаза изменяются во времени, и называются узкополосными сигналами (рис. 5.2). В каждый момент времени t значение такого сигнала x(t) можно рассматривать как значение некоторой придуманной для этого момента времени косинусоиды  , амплитуда   и начальная фаза   которой различны для каждого момента времени t, а частота равна среднему значению из частотного диапазона сигнала. Такого рода узкополосный сигнал можно представить в виде выражения: .

Переменная во времени амплитуда А(t) называется в этом случае амплитудной огибающей сигнала, начальная фаза φ(t) – фазовой функцией сигнала x(t), а весь аргумент косинуса – полной фазой сигнала: .

Амплитудную огибающую А(t) в первом приближении можно представить себе в виде кривой, скользящей по вершинам сигнала. Фазовая функция не допускает такой простой интерпретации. По графику сигнала довольно просто восстановить форму амплитудной огибающей, но построить алгоритм выполнения этой процедуры достаточно сложно. В дальнейшем нашей задачей и будет построение алгоритма определения амплитудной огибающей и фазовой функции сигнала. Практически эта операция реализуется устройствами, которые называются амплитудными демодуляторами.

Представим узкополосное колебание в виде вещественной части комплексной экспоненты:

.

В комплексном выражении, стоящем под скобками, можно выделить два принципиально различных сомножителя:

-   — это гармоническое колебание с высокой частотой  , так называемое несущее колебание,

-   - относительно медленно меняющийся сомножитель, содержащий в себе информацию как об амплитудной огибающей, так и о начальной фазе.

Этот медленно изменяющийся сомножитель и называется комплексной огибающей узкополосного сигнала:

.

Сопоставить одному сигналу x(t) сразу две функции A(t) и φ(t) можно, конечно, очень многими способами. Однако искомое представление должно удовлетворять нескольким очевидным требованиям:

- для гармонического колебания искомая процедура должна дать постоянную амплитуду и постоянную начальную фазу,

- фазовая функция не должна изменяться при умножении сигнала на произвольный множитель.

Этих ограничений достаточно, чтобы построить единственную процедуру выделения амплитудной огибающей и фазовой функции. Эта процедура основывается на использовании еще одного интегрального преобразования – преобразования Гильберта.

Комплексный сигнал, полученный на основе преобразования Гильберта, называется «аналитическим» и записывается в виде выражения, где исходный сигнал есть реальная часть аналитического сигнала.
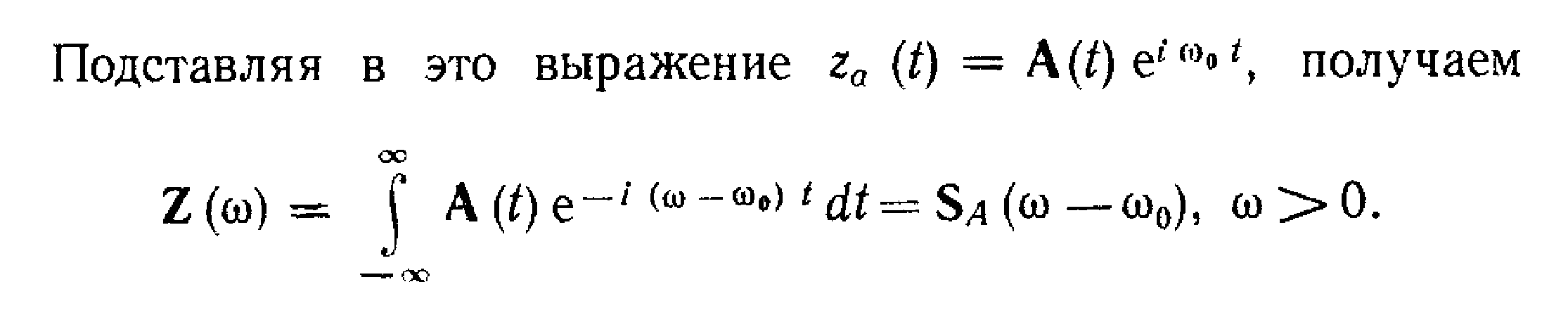