
Ответы на экзамен заочники
.pdf
Тест: "ОТС. Часть 1,2. Экзамен. Заочн.".
Задание №1 Раздел1. 4. Дискретизация сигналов во времени.
Спектр непрерывной функции, которая полностью определяется своими отсчетами, взятыми в моменты времени kT, T=1/2Fm - ?
|
|
Выберите один из 4 вариантов ответа: |
1) |
+ |
не содержит частот выше Fm |
2) |
- |
содержит частоты выше Fm |
3) |
- |
бесконечный |
4) |
- |
не содержит частот меньше Fm |
Задание №2 Раздел1. 4. Дискретизация сигналов во времени.
Интервал дискретизации по теореме Котельникова для сигнала, спектр которого ограничен частотой Fm , равен:
Выберите один из 5 вариантов ответа:
1
1) + 2Fm
2) |
- |
1/Fm |
3) |
- |
Fm |
4) |
- |
2/ Fm |
5) |
- |
2 Fm |
Задание №3 Раздел1. 4. Дискретизация сигналов во времени.
Интервал дискретизации по теореме Котельникова для сигнала, спектр которого ограничен частотой ωm , равен :
Выберите один из 4 вариантов ответа:
1)+
2)-
3)-

4)-
Задание №4 Раздел1. 4. Дискретизация сигналов во времени.
Интервал дискретизации, если спектр сигнала ограничен частотой 500 Гц, равен :
Выберите один из 5 вариантов ответа:
1) |
+ |
1мс |
2) |
- |
2мс |
3) |
- |
500 мс |
4) |
- |
1000 Гц |
5) |
- |
500 Гц |
Задание №5 Раздел1. 4. Дискретизация сигналов во времени.
Интервал дискретизации, если спектр сигнала ограничен частотой 3140 рад/с равен: ?
Выберите один из 4 вариантов ответа:
1) |
+ |
1 мс |
2) |
- |
2 мс |
3) |
- |
0.5 мс |
4) |
- |
1570 рад/с |
Задание №6 Раздел1. 4. Дискретизация сигналов во времени.
Фамилия автора теоремы, в соответствии с которой осуществляется дискретизация функции по времени:
|
|
Выберите один из 5 вариантов ответа: |
1) |
+ |
Котельников |
2) |
- |
Винер |
3) |
- |
Шеннон |
4) |
- |
Фурье |
5) |
- |
Лаплас |

Задание №7 Раздел1. 4. Дискретизация сигналов во времени.
Интервал дискретизации, если частота дискретизации 100 Гц, равен :
Выберите один из 5 вариантов ответа:
1) |
+ |
10мс |
2) |
- |
20 mс |
3) |
- |
100 mс |
4) |
- |
50 Гц |
5) |
- |
10Гц |
Задание №8 Раздел1. 4. Дискретизация сигналов во времени.
Частота дискретизации, если интервал дискретизации 1мс, равна:
|
|
Выберите один из 4 вариантов ответа: |
1) |
+ |
1000 Гц |
2) |
- |
500 Гц |
3) |
- |
250 Гц |
4) |
- |
125 Гц |
Задание №9 Раздел1. 4. Дискретизация сигналов во времени.
Спектр сигнала, для которого интервал дискретизации равен 10мс, ограничен частотой :
|
|
Выберите один из 5 вариантов ответа: |
1) |
+ |
50 Гц |
2) |
- |
100 Гц |
3) |
- |
10мс |
4) |
- |
50 мс |
5) |
- |
50 рад/с |
Задание №10 Раздел1. 4. Дискретизация сигналов во времени.

В соответствии с теоремой Котельникова осуществляется ______?_______
непрерывной функции.
|
|
Выберите один из 4 вариантов ответа: |
1) |
+ |
дискретизация |
2) |
- |
квантование |
3) |
- |
усиление |
4) |
- |
ослабление |
Задание №11 Раздел1. 4. Дискретизация сигналов во времени.
Дляопределенияинтерваладискретизациипо теоремеКотельниковадолжна быть задана ____?____ спектра функции.
|
|
Выберите один из 4 вариантов ответа: |
1) |
+ |
ширина |
2) |
- |
высота |
3) |
- |
длительность |
4) |
- |
полнота |
Задание №12 Раздел1. 4. Дискретизация сигналов во времени.
Сигнал описывается функцией времени u(t)=cos2πt . Отсчеты сигнала, взятые в соответствии с теоремой Котельникова в моменты
времени t=0.5k, k=0,1,2, равны , соответственно:
|
|
Выберите один из 4 вариантов ответа: |
1) |
+ |
1; -1; 1; |
2) |
- |
1; 0; 1; |
3) |
- |
1; 1; 1; |
4) |
- |
0; 1; 0; |
Задание №13 Раздел1. 4. Дискретизация сигналов во времени.
Сигнал описывается функцией времени u(t)=cosπt . Отсчеты сигнала, взятые в соответствии с теоремой Котельникова в моменты времени t=0.5k, k=0,1,2, равны , соответственно :
|
|
Выберите один из 4 вариантов ответа: |
1) |
+ |
1; 0; -1; |
2) |
- |
1; 0; 0; |
3) |
- |
1;1;1; |
4) |
- |
0;1;0; |
Задание №14 Раздел1. 4. Дискретизация сигналов во времени.
По теореме Котельникова отсчеты функции берутся с частотой, которую называют частотой ______?________.
|
|
Выберите один из 4 вариантов ответа: |
1) |
+ |
дискретизации |
2) |
- |
квантования |
3) |
- |
усиления |
4) |
- |
гармоники |
Задание №15 Раздел1. 4. Дискретизация сигналов во времени.
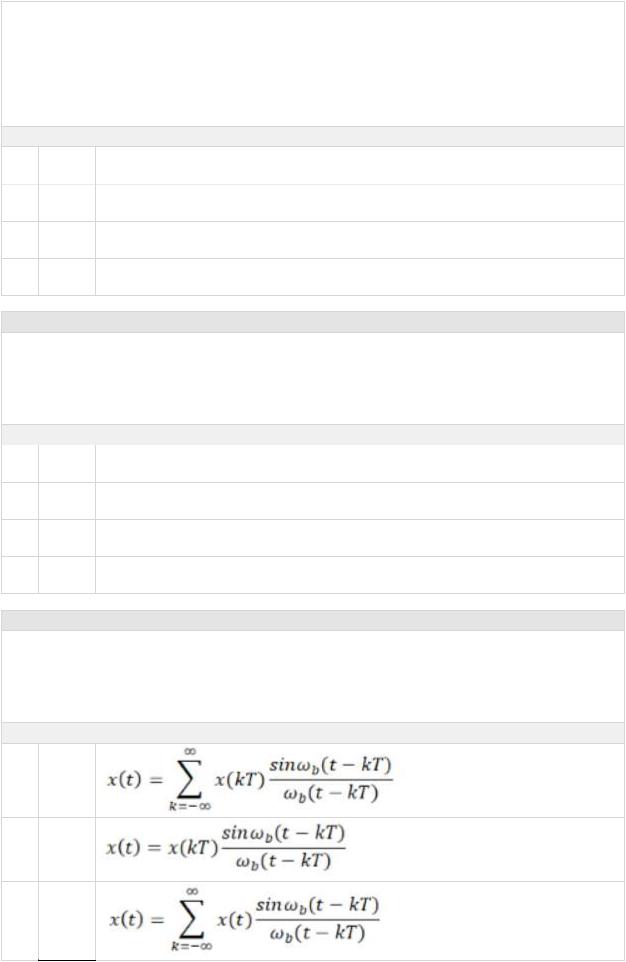
Ряд Котельникова для непрерывной функция с заданной точностью может быть представлен в виде:
Выберите один из 4 вариантов ответа:
1)+
2)-
3)-

4)-
Задание №16 Раздел1. 4. Дискретизация сигналов во времени.
Для восстановления исходной непрерывной функции по ее отсчетам необходимо подать эти отсчеты на вход:
|
|
Выберите один из 4 вариантов ответа: |
1) |
+ |
идеального ФНЧ |
2) |
- |
ФНЧ |
3) |
- |
резонансного контура |
4) |
- |
RC фильтра |
Задание №17 Раздел1. 4. Дискретизация сигналов во времени.
Спектр сигнала ограничен частотой 1000 Гц. Интервал дискретизации в мкс и частота дискретизации в рад/с, соответственно, равны:
|
|
|
|
Выберите один из 4 вариантов ответа: |
|
1) |
+ |
500 |
мкс; 12560 |
рад/с |
|
2) |
- |
1000 |
мкс; 2000 |
рад/с |
|
3) |
- |
500 |
мкс; 6280 рад/с |
||
4) |
- |
1000 |
мкс; 12560 рад/с |
||
Задание №18 Раздел1. 4. Дискретизация сигналов во времени.
Спектр сигнала ограничен частотой 6280 рад/с. Интервал дискретизации в мкс и частота дискретизации в кГц, соответственно, равны:
|
|
|
Выберите один из 4 вариантов ответа: |
1) |
+ |
500 |
мкс; 2 кГц |
2) |
- |
1000 мкс; 2кГц |
|
3) |
- |
500 |
мкс; 6280 рад/с |

4) |
- |
1000 мкс; 12560 рад/с |
Задание №19 Раздел1. 4. Дискретизация сигналов во времени.
Для восстановления непрерывной функции из отсчетов используется
____?_____ ФНЧ
|
|
Выберите один из 4 вариантов ответа: |
1) |
+ |
идеальный |
2) |
- |
реальный |
3) |
- |
RC |
4) |
- |
хороший |
Задание №20 Раздел1. 4. Дискретизация сигналов во времени.
Интервал дискретизации (слева) соответствует ширине спектра сигнала (справа):
Выберите правильные варианты.
Выберите несколько из 4 вариантов ответа:
 1)
1)  +
+
 2)
2)  +
+
 3)
3)  +
+
 4)
4)  +
+
1мс; |
0.5 кГц; |
1c; |
0.5 Гц; |
5 мс; |
100Гц; |
2мкс; |
250 кГц; |
Задание №21 Раздел1.7. Теорема Котельникова
Непрерывный гармонический сигнал имеет вид u(t)=cos2π*103t. Интервал дискретизации по теореме Котельникова и первые три отсчета, начиная с момента t=0 , соответственно, равны: ?
|
|
|
Выберите один из 5 вариантов ответа: |
1) |
+ |
0.5 |
мс; 1; -1; 1; |
2) |
- |
0.5 |
мс; 0; 1; 0; |
3) |
- |
1мс; 1; -1; 1; |
|
4) |
- |
0.5 |
мс; 1; 0; 1; |
5) |
- |
1 мс; 0; -1; 1; |
|

Задание №22 Раздел1.7. Теорема Котельникова
Непрерывный гармонический сигнал имеет вид u(t)=cos2π*104t. Максимальная частота в спектре этого сигнала и первые три отсчета, начиная с момента t=0 , соответственно, равны : ?
|
|
|
Выберите один из 4 вариантов ответа: |
1) |
+ |
104 |
Гц ; 1; -1; 1; |
2) |
- |
10 кГц ; 1; 0; 1; |
|
3) |
- |
104 |
Гц ; 1; 1; 1; |
4) |
- |
104 |
рад/с ; 1; -1; 1; |
Задание №23 Раздел1.7. Теорема Котельникова
Ширине спектра функции (слева) соответствует интервал дискретизации (справа):
Установите соответствие.
|
|
Укажите соответствие для всех 4 вариантов ответа: |
||||
1) |
1 |
0.1 кГц; |
1) |
5 мс; |
||
2) |
2 |
1 |
мГц; |
2) |
0.5 |
мкс; |
3) |
3 |
5 |
Гц; |
3) |
0.1 |
с; |
4) |
4 |
0.25 Гц; |
4) |
2с ; |
|
|
Задание №24 Раздел1.7. Теорема Котельникова
Ширине спектра функции (слева) соответствует частота дискретизации (справа):
Установите соответствие.
|
|
Укажите соответствие для всех 4 вариантов ответа: |
|||
1) |
1 |
0.1 кГц; |
1) |
0.2 кГц ; |
|
2) |
2 |
1 мГц; |
2) |
12.56*106 рад/с ; |
|
3) |
3 |
31,4 |
р/с ; |
3) |
10 Гц ; |
4) |
4 |
0.25 |
Гц; |
4) |
3.14 рад/с ; |
Задание №25 Раздел1.7. Теорема Котельникова

Ширине спектра функции, дискретизированной в соответствии с теоремой Котельникова (слева), соответствует полоса пропускания идеального ФНЧ (справа) :
Установите соответствие.
|
|
Укажите соответствие для всех 4 вариантов ответа: |
|||
1) |
1 |
0.1 кГц; |
1) |
0.1 кГц ; |
|
2) |
2 |
1 мГц; |
2) |
6.28*106 рад/с ; |
|
3) |
3 |
31,4 |
р/с ; |
3) |
5 Гц ; |
4) |
4 |
0.25 |
Гц; |
4) |
1.57 рад/с ; |
Задание №26 Раздел1.7. Теорема Котельникова
Установите порядок следования символов из набора в формуле, определяющей интервал дискретизации по теореме Котельникова:
|
|
Укажите порядок следования всех 5 вариантов ответа: |
1) |
5 |
2Fв |
2) |
2 |
= |
3) |
3 |
1 |
4) |
4 |
/ |
5) |
1 |
Т |
Задание №27 Раздел1.7. Теорема Котельникова
Установите порядок следования символов из набора в формуле, определяющей интервал дискретизации по теореме Котельникова:
|
|
Укажите порядок следования всех 5 вариантов ответа: |
1) |
3 |
π |
2) |
2 |
= |
3) |
1 |
Т |
4) |
5 |
ωв |
5) |
4 |
/ |
Задание №28 Раздел1.7. Теорема Котельникова

Установите порядок следования символов в формуле, определяющей частоту дискретизации по теореме Котельникова:
|
|
Укажите порядок следования всех 5 вариантов ответа: |
1) |
5 |
Fв |
2) |
3 |
4 |
3) |
2 |
= |
4) |
1 |
ωд |
5) |
4 |
π |
Задание №29 Раздел1.7. Теорема Котельникова
Установите порядок следования символов в разложении функции в ряд Котельникова:
 1)
1)  2
2
2)5
 3)
3)  4
4
 4)
4)  1
1
5)3
Укажите порядок следования всех 5 вариантов ответа:
=
sin в (t kT)
в (t kT)
x(kT)
x(t)
Задание №30 Раздел1.7. Теорема Котельникова
Непрерывный гармонический сигнал имеет вид u(t)=0.5cos2π*104t. Интервал дискретизации по теореме Котельникова и первые три отсчета, начиная с момента t=0 , соответственно, равны ____ мс, ___, ___, ___:
Введите интервал дискретизации и первые три отсчета в формате Х,ХХ
Запишите число:
1) |
интервал |
0,05 |
дискретизации мс |
||
2) |
отсчет 1 мс |
0,5 |
3) |
отсчет 2 мс |
-0,5 |
4) |
отсчет 3 мс |
0,5 |
Задание №31 Раздел1.7. Теорема Котельникова
Амплитудный спектр непрерывного сигнала имеет вид: |
S(ω)= exp(- |
2ω/α); ω>0; |
|
