ИДЗ / ИДЗ5_ФОИИ

Министерство НАУКИ И ВЫСШЕГО образования Российской Федерации

Федеральное государственное автономное образовательное учреждение высшего образования

«Национальный исследовательский Томский политехнический Университет»

Инженерная школа новых

производственных технологий

Отделение материаловедения

Направление 12.03.02 «Оптотехника»

ИНДИВИДУАЛЬНОЕ ДОМАШНЕЕ ЗАДАНИЕ № 5

Вариант 6

по дисциплине:

ФИЗИЧЕСКИЕ ОСНОВЫ ИСТОЧНИКОВ ИЗЛУЧЕНИЙ

Исполнитель:
студент группы	4В01		Деньгуб А.Р.
Руководитель:
преподаватель			Штанько В. Ф.

Томск - 2023

Задание

1. Рассмотреть расщепление головных групп линий при комбинации P и D термов в слабом магнитном поле для атомов (ионов): согласно варианту Si⁺².

2. Определить изменение энергии и поляризацию излучения.

Решение

Ион в соответствии с вариантом – Si⁺².

Электронная конфигурация иона выглядит как:

1s² 2s² 2p⁶ 3s² 3p⁰

Рассмотрим схему термов иона Si⁺²

Терм основного состояния

, , , , ,

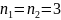
Согласно, принципу Паули возможными состояниями являются те, которые отличаются хотя бы одним из квантовых чисел. Поскольку n, l, m_l для двух электронов одинаковы, поэтому m_s1 = ½, m_s2 = - ½, а следовательно, S = 0. Полный механический момент: J = 0.

Мультиплетность

Получим основной терм:

Переведем один из электронов в возбужденное состояние n = 3, L = 1

, , , , ,

Так как электроны теперь отличаются квантовым числом l, каждое из квантовых чисел m_s1 и m_s2 может принимать значения ±½. Тогда S = 0, 1.

Мультиплетность:

Полный механический момент:

J₁ = |L + S| = 1;

J₂ = |L + S|, |L + S – 1|, |L – S| = 2, 1, 0.

Синглетный терм:

Триплетный терм:

Следующее возбужденное состояние n = 3, L = 2

, , , , ,

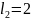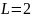Мультиплетность:

Полный механический момент

J₁ = |L + S| = 2;

J₂ = |L + S|, |L + S – 1|, |L – S| = 3, 2, 1.

Синглетный терм: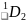

Триплетный терм:

• Интересующими нас состояниями являются:

Синглетные термы: ,

Триплетные термы: , .

Рассмотрим расщепление линий, в слабом магнитном поля, для триплетных и синглетных термов отдельно.

1. Синглетные термы

Так как S = 0, мы будем наблюдать нормальный эффект Зеемана.

Значения добавочной энергии

Где

Правило отбора примет вид:

компонента (обозначена на схемах синим цветом) (электрический вектор световой волны совершает линейные колебания, параллельные направлению вектора магнитной напряженности )

компонента (электрический вектор световой волны совершает круговые колебания в плоскости, перпендикулярной направлению вектора магнитной напряженности )

Рис.1 Расщепление синглетных P и D термов в слабом магнитном поле. Синим отмечены переходы 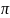-компонент, черным – -компонент.

2. Триплетные термы

Так как S = 1, мы будем наблюдать аномальный (сложный) эффект Зеемана.

Значения добавочной энергии

Где множитель Ланде

Квантовое число принимает значения

Т.е всего значений

Правило отбора примет вид:

компонента (обозначена на схемах синим цветом) (электрический вектор световой волны совершает линейные колебания, параллельные направлению вектора магнитной напряженности )

компонента (электрический вектор световой волны совершает круговые колебания в плоскости, перпендикулярной направлению вектора магнитной напряженности )

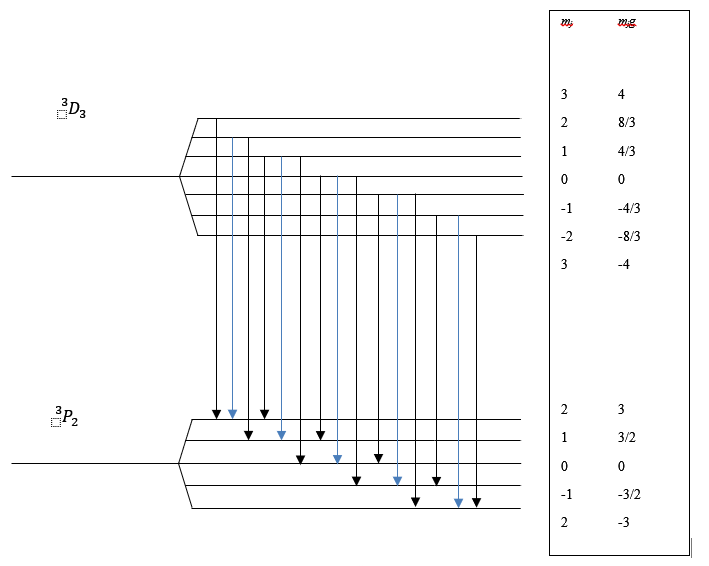
Рис.2 Расщепление триплетных и термов в слабом магнитном поле.

Рис.3 Расщепление триплетных и термов в слабом магнитном поле.

Рис.4 Расщепление триплетных и термов в слабом магнитном поле.

1. Определим изменение энергии и поляризацию излучения. 

1. При отсутствии магнитного поля реализуются следующие переходы

Синглетные термы

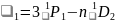
При

Триплетные термы

При

Определим множитель Ланде для найденных термов

Для синглетных термов:

Терм -

Терм - , ;

Для триплетных термов:

Терм - , ;

Терм - .

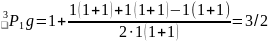Терм - , ;

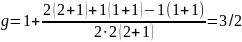Терм -

Терм - , ;

Терм - .

Определим изменение энергии для синглетных термов

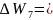
Следовательно, в слабом магнитном поле для синглетных термов получим 3 линии (нормальный эффект Зеемана)

2. Изменение энергии для триплетных термов

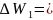
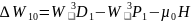
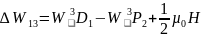
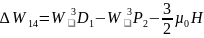
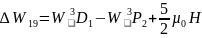
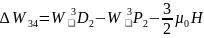
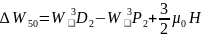
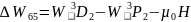
Следовательно, в слабом магнитном поле для триплетных термов получим 65 линий (сложный эффект Зеемана).

Вывод: расщепление на три компоненты спектральных линий наблюдается в том случае, когда можно пренебречь спиновым моментом электрона или когда S = 0, т. е. линии одиночных серий. В остальных случаях в магнитном поле наблюдается сложный (или аномальный) эффект Зеемана (Явление расщепления линий спектра излучения при помещении атома в слабое внешнее магнитное поле). Характерным для сложного эффекта Зеемана является расщепление линий в магнитном поле на большое число компонент, причем расщепление переменно и равно рациональной дроби от нормального зеемановского расщепления.