

|
Пример 6.2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Формула (6.18) значительно упрощается, если оценка находится |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Вычислить приближенное значение производной функции, за- |
|
|
|
для значения производной |
|
f ′(x) |
в узле xi |
|
|
|
таблицы. В этом случае, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
данной таблицей 6.2 в точке х=4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
учитывая (6.14), получаем: |
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 6.2 |
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n−i |
|
|
|
|
n |
|
i!(n−i)1 |
|
|
|
(n+1) |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
x |
|
=R |
|
x |
|
|
= |
|
−1 |
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
ξ |
, |
|
|
|
(6.19) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
x |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
n |
( i ) |
|
n |
( |
|
|
) |
|
|
( |
|
|
|
|
) |
|
|
|
|
|
|
|
|
(n+1)! |
|
|
|
|
|
( ) |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
f(x) |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
–1 |
|
|
|
|
|
|
|
6 |
|
|
|
|
|
где ξ– промежуточное значение между x0,x1,x2,…,xn . |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Используя формулу (6.16), получим (n = 2, h = 1): |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
Обозначив: |
|
|
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
1 |
|
d (t −1)(t −2) |
|
|
|
|
−1 |
d (t −2) |
|
|
1 |
|
d t(t −1) |
|
|
|
ГMn+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(n+1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
f ′(x) ≈2 |
|
|
|
|
|
|
|
−( |
|
|
) |
|
|
|
|
|
+6 |
|
|
|
|
|
= |
|
|
|
= max |
|
f |
|
|
|
(x) |
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
dt |
|
|
|
|
|
|
|
dt |
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
2! |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 ≤x≤xn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
получим верхнюю оценку абсолютной ошибки численного диффе- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
=(t −2+t −1) =(t −2+t)+3(t −1+t) =2t −3+2t −2+6t −3=10t −8. |
|
|
|
ренцированияБв узлах: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
Учитывая, что узел х=4 соответствует значению t=1, т. е. |
|
|
й |
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
Mn+1 |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
r |
x |
|
|
|
≤ |
|
(n+1)! |
h i! |
n |
−i |
!. |
|
|
|
|
|
|
|
(6.20) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x − x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
i ) |
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
t = |
→ f |
′ |
(4) ≈ 2. |
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6.2.4. Численное дифференцирование |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
на основе интерполяционной формулы Ньютона |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Если известно аналитическое выражение функции f(x), то ф р- |
р |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
мулу для оценки погрешности |
|
численного |
дифференцир вания |
|
Запишем для функции f(x), заданной своими значениями в рав- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
можно при этом же условии получить на основе формулы п греш- |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ноотстоящих узлах x0,x1,x2, … ,xn первый интерполяционный |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ности интерполирования: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (n+1) (ξ) |
|
|
|
|
|
|
|
|
|
|
многочлен Ньютона: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
R |
(x) = f (x)−F |
(x) = |
|
|
Π |
|
(x) |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t(t −1) 2 |
|
|
|
|
|
t(t −1)(t −2) 3 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
(6.17) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
n |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
n+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(n+1)! |
|
|
|
|
|
|
|
т |
|
|
|
Pn (x) =Pn (x0 +th) = y0 +t y0 + |
2! |
|
|
|
|
y0 − |
|
|
|
|
|
|
|
|
3! |
|
|
|
|
|
y0 +…+ |
||||||||||||||||||||||||||||||||||
где ξ = ξ(x) – значение из отрезка [a; b], |
|
|
|
|
|
|
отиу лов х. |
|
|
|
|
|
|
|
|
|
+ |
t(t −1) … (t −n+1) |
|
|
n y0. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
Учитывая (6.7) и допуская, что f(x) дифференцируемаз |
п + 1 раз, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
Перепишем этот полином, производя перемножение скобок: |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
запишем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
отличнd ое(n+1) |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pn (x0 +th) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
′ |
(x) = |
|
|
(n+1) |
|
|
|
|
(ξ) |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
3 |
|
|
2 |
|
|
|
|
|
||||||||||||||||||||||||
|
rn (x) =Rn |
|
|
f |
|
|
|
|
|
(ξ)Π`n+1(x) |
|
f |
|
|
|
|
, (16.18) |
|
|
|
|
t |
|
−t |
|
|
|
|
|
t |
|
|
−3t |
|
|
+2t |
|
|
|
|
|
|
t |
|
|
|
−6t |
|
|
+11t |
|
−6t |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
(n+1)! |
|
|
|
п |
|
|
|
dx |
|
|
|
|
|
|
|
|
|
= y0 +t y0 + |
|
|
|
|
2y0 |
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3y0 + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4y0 |
+… |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
3! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24 |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
261 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
262 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Дифференцируя P (x +th) поt, получиманалогичноформуле(6.16): |
|
|
|
|
|
|
n ( ) ( |
) |
n |
hn |
|
|
|
|
+ |
( ) |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
n |
|
|
0 |
|
|
′ |
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n+1 |
|
(n |
1) |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
x = −1 |
|
|
|
|
|
|
f |
|
|
|
|
ξ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) ≈Pn (x0 +th) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(n+1) |
|
|
|
|
|
|
У |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На практике f |
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
y + |
2t −1 |
2y |
|
3t |
2 |
|
−6t +2 |
3y |
|
|
|
2t |
3 |
−9t |
2 |
+11t −3 |
4y |
|
|
|
(6.21) |
|
|
|
приближенно полагают: |
Т |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
= |
|
h |
|
2! |
|
− |
|
|
|
|
|
6 |
|
|
|
+ |
|
|
|
|
12 |
|
|
|
|
|
+… . |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (n+1)(ξ) |
≈ |
n+1 |
y |
|
|
|
|
|||||||
Подобным путем можно получить и производные функции f(x) |
|
|
|
Б |
|
|
|
|
n+1 |
0 , |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
более высоких порядков. Однако каждый раз вычисляя значение |
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
производной |
функции f(x) |
|
в фиксированной точке х, |
в качестве х0 |
|
|
|
что позволяет использовать приближенную формулу: |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
следует брать ближайшее слева узловое значение аргумента. |
|
|
|
|
|
|
|
Г |
|
|
|
|
−1 n Δn+1y |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
Формула 6.21 существенно упрощается, если исходным значе- |
|
|
|
|
|
|
|
rn (x0 ) ≈ |
( |
|
) |
|
|
|
|
|
0 . |
|
(6.24) |
|||||||||||||||||||||||||||||||||||||||||||||||
нием х оказывается один из узлов таблицы. Так как в этом случае |
|
|
|
|
|
|
|
|
|
|
|
|
h(n+1) |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
каждый узел можно считать начальным, то принимая х = х0, t = 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6.2.5. Постановка задачи численного интегрирования |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
f ′(x0 ) = |
1 |
y0 − |
2 y0 + |
|
3 y0 − |
|
4 y0 + |
5 y0 … . |
|
|
|
(6.22) |
р |
йПри вычислении определенного интеграла: |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
h |
|
|
|
|
2 |
|
|
|
3 |
|
|
|
|
|
|
4 |
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
Эта формула позволяет точно получать значения производных |
|
и |
|
|
|
|
I1= |
b |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
a |
∫ f (x)dx, |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
Rn (x) =h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
(ξ), |
|
|
|
|
мно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
функций, заданных таблично. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Выведем формулу погрешности дифференцирования. Исп льзуя |
|
|
|
где f(x) – непрерывная на отрезке [a; b] |
функция, иногда удается |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
формулу (6.17) применительно к первому интерполяционному |
|
- |
|
|
|
воспользоваться формулой Ньютона–Лейбница: |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
гочлену Ньютона, запишем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
n+1 t(t −1)(t −2)…(t −n) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=F(b)−F(a). |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
(n+1) |
|
|
|
|
|
|
|
|
|
|
|
|
∫ f (x)dx |
(6.25) |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(n+1)! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь F(x) – одна из первообразных функции f(x). Однако даже |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
где |
ξ – |
промежуточное |
|
|
значение |
|
|
между |
|
x0,x1,x2, …, |
xn |
|
|
|
в тех |
редких случаях, когда первообразную удается |
явно найти |
|||||||||||||||||||||||||||||||||||||||||||||||||
и заданной точкой х. Предполагая, что f(x) дифференцируема п + 1 |
|
|
|
в аналитической форме, не всегда удается довести до числового от- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
вета значение определенного интеграла. Если учесть, что подынте- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
(xi ) |
|
|
|
||||||||||||||||||||||||
раз, получим для оценки погрешности дифференцирования |
rn |
|
|
|
гральная функция задается таблицей или графиком, то интегриро- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
п |
|
з |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вание |
по формуле |
(6.25) не |
|
|
|
|
получает широкого |
применения |
|||||||||||||||||||||||||||||||
(по аналогии с формулой (6.18)): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
′ |
|
|
|
hn |
|
|
|
(n+1) |
|
|
d |
|
(n+1) |
|
|
|
(n+1) |
d |
|
(n+1) |
|
|
|
|
|
|
|
|
на практике. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
rn (x) =Rn (x) = |
|
|
|
|
|
е |
|
|
t |
|
|
|
|
+t |
|
|
|
|
|
|
f (ξ) |
|
. |
(6.23) |
|
|
|
В подобных случаях применяют различные методы численного |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
f |
|
|
(ξ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
(n+1)! |
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
оdt |
|
|
|
|
|
|
|
|
|
|
интегрирования. Формулы, используемые для вычисления одно- |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
кратных интегралов, называют квадратурными формулами. |
||||||||||||||||||||||||||||
Для случая оценки погр шности в узле таблицы получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
263 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
264 |
|
|
|
|
|
|
|
|
|
|||||
Прием построения квадратурных формул состоит в том, что |
|
|
|
Длина xi+1 −xi =h, i =1,2,…,n −1 |
|
называется шагом интегрирования. |
||||||||||||||||||||||||||||||||||||||||||||||||||
подынтегральная функция f(x) заменяется на отрезке [a; b] интер- |
|
|
|
Естественно считать, что шаг h постоянен, т.е.: |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
поляционным многочленом, например, многочленом Лагранжа |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
Ln (x), и получается приближенное равенство |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h = |
b−a |
. |
|
|
|
|
|
||||||||||||
|
b |
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
||||
|
|
f (x)dx ≈ L |
(x)dx. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
∫ |
|
|
|
|
|
(6.26) |
|
|
|
|
|
|
|
|
|
|
|
|
|
Т |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
∫ n |
|
|
|
|
|
|
|
|
|
|
|
|
В этом случае можно применить интерполяционную формулу |
||||||||||||||||||||||||||||||||||
|
a |
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Лагранжа для равноотстоящих узлов. Итак, с учетом (6.12) и (6.14) |
|||||||||||||||||||||||||||||||
Предполагается, что отрезок |
|
[a; b] |
|
разбит на п частей точка- |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
формула (6.28) для весовых коэффициентов Ai примет вид: |
|
||||||||||||||||||||||||||||||||||||||||||||||||||
миa =x0, x1, x2,…, xn =b, наличие которых подразумевается при по- |
|
|
|
|
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
A |
xn |
|
|
(-1)n-i t[n+1] |
|
|
dx, i =1,2,…,n −1 . |
|
|||||||||||||||||||||||||||||||||||||||||||||
строении многочлена L |
(x). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Гi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
n |
|
(x) (6.10), получим: |
|
|
|
|
|
|
|
|
|
|
|
x∫0 |
i!(n - i)!(t - i) |
|
|
|
|
|
|
|
|
|
|
|
|
(6.29) |
|||||||||||||||||||||||||||
Подставляя вместо Ln |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Пере дем в этом интеграле к переменной t. Из подстановки (6.9) |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
Πn+1 (x) |
|
|
|
|
|
|
|
Πn+1 (x) |
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
b |
b n |
|
|
|
|
|
|
|
n |
b |
|
|
|
|
|
|
получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
∫f (x)dx ≈∫∑yi |
|
|
|
|
|
|
|
|
|
dx =∑yi ∫ |
|
|
|
dx. |
|
|
|
й |
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b-a |
|
|
||||||||||||
|
|
|
− |
|
|
Π |
|
|
|
− |
Π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
a |
a i=0 |
|
|
(x |
|
xi ) |
|
`n+1(x) |
|
i=0 |
a (x |
|
|
xi ) `n+1(x) |
|
|
|
|
dt = |
|
|
|
|
, |
|
|
|
|
|
dx =hdt = |
|
|
dt. |
|
||||||||||||||||||||||
Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
т.е. |
n |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
При х = х0 имеем t = 0, а при х = хn будет: |
|
|
|||||||||||||||||||||||||||||||
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
∫ f (x)dx≈∑yi Ai , |
|
|
|
|
|
|
(6.27) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
р |
|
|
|
|
|
|
|
|
|
|
|
|
t = |
|
xn - x0 |
|
=n. |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
a |
|
|
|
|
i=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
b |
|
|
Пn+1 (x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
||||||||||||||||
|
A = |
|
|
|
dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
где |
|
∫a (x − xi )Пn′+1 (x) |
|
|
|
|
|
(6.28) |
|
|
|
Тогда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
В формуле 6.27 коэффициенты Ai |
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
не |
|
|
|
|
от функц |
|
f(x), |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
n-i |
|
[ |
n |
+1 |
|
|
|
|
|
|
|
|||||||||||||||||||
так как они составлены только с учетом у лов интерполяцт. Если |
|
|
|
|
|
b - a |
|
|
|
|
( |
-1 |
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
Ai = |
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
dt = (b |
- a)Hi , |
|
||||||||||||||||||||||||||||||||
f(x) – полином степени |
п, |
то формула (6.27) |
точная, так как |
|
|
|
|
|
|
|
n |
|
|
|
0∫0 i!(n - i)!(t - i) |
|
|
|
|
(6.30) |
||||||||||||||||||||||||||||||||||||
Ln (x)≡ f (x). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
1 |
n |
( |
-1) |
n-i |
t |
[n+1] |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
Hi = |
|
n 0∫0 |
i!(n - i)!(t - i) |
dt, i = 0,1,2,…,n |
(6.31) |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
6.2.6. Квадратурные формулы Ньют на – К теса |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
зависят |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Применение формулы (6.26) |
ред |
|
лагает п строение на от- |
|
|
|
Числа (6.29) называют коэффициентами Котеса. Они не зависят |
|||||||||||||||||||||||||||||||||||||||||||||||||
резке интегрирования |
|
|
[a; b] |
|
|
системы |
|
|
|
|
интерполяции |
|
|
|
от функции f(х), а только от числа точек разбиения. Окончательно, |
|||||||||||||||||||||||||||||||||||||||||
a =x0, x1, x2 , …, |
xn =b, |
|
|
|
|
|
|
|
|
|
|
узлов |
|
|
|
|
|
|
|
с учетом формул (6.27) и (6.30) получаем следующий вид квадра- |
||||||||||||||||||||||||||||||||||||
которыми отрезок делится на п частей. |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
турных формул Ньютона - Котеса: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
265 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
266 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ f (x)dx ≈ (b − a)∑yi Hi , |
|
|
|
|
|
|
|
|
(6.32) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
i=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ f (x)dx = ∫ Ln (x)dx + Rn (f ), |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
дающих на одном участке интегрирования различные представле- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
где Rn (f ) – остаточный член квадратурной формулы (6.34). Фор- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ния различного числа п отрезков разбиения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
мулу остаточного члена получимТвначале для отрезка [x0 ; x1 ]. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
6.2.7. Формула трапеций |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R = |
1 |
f (x)dx − hА(y + y )= |
0 |
f (x)dx − h (f (x )+ f (x + h)), |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
При п=1 из формулы (6.31) имеем: ( i |
|
0; 1): |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
+h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
1 |
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
1 t |
( |
t − |
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
0 |
|
∫ |
|
|
|
|
) |
|
|
∫ |
( |
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
откуда следует, что естественно рассматривать R как функцию ша- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
H |
|
= − |
|
|
|
|
t |
|
|
dt = − |
|
|
|
t |
− |
1 dt |
= ; |
|
|
|
|
|
|
й |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
га h: R=R(h). Заметим, что R(0)=0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Продифференцируем R(h) по h: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
H1 |
|
= ∫tdt = |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
Б |
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( ) |
|
x0 +h |
|
|
( ) |
|
|
|
|
|
1 |
( |
|
( 0 ) |
|
|
|
|
( 0 |
|
|
|
)) |
|
h |
( |
|
|
|
( |
0 |
)) |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|||||||||||||||||||||||||
Тогда по формуле (6.32) на отрезке [x0 ; x1 ] |
получаем интеграл: |
|
|
R |
h |
= |
|
f x dx − |
|
2 |
|
f x + f x + h − |
2 |
|
|
f |
|
x + h |
|
= |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
∫1 |
f (x)dx = (x1 − x0 )(H0 y0 + H1 y1 ) = |
h |
(y0 + y1 ), |
|
|
|
|
|
|
|
= f (x0 +h) |
− |
|
|
|
f |
|
(x0 |
+h)− |
|
f (x0 )− |
|
f ′(x0 |
|
+ h) = |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
(6.33) |
|
|
|
|
|
|
2 |
2 |
2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
р |
|
|
|
|
|
|
|
|
|
= |
|
( f (x0 +h)− f (x0 )) |
− |
|
f ′(x0 +h). |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
Формула (6.33) дает один из простейших способов вычисления |
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
определенного интеграла и называется формулой трапеций. |
|
- |
|
Заметим, что R`(0)=0. Далее: |
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
вительно, при п=1 подынтегральная функция заменяе ся |
ерпо- |
|
|
|
R′′(h)= |
1 |
f ′(x0 |
|
|
+ h)− |
1 |
f ′(x0 |
+ h)− |
f ′′(x0 |
+ h)= − |
f ′′(x0 + h) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ин |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
(6.35) |
||||||||||
ляционным многочленом Лагранжа первой степени (т.е. линейной |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
функцией), а геометрически это означает, что площадь кр воли- |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
з |
Дейст |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
нейной фигуры заменяется площадью трапеции. |
|
|
|
|
|
|
|
Определим R, последовательно интегрируя R′′(h) на от- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Распространяя формулу (6.33) на все отре ки ра б ен я, полу- |
|
|
|
резке [0;h]: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
чим общую формулу трапеций для отрезка [a;b]: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
b |
|
|
|
y0 |
|
|
п |
|
|
|
|
|
|
yn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫R′′(z)dz = R′(h)− R′(0)= R′(h), |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
∫ f (x)dx = h |
|
|
|
|
|
|
|
|
|
+ |
|
. |
|
(6.34) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
2 |
|
+ y1 |
+ y2 |
+…+ yn−1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
откуда с учетом (6.35) имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
формуле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Если аналитическое выраж ние дляоодынтегральной функции |
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
) |
|
∫ |
|
|
|
|
|
( |
|
) |
|
|
|
|
|
|
∫ |
|
|
|
( |
|
0 |
|
|
) |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
известно, может быть поставл н во рос об оценке погрешности чис- |
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
h |
|
|
′′ |
|
|
|
|
|
|
1 h |
|
|
′′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
h = R |
|
|
|
|
z dz = − |
|
|
|
|
|
zf |
|
|
x |
+ z dz. |
|
|
|
(6.36) |
|||||||||||||||||||||||||||||||||
|
|
|
(6.34) (погрешность метода). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 0 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ленного интегрирования по |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
267 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
268 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Применяя к (6.36) обобщенную теорему о среднем, получаем: |
|
|
|
6.2.8. Формула Симпсона |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
h |
|
|
|
|
|
|
h |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
При п = 2 из формулы (6.31) последовательно имеем (i = 0, 1, 2): |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
R′(h) = − |
f ′′ |
(ξ1 )∫zdz = − |
|
|
f ′′(ξ1 ) , |
|
(6.37) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 t |
( |
t − |
1Уt − 2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H0 = − |
|
∫0 |
|
|
|
|
|
|
|
|
|
|
)( |
) |
dt = |
; |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
где ξ1 [x0 ; x0 |
+ h] и ξ1 |
зависит от h. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
6 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
1 |
= − |
|
1 |
|
∫ |
t |
( |
|
|
|
) |
= |
; |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Далее ∫ R′(z)dz = R(h)− R(0) = R(h), |
|
откуда |
|
с |
учетом |
(6.37) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
t −2 dt |
3 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||
и обобщенной теоремы о среднем имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
2 |
= |
|
4 |
|
∫t(t |
−1)dt = |
6 |
. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
R(h)= |
h |
|
|
|
|
|
|
1 h |
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
3 |
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
′ |
|
|
|
|
|
z |
2 |
′′ |
|
|
|
|
|
|
|
|
|
f |
′′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
∫ |
R (z)dz = |
|
4 |
∫ |
|
|
f (ξ1 )dz = − |
12 |
(ξ), |
|
|
|
|
|
|
Тогда с учетом (6.32) получим на отрезке [x0 ; x2 ]: |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
й |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где ξ1 [x0 ; x0 + h]. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
f (x)dx ≈ (x |
|
|
|
|
|
|
|
|
) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
1 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
− x |
|
|
|
|
|
|
|
H y |
|
= 2h y + y + y , |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
2 |
|
|
|
|
|
|
0 |
|
∑ i |
|
|
|
|
i |
|
|
6 |
|
|
0 |
|
|
3 |
|
1 |
6 |
|
2 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
Таким образом, погрешность метода при интегрировании функ- |
|
|
|
|
x0 |
|
|
|
|
|
|
|
|
|
|
|
i=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
ции на отрезке |
[x0 ; x1 ] по формуле (6.34) имеет величину: |
|
|
р |
|
т.е. |
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ f (x)dx ≈ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
h3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y0 + 4y1 |
+ y2 . |
|
|
|
|
(6.40) |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
′′(ξ), ξ [x0 ; x1 ]. |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
6 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
R = − |
|
|
|
f |
|
|
|
|
|
(6.38) |
|
|
|
|
|
|
x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Геометрически, |
|
в соответствии со смыслом интерполяци- |
|||||||||||||||||||||||||||||||||||||||||||||||||
Из формулы (6.38) видно, что при f |
′′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
(ξ)> 0 формула (6.34) да- |
|
|
|
онной формулы Лагранжа при п = 2, использование формулы |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Rn = |
|
|
|
|
f |
(ξ), |
|
|
|
|
|
|
|
|
′′ |
|
|
|
|
стат |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
ет значение интеграла с избытком, а при f |
|
|
|
|
|
|
- |
|
|
|
(6.40) означает замену подынтегральной функции f(x) парабо- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(ξ)< 0 – с нед |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ком. Можно показать, |
что |
|
при |
|
|
распространении оценки |
(6.38) |
|
|
|
лой L2(x), проходящей через точки Mi(xi, yi) (i = 0, 1, 2). |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
на весь отрезок интегрирования [a;b] получается формула: |
|
о |
|
|
Если считать, что п – четное число (n = 2m), то применяя |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
формулу (6.40) последовательно к каждой паре частичных от- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
h3n |
|
′′ |
|
|
|
|
|
|
|
|
|
|
|
з |
|
|
|
|
|
|
резков [x2i−2 ; x2i ] (i = 1, 2, …, m) получим: |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
12 |
|
|
|
|
|
|
ξ [a;b]. |
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
2h |
y |
|
|
+ y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
С учетом hn =b − a найден следующий окончательный вид |
|
|
|
|
|
∫ f (x)dx ≈ |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
2m |
|
+ 2y1 + y2 +…+ 2y2m−1 . |
|
(6.41) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
a |
|
|
3 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
для оценки погрешности метода интегрир вания по формуле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
трапеций: |
|
|
|
|
|
|
|
|
|
|
п |
|
|
|
|
|
|
|
|
|
|
|
Формула (6.41) называется формулой Симпсона. |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Оценка остаточного члена формулы Симпсона дается формулой: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
Rn |
|
≤ M |
|
b − a |
|
h2 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
е |
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(b − a)h |
|
|
|
|
|
|
|
|
|
v |
(ξ), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
(6.39) |
|
|
|
|
|
|
Rn |
= |
|
|
|
|
|
|
|
f |
′ |
|
ξ |
[a;b]. |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
где |
|
|
|
|
M =max |
f ′′(x) |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
180 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
Р |
x [a,b] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
269 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
270 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||

|
|
|
|
|
|
|
≤ M (b − a)h4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|||||||||||||||||||
|
|
|
|
|
|
R |
, |
|
|
|
|
(6.42) |
|
|
|
Искомый интеграл вычисляется дважды: при делении отрезка |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
n |
|
|
|
|
|
180 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[a;b]. на п частей и на 2п частей (при интегрировании по формуле |
|||||||||||||||||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Симпсона п должно быть четным). Вслед за этим полученные зна- |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
f ′v (x) |
|
|
|
|
|
|
|
|
|
|
|
чения интеграла In и I2n сравниваются, и совпадающие первые деся- |
||||||||||||||||||||||||||||
|
|
|
|
|
|
M = max |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тичные знаки считаются верными. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x [a,b]n |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
Пусть |
Rn и R2n – погрешностиТинтегрирования по |
формуле |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
Как следует из оценки, формула Симпсона, оказывается точной для |
|
|
|
Симпсона, соответственно |
|
при п и 2п отрезках разбиения. Учиты- |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
вая оценку (6.43), можно составить равенство: |
|
||||||||||||||||||||||||||||||||||||||||||||||
полиномов до третьей степени включительно (т.к. для этих случаев |
|
|
|
|
|
А |
|
4 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
производная четвертого порядка равна нулю). Формула Симпсона об- |
|
|
|
|
|
|
|
Rn = hn |
|
|
, |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
ладает повышенной точностью по сравнению с формулой трапеций. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6.44) |
|||||||||||||||||||||||||
|
|
|
|
ГR2n |
4 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
Это означает, что для достижения той же точности, что и по формуле |
|
|
й |
|
|
|
|
h2n |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
трапеций, можно братьменьшее числоотрезковразбиения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
где hn и |
h2n – длина отрезков |
|
|
|
разбиения (шаг интегрирования) |
||||||||||||||||||||||||||||||||||||||||
Укажем простой практический прием позволяющий прогнозиро- |
|
|
|
впервомивторомслучае. Таккак |
h2n = |
|
hn |
, |
тогдаиз(6.44) получаем: |
|||||||||||||||||||||||||||||||||||||||||
вать требуемое число отрезков разбиения по заданной точности ε . |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
и |
Б |
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||||||||||||||||||||||||||||
Пусть задана предельная допустимая погрешность интегрирова- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
ния ε . Желая иметь |
|
R |
|
≤ ε |
с учетом оценки (6.42) достаточно по- |
|
|
|
|
|
R |
n |
=16R |
2n |
. |
|
|
|
|
(6.45) |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
требовать: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
M |
(b − a)h |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
Если I – истинное значение интеграла, то I = In+Rn и I = I2n+R2n , |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
≤ ε, |
|
|
|
|
|
|
|
|
|
откуда In+16R2n= I2n+R2n,, то есть: |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
180 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Откуда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
= |
|
|
In − I2n |
|
|
. |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
h4 ≤ |
|
|
180ε |
|
, т. е. |
|
h ≤ 4 |
|
|
|
|
180ε |
|
|
и |
|
|
|
|
|
|
|
|
2n |
|
|
15 |
|
|
|
|
|
|
|
|
(6.46) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
b − a |
M |
|
|
|
|
|
|
|
|
|
b −a |
|
M |
. |
(6.43) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
Формула (6.46) удобна для практической оценки погрешно- |
||||||||||||||||||||||||||||||||||
Формула (6.43) позволяет оценить величину шага, необходтмую |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
сти метода Симпсона, но требует двойного счета. |
|
||||||||||||||||||||||||||||||||||||||||||||||
для достижения заданной точности. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из оценочных формул (6.39) и (6.42) следует, что ошибка ин- |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тегрирования по методу трапеций и методу Симпсона уменьша- |
|||||||||||||||||||||||||||||||||||
сона возможна лишь тогда, когда |
одынтегральная функция задана |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
биения начинает сильно прогрессировать удельный вес ошибки |
|||||||||||||||||||||||||||||||||||||||||||||||
6.2.9. Оценка точности квадратурных ф рмул |
|
|
|
|
|
|
ется с уменьшением шага интегрирования. При последователь- |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
ном увеличении числа |
отрезков разбиения будем |
получать |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Как следует из оценочных формул (6.38)зи (6.43), оценка по- |
|
|
|
значение интеграла, все более и более близкое к истинному. Этот |
||||||||||||||||||||||||||||||||||||||||||||||
грешности метода интегрирования |
|
ф рмулам трапеций и Симп- |
|
|
|
вывод имеет теоретическое значение. В процессе практических |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
вычислений при последовательном удвоении числа отрезков раз- |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
аналитически. Однако даже и в этом случае на практике применя- |
|
|
|
округления, значение которой с некоторого момента ставит пре- |
||||||||||||||||||||||||||||||||||||||||||||||
ется следующий прием, пригодный для каждого из рассмотренных |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
дел достижимой точности результата интегрирования. |
|
||||||||||||||||||||||||||||||
методов интегрирования. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
271 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
272 |
|
|
|
|
|
|
|
|
|
|
|||||
6.3. Методы решения |
|
|
|
|
|
|
|
|
венная координата. Иначе говоря, в таких уравнениях все функ- |
||||
обыкновенных дифференциальных уравнений |
|
|
|
|
|
ции зависят только от одной переменной и их производные |
|||||||
|
|
|
|
|
|
|
|
|
по этой переменной являются полными. |
|
|||
Инженерные и научные задачи часто связаны с решением диф- |
|
|
|
|
|
|
У |
|
|||||
|
|
|
Уравнения в частных производных содержат более одной не- |
||||||||||
ференциальных уравнений, так как с помощью последних описы- |
|
|
|
зависимой переменной. Этими переменными могут быть, напри- |
|||||||||
ваются многие физические явления. Соответственно, |
процессы |
|
|
|
мер, одновременно пространственные координаты и время или |
||||||||
в технических устройствах так же описываются дифференциаль- |
|
|
|
|
|
Т |
|
||||||
|
|
|
только пространственные координаты для статической задачи. |
||||||||||
ными уравнениями. |
|
|
|
|
|
|
|
|
В таких уравнениях производные от функций по |
любой |
|||
Природа этих процессов различна. При анализе тепловых режи- |
|
|
|
из независимых переменных являются частными. Кроме того, |
|||||||||
мов аппаратуры рассчитывают тепловые потоки, при изучении |
|
|
|
|
А |
|
|
||||||
|
|
|
уравнение может содержать смешанные производные. |
|
|||||||||
электромагнитных процессов – электрические и магнитные поля, |
|
|
|
Г |
|
|
|
||||||
при оценке прочности изделий вычисляют механические напряже- |
|
|
|
|
|
|
|||||||
|
|
|
6.3.1.2. Задача Коши |
|
|
|
|||||||
ния и деформации. |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
К сожалению, для многих практически важных случаев зада- |
|
|
|
Важным элементом задач, содержащих дифференциальные |
|||||||||
чи, описываемые дифференциальными |
уравнениями, весьма |
|
|
|
Б |
|
|
|
|
||||
сложны и получить их точное решение оказывается затрудни- |
|
|
|
уравнения, являются дополнительные условия, которые необходи- |
|||||||||
|
|
|
мы для получения количественного решения. |
|
|||||||||
тельно или невозможно. Эти трудности могут быть связаны с ви- |
|
|
|
Применительно к обыкновенным дифференциальным урав- |
|||||||||
дом уравнения, например, с его нелинейным характером. Однако |
|
|
|
нениям различают два простых вида задач: задачу с началь- |
|||||||||
решить подобные сложные задачи также как и более простые |
|
|
й |
|
|
|
|
||||||
|
и |
ными условиями (задачу Коши) и задачу с краевыми условиями |
|||||||||||
можно с помощью компьютера. Поэтому методы решения диф- |
|
(краевую задачу). |
|
|
|
|
|||||||
ференциальных уравнений на ЭВМ широко применяются в ин- |
|
Задачу Коши можно сформулировать следующим образом. Дано |
|||||||||||
женерной практике. |
|
|
|
|
|
р |
|
обыкновенное дифференциальное уравнение: |
|
||||
6.3.1. Задача Коши и краевая задача |
|
|
|
|
|
|
du(x) |
= f (x,u) |
|
||||
|
|
|
|
|
|
|
|
|
|||||
Методы решения задач, содержащих обыкновенные дифферен- |
|
|
|
|
|
dx |
(6.47) |
||||||
|
|
|
|
|
|
|
|
||||||
циальныения, зависят от их математической формул |
|
о |
|
|
|
|
|
|
|
||||
. Рас- |
|
|
|
|
|
|
|
|
|||||
смотрим их. |
|
|
|
т |
|
|
|
и начальное условие: |
|
|
|
||
6.3.1.1. Классификация уравнений |
ровки |
|
|
|
|
|
|
и(х0 )= и0 . |
(6.48) |
||||
|
|
|
|
Требуется найти функцию и(х), удовлетворяющую уравнению |
|||||||||
|
|
|
|
|
|
|
|||||||
Дифференциальные уравнения принято делить на две группы: |
|
|
|
||||||||||
|
|
|
(6.47) и начальному условию (6.48). |
|
|||||||||
|
|
|
з |
|
|
|
|
|
На практике подобные задачи обычно связаны с расчетом пе- |
||||
обыкновенные дифференциальные уравнения и уравнения в част- |
|
|
|
||||||||||
ных производных. |
|
|
|
|
|
|
|
|
реходных электрических нестационарных тепловых или механи- |
||||
В данном разделе рассматриваютсяметоды решения задач, |
|
|
|
ческих процессов при заданном в некоторый начальный момент |
|||||||||
описываемых обыкнов нными дифф ренциальными уравнения- |
|
|
|
времени исходном состоянии системы. Формулировка краевой |
|||||||||
ми. Эти уравнения сод ржат только одну независимую перемен- |
|
|
|
задачи будет рассмотрена ниже. |
|
||||||||
ную, в качестве которой мож т |
время или пространст- |
|
|
|
|
|
|
|
|
||||
|
|
выступать |
|
|
|
|
|
|
|
|
|
|
|
|
|
273 |
|
|
|
|
|
|
|
|
|
274 |
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
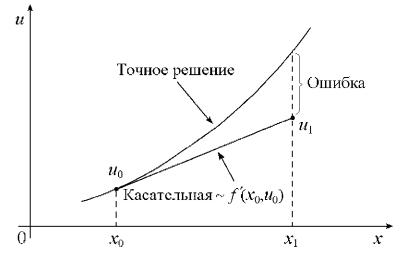
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
6.3.2. Одношаговые методы решения задачи Коши |
|
|
|
|
|
|
|
Т |
|
||||||||||||||||||||
|
|
|
|
|
|
|
u1 = u0 |
+ hf (x0, u0) . |
|
||||||||||||||||||||
К одношаговым относится метод Эйлера (первого порядка), его |
|
|
|
Таким образом (6.50) при известном значении функции u0 = |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
|
|
модификация (второго порядка) и методы Рунге – Кутта (более вы- |
|
|
|
u(x0) в начальной точке x0 позволяет найти приближенное зна- |
|||||||||||||||||||||||||
|
|
|
чение u1 = u(x1) при малом смещении h от x0. На рис. 6.2 гра- |
||||||||||||||||||||||||||
соких порядков). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
фически показан начальный шаг решения методом Эйлера. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
6.3.2.1. Метод Эйлера |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Метод Эйлера является простейшим численным методом реше- |
|
|
|
Б |
|
|
|
|
|||||||||||||||||||||
ния задачи Коши. Рассмотрим его на примере решения обыкновен- |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||
ного дифференциального уравнения первого порядка (6.47) с соот- |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
ветствующим начальным условием (6.48). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Расчетную формулу метода Эйлера можно получить, используя |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
разложение функции и(х) в ряд Тейлора в окрестности некоторой |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
точки хi: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
du(xi ) |
|
|
|
d 2u(xi ) |
|
|
|
|
|
d 3u(xi |
) |
|
|
|
|
|
|
|
|
|
|||
u(x |
|
+ h)= u(x |
)+ h |
+ |
h2 |
|
+ |
h3 |
|
|
+… .(6.49) |
|
|
й |
|
|
|
|
|||||||||||
|
dx |
|
|
dx 2 |
|
|
|
dx 3 |
|
|
|
|
|
|
|
||||||||||||||
|
i |
|
i |
|
|
2! |
|
|
3! |
|
|
|
|
|
|
р |
|
|
|
|
|||||||||
Если приращение h мало (то есть h<<xi), то члены ряда, начиная |
|
|
|
|
|||||||||||||||||||||||||
со слагаемого, включающего h во второй степени, могут быть от- |
|
|
|
|
|
|
|||||||||||||||||||||||
брошены как малые величины. Тогда из (6.49) в первом приближе- |
|
|
|
|
|
|
|||||||||||||||||||||||
нии получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
u(xi |
+ h)= u(xi |
|
)+ h |
du(xi ) |
. |
|
|
(6.50) |
|
|
|
Рис. 6.2. Метод Эйлера |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
Решение можно продолжить, используя найденное значение |
||||||
Воспользуемся формулой (6.50), применив ее к ед нс венной |
|
|
|
||||||||||||||||||||||||||
|
|
|
функции u1 для вычисления следующего значения – u2. Распро- |
||||||||||||||||||||||||||
известной из условия задачи точке x0. Найдем в х0 |
|
|
|
о |
|
|
|||||||||||||||||||||||
про зводную |
|
|
|
страняя эти рассуждения на последующие точки, запишем рас- |
|||||||||||||||||||||||||
du(x0)/dx, подставив (6.48) в (6.47): |
|
|
|
|
з |
т |
|
|
|
четную формулу метода Эйлера в виде: |
|
||||||||||||||||||
|
|
|
du (x0 ) |
|
= f (x0 ,u (x0 )) = f (x0 ,u0 ). и |
|
|
|
|
|
ui+1 = ui + hf (xi, ui), i = 0,1,2,... . |
(6.51) |
|||||||||||||||||
|
|
|
dx |
|
|
|
|
|
|
||||||||||||||||||||
Подставив последнее выражение в (6.50) и п лагая, что xi = x0, |
|
|
|
Из рис. 6.1 видно, что ошибка метода Эйлера на шаге связа- |
|||||||||||||||||||||||||
|
|
|
на с используемой линейной аппроксимацией u(x). Хотя тан- |
||||||||||||||||||||||||||
получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
генс угла наклона касательной к кривой точного |
решения |
||||||||
|
|
u (x0 + h) = u (x0) + hf (x0о, u (x0, u (x0)), |
|
|
|
|
|
|
|
в точке (x0,u0) известен и равен du(x0)/dx, он изменяется при |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
смещении от x0 до xi. Следовательно, при сохранении начально- |
||||
|
|
|
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
го наклона касательной на всем интервале h расчет u1 выполня- |
|||||||
или, сокращая обознач ния, в окончательном виде: |
|
|
|
|
|
|
|
ется с погрешностью. |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
275 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
276 |
|
|
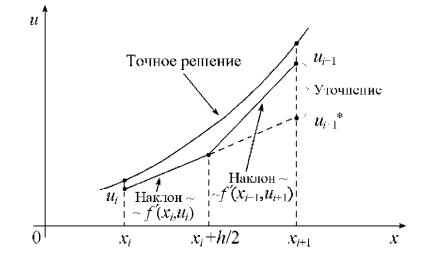
Ошибка метода Эйлера на каждом шаге имеет порядок h2, так |
|
|
|
(6.53) – его коррекцией. Непосредственная подстановка формулы |
|||||||||||||||||||||||||||
как члены, содержащие h во второй и более высоких степенях, от- |
|
|
|
Эйлера (6.51) в правую часть (6.53) дает расчетное соотношение |
|||||||||||||||||||||||||||
брасываются – см. (6.49) и (6.50). Уменьшая h можно снизить ло- |
|
|
|
метода Эйлера - Коши (или метода Хьюна). |
|||||||||||||||||||||||||||
кальную ошибку на шаге. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Графически |
|
|
У |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
модифицированный метод Эйлера представлен |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
на рис. 6.3. Из рисунке видно, что поправка, учитывающая измене- |
|||
6.3.2.2. Модифицированный метод Эйлера |
|
|
|
|
|
|
ние наклона кривой u(x) заметно уменьшает ошибку на шаге h. Мо- |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
Т |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
дифицированный метод Эйлера обеспечивает второй порядок точ- |
|||
Точность метода Эйлера можно существенно повысить, улуч- |
|
|
|
ности. Ошибка на каждом шаге при использовании этого метода |
|||||||||||||||||||||||||||
шив аппроксимацию u(x) на рассчитываемом шаге. Для этого при |
|
|
|
пропорциональна h3. Повышение точности дости гается за счет до- |
|||||||||||||||||||||||||||
разложении u(x) в ряд Тейлора учтем дополнительно слагаемое, со- |
|
|
|
|
А |
|
|||||||||||||||||||||||||
|
|
|
полнительных затрат машинного времени при расчете каждого шага. |
||||||||||||||||||||||||||||
держащее h2 и d2u(xi)/dx2 в (6.49). Определим вторую производную, |
|
|
|
Г |
|
|
|||||||||||||||||||||||||
аппроксимировав ее конечной разностью: |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
Б |
|
|
|
|||||||||||||||||||||
|
d 2u (xi |
) |
|
d du (xi ) |
u′ |
|
u′(xi + h)−u′(xi ) |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
≈ |
|
= |
|
|
|
|
. |
(6.52) |
|
|
|
|
|
|
|||
|
dx2 |
|
|
|
|
|
dx |
|
x |
|
|
h |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
где x = h, u'(xi + h) = du(xi |
+ h)/dx и u'(xi) = du(xi)/dx. |
|
|
|
|
й |
|
|
|
||||||||||||||||||||||
Подставляя полученное выражение в (6.49) и отбрасывая члены |
|
|
|
|
|
||||||||||||||||||||||||||
|
и |
|
|
|
|
||||||||||||||||||||||||||
ряда, начиная со слагаемого, содержащего h3, запишем: |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
du (x ) |
|
|
du (x + h) |
|
|
|
|
|
|
|
||||||
|
u (x |
|
+ h) = u |
(x )+ |
h |
|
|
|
|
р |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
i |
|
+ |
i |
. |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
i |
|
|
|
|
|
|
|
i |
|
|
|
2 |
dx |
|
|
|
dx |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Заменяя в последнем выражении производные так же, как э |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||
было сделано ранее, и используя сокращенные обозначения, полу- |
|
|
|
Рис. 6.3. Модифицированный метод Эйлера |
|||||||||||||||||||||||||||
чим расчетную формулу модифицированного метода Эйлера: |
о |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
h |
( f |
|
(xi ,ui |
)+ f |
|
(xi+1,ui+1 )). |
|
т |
|
|
|
Дальнейшее снижение погрешности решения можно получить |
|||||||||
|
|
|
ui+1 = ui |
+ |
|
|
|
|
|
|
(6.53) |
|
|
|
за счет использования лучшей аппроксимации u(x), учитывающей |
||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
слагаемые высоких порядков. Эта идея положена в основу методов |
|||||
Соотношение (6.53) дает решение для ui+1 в неявномвиде, по- |
|
|
|
||||||||||||||||||||||||||||
|
|
|
Рунге – Кутта. |
|
|
|
|||||||||||||||||||||||||
скольку ui+1 присутствует одновременно в лев й и правой его час- |
|
|
|
|
|
|
|
||||||||||||||||||||||||
тях. Следует отметить, что использ вание неявныхзметодов оправ- |
|
|
|
6.3.2.3. Метод Рунге – Кутта четвертого порядка |
|||||||||||||||||||||||||||
дано тем, что они, как правило, более уст йчивы, чем явные. |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Формула (6.53) может рассматриваться и как явное решение, ес- |
|
|
|
В модифицированном методе Эйлера для получения второй |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
2 |
2 |
|
|
|||
ли в ее правую часть подставить знач ние u*i+1, рассчитав его пред- |
|
|
|
производной d u(xi)/dx используется конечно-разностная формула |
|||||||||||||||||||||||||||
варительно методом Эйл ра |
о формуле (6.51). При этом значение |
|
|
|
(6.52), включающая значения первой производной u'(x) и u'(xi+h) |
||||||||||||||||||||||||||
ui+1* является |
прогнозом, |
а |
|
|
уточн ние результата по формуле |
|
|
|
в начальной и конечной точках шага. Если подобным же образом |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
п |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
277 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
278 |
||||
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
и xi + h. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ψ(h) = u (xi |
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
вычислить третью производную, рассчитав предварительно |
|
|
|
где функция |
+ h) |
− |
ξ(xi , h) |
|
|
показывает |
отклонение |
|||||||||||||||||||||||||
вторую производную в двух точках шага, то можно с помощью |
|
|
|
приближенного |
решения |
ξ(x ,h)от |
точногоu(x + h). |
Увеличение |
||||||||||||||||||||||||||||
(6.49) построить расчетную формулу метода третьего порядка |
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|||||||||
точности. Для этого потребуется определить первую произ- |
|
|
|
параметра p в (6.54) позволяет сделатьУпогрешность, связанную |
||||||||||||||||||||||||||||||||
водную u'(x) в дополнительной промежуточной точке между xi |
|
|
|
с заменой точного решения приближенным, как угодно малой. |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Предположим, что p = 1 . |
|
|
|
, |
|
подставляя (6.54) |
|
в (6.56), |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Аналогичные рассуждения позволяют вывести расчетные фор- |
|
|
|
из условия |
ψ(0) = ψ′(0) = 0 получим A1 = 1 и ψ′′(0) = 0 , откуда: |
|||||||||||||||||||||||||||||||
мулы методов более высоких порядков, обеспечивающих заметное |
|
|
|
u(x + h)≈u(Аx )+ ∑ A k (h)=u + k =u + hf (x ,u ), |
||||||||||||||||||||||||||||||||
снижение погрешности решения. Однако на практике их реализа- |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ция требует существенного повышения объема вычислений с ис- |
|
|
|
|
i |
|
i |
n=1 n n |
|
|
|
|
i |
|
|
|
1 |
|
|
i |
|
i |
i |
|
||||||||||||
пользованием дополнительных промежуточных точек на каж- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
дом шаге. |
|
|
|
|
|
|
|
|
|
|
|
|
что соответствует формуле Эйлера (6.51). Таким же образом можно |
|||||||||||||||||||||||
Существуют и другие способы построения численных методов |
|
|
|
получить формулы более высоких порядков точности, которые на- |
||||||||||||||||||||||||||||||||
с высоким порядком точности. Один из них, применяемый при по- |
|
|
|
зывают методами Рунге – Кутта. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
строении группы методов Рунге – Кутта, заключается в аппро- |
|
|
|
ОднимБиз наиболее известных является вариант метода Рунге – |
||||||||||||||||||||||||||||||||
ксимации решения дифференциального уравнения суммой: |
|
|
|
|
Кутта, соответствующий p = 4. Это метод четвертого порядка точ- |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ности, для которого ошибка на шаге имеет порядок h5. |
|
Его рас- |
|||||||||||||||||||||
|
|
|
|
p |
|
|
|
|
|
|
|
йчетные формулы имеют следующий вид: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
u (xi + h) ≈ ξ(xi ,h) =u (xi )+ ∑Ankn (h), |
|
(6.54) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
n=1 |
|
|
|
|
|
|
и |
|
|
|
|
|
|
k1 + 2k2 + 2k3 + k4 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
о |
|
|
|
ui+1 = ui + |
, |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где An – коэффициенты разложения, kn – последовательность функций: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
k1 = hf (xi ,ui ); |
|
|
|
т(6.55) |
р |
|
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
k1 = hf (xi ,ui ); |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
k2 = hf (xi + α2h, |
|
ui +β21k1 ); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
k3 = hf (xi + α3h, |
ui |
+β31k1 + |
з |
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
k |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
k2 |
= hf xi |
+ |
|
,ui |
|
+ |
|
|
|
; |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||||||||||||||||||
β32k2 ) |
; |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
… |
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||
k3 = hf (xi + α3h, |
ui +β31k1 + |
β32k2 ) |
, |
|
|
|
|
|
|
|
k3 |
= hf xi |
+ |
|
|
,ui |
|
+ |
|
|
|
; |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
п |
|
|
|
|
|
|
|
|
|
|
|
k4 = hf (xi + h,ui |
|
+ k3 ). |
|
|
|
|
|
|
|
||||||||||||||
где αn ,βnm , 0 < m < n <p – некоторые араметры. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
е |
|
выбрать из условия: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Неизвестные параметры An, |
αn ,βnm |
|
|
|
|
Рассмотренные выше метод Эйлера и его модификация |
||||||||||||||||||||||||||||||
|
|
|
|
можно |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Р |
|
|
|
|
|
|
|
|
|
|
|
|
по сути дела являются методами Рунге – Кутта первого и вто- |
|||||||||||||||||||||||
ψ(0) = ψ′(0) = ψ′′(0) =…ψ(K ) (0) = 0, |
(6.56) |
|
|
|
рого порядка соответственно. Несмотря на увеличение объема |
|||||||||||||||||||||||||||||||
|
|
279 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
280 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
