
КП Деревянный каркас одноэтажного производственного здания с13-21
.pdf2.Конструирование и расчет клеефанерной двускатной балки
сплоской стенкой
Двухшарнирная рама является статически неопределимой системой. Преимуществом этой схемы является отсутствие Md в шарнирном соединении ригеля с колонной. Это упрощает конструкцию и дает возможность применения в качестве ригеля клеефанерной двускатной балки. Однако наличие жестких опорных узлов (в основанииколонн) приводит к возникновению опорных моментов,что усложняет конструирование опорных узлов.
2.1Геометрия поперечной рамы
Вкачестве несущих конструкций покрытия приняты клеефанерные балки двускатного очертания. Расчетный пролет балки составляет:
|
|
|
|
|
ld |
= l − 2 0.15 |
= 16 − 2 0.15 = 15.7 |
м |
||||||
В расчетной схеме ригель принимаем прямолинейным. Координаты узлов расчетной схемы |
||||||||||||||
поперечной рамы: |
|
|
|
|
|
|
|
|
|
|
|
|||
- левая опора: X0.left = 0 м, Y0.left |
= 0 м; |
|
|
|
|
|
|
|
||||||
- узел сопряжения левой стойки и ригеля (шарнирный): X1.left = 0 м, Y1.left = H = 6 м; |
||||||||||||||
- правая опора: X0.right = ld = 15.7 |
м, Y0.right |
= 0 м; |
|
|
|
|||||||||
- узел сопряжения правой стойки и ригеля (шарнирный): X1.right = ld |
= 15.7 м, Y1.right = H = 6 м. |
|||||||||||||
|
|
|
|
|
|
2.2 Сбор нагрузок на поперечную раму. |
||||||||
|
|
|
|
|
|
2.2.1 Ветровая нагрузка |
|
|
|
|||||
Нагрузка на вертикальные стойки. |
|
|
|
|
|
|
|
|
|
|||||
Базовое значение скорости ветра (согласно п. 4.2[4]) при: |
|
|
|
|||||||||||
cdir = 1 |
- коэффициент, учитывающий направление ветра; |
|
|
|
||||||||||
cseason = 1 |
- сезонный коэффициент; |
|
|
|
|
|
|
|
||||||
vb.0 = 23 |
|
м |
- основноезначение базовой скорости ветра; |
|
|
|
||||||||
|
с |
м |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
v |
|
= |
c |
c |
season |
v |
b.0 |
= 1 23 = 23 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
b |
|
dir |
|
|
с |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Средняя скорость ветра vm на высоте z над уровнем земли зависит от шероховатости местности,
орографии и базового значения скорости ветра vb.
По табл. 4.1[4] определяем коэффициенты в зависимости от типа местности.
z0 = 0.05 , zij = 0.05 , z = H = 6 м
Коэффициент местности по формуле (4.5) [4]:
z0 0.07 |
|
0.05 |
|
0.07 |
||||||||
kr = 0.19 |
|
|
|
|
= 0.19 |
|
|
|
|
|
= 0.19 |
|
|
|
|
0.05 |
|
||||||||
zij |
|
|
|
|||||||||
Коэффициент, учитывающий тип местности: |
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
6 |
|
|||||||
cr = kr ln |
|
|
|
= |
0.19 ln |
|
|
|
|
|
= 0.91 |
|
|
|
|
|
|
|
|
||||||
z0 |
|
|
0.05 |
|
||||||||
13
Орографический коэффициент согласно п.4.3.3 [4] |
c0 = 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
vm = cr c0 vb = |
0.91 23 = 20.921 |
|
м |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
с |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Интенсивность турбулентности при коэффициенте турбулентности |
|
kt = 1 |
|
|
|
|
|||||||||||||||||||||
|
|
|
lv = |
|
|
kt |
|
|
= |
|
1 |
|
= |
0.209 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
c0 ln |
|
|
|
|
ln |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
z0 |
|
|
|
0.05 |
|
|
|
|
|
|
|
|
|
|||||
Пиковое значение скоростного напора согласно п.4.5 [4] ( |
z = 6 м ) |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
(при плотности воздуха |
ρв |
= 1.25 |
|
|
кг |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
м3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
qp = (1 |
+ 7 lv) |
1 |
ρв |
2 |
|
− 3 |
|
|
|
+ 7 0.209) |
1 |
|
|
|
|
2 |
|
− 3 |
= 0.674 кПа |
||||||||
|
vm |
10 |
|
|
= |
(1 |
|
1.25 20.921 |
|
10 |
|
||||||||||||||||
2 |
|
|
2 |
|
|
||||||||||||||||||||||
Коэффициенты внешнего давления для вертикальных стен согласно табл. 7.1 [4]: |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
cpe.D = 0.717 |
|
|
cpe.E = −0.5 |
|
|
|
|
|
|
|
|
|||||||||||
Внешнее ветровое давление с наветренной стороны (зона D) по формуле (5.1) [4]:
we.D = qp cpe.D = 0.674 0.717 = 0.483 кПа
Внешнее ветровое давление с подветренной стороны (зона Е) по формуле (5.1) [4]:
we.E = qp cpe.E = 0.674 −0.5 = −0.337 кПа
Эквивалентная равномерно распределенная нагрузка на раму с наветренной стороны:
qw.D = we.D B γQ = |
0.483 4.1 1.5 = 2.969 |
кН |
м |
Эквивалентная равномерно распределенная нагрузка на раму с подветренной стороны:
qw.E = we.E B γQ = |
−0.337 4.1 1.5 = −2.071 |
кН |
м |
2.2.2 Снеговая нагрузка
Коэффициент формы снеговых нагрузок, которые должны использоваться для двускатных покрытий, при отсутствии снегоудерживающих заграждений при уклоне менее 30 градусов:
μi = 0.8
Согласно рис. 5.6 [4] следует рассматривать 2 схемы распределения снеговой нагрузки - случай 1 и случай 2:
14
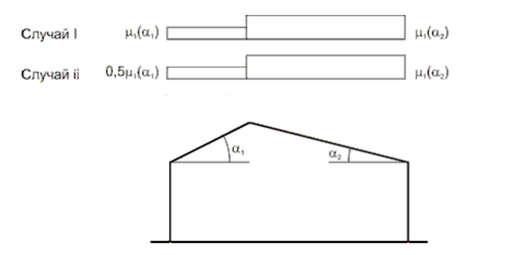
Рис. 2.3 - Схемы распределения снеговой нагрузки согласно [4]
Характеристическое значение снеговой нагрузки:
sk |
= 1.45 + 0.6 |
(A − 150) |
= 1.45 + 0.6 |
186 − 150 |
= 1.666 кПа |
|
|
||||
|
100 |
100 |
|
||
Нормативное значение снеговой нагрузки для случая 1:
sn1 = μi Ce Ct sk = 0.8 1.666 = 1.333 кПа
Нормативные значения снеговой нагрузки для случая 2 (для левого и правого полупролетов):
sn2.left = 0.5 μi Ce Ct sk = 0.5 0.8 1.666 = 0.666 кПа sn2.right = μi Ce Ct sk = 0.8 1.666 = 1.333 кПа
Расчетное значение снеговой нагрузки для случая 1:
s1d = sn1 γq = 1.333 1.5 = 1.999 кПа
Расчетные значения снеговой нагрузки для случая 2 (левый и правый полупролеты):
s2d.left = sn2.left γq = 0.666 1.5 = 1 кПа s2d.right = sn2.right γq = 1.333 1.5 = 1.999 кПа
Коэффициент, учитывающий уклон полупролета балки:
k = cos |
|
α |
|
π = 0.995 |
||||||
|
|
|||||||||
180 |
|
|||||||||
Снеговая нагрузка,приведенная к 1 п.м. |
|
|
|
|
|
|
|
|
||
- расчетная для случая 1: |
|
|
|
|
|
|
кН |
|||
qs.d1 = s1d B k |
= |
|
1.999 4.1 0.995 = 8.152 |
|||||||
|
м |
|||||||||
|
|
|
|
|
|
|
|
|||
- расчетная для случая 2 (левый и правый полупролеты): |
|
|
|
|
|
|
|
|
||
qs.d2.left = s2d.left B k = 1 4.1 0.995 = 4.076 |
кН |
|
||||||||
м |
||||||||||
|
|
|
|
|
||||||
qs.d2.right = s2d.right B k |
= |
1.999 4.1 0.995 = 8.152 |
кН |
|||||||
м |
|
|||||||||
2.2.3Постоянные нагрузки
Кпостоянным нагрузкам относятся собсвенный вес балки и колонны и вышележащих конструкций.
Нагрузку от кровли и плит берем из таблицы сбора нагрузок на плиту покрытия. Нормативный собственный вес балки определяется по формуле (1.1) [1]:
15
|
|
|
g2k |
= |
q1k |
+ qs.k |
0.24 + 1.333 |
= 0.153 кПа |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
1000 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
1000 |
|
− 1 |
|
− 1 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
kswl |
5.55616 |
|
|
|
||||||||||||
где q1k - постоянная нормативная нагрузка от покрытия; |
|
|
|
|
|
|
|
|
||||||||||||||||||
qs.k |
- полное нормативное значение снеговой нагрузки; |
|
|
|
|
|
|
|||||||||||||||||||
ksw |
- коэффициент собственного веса конструкции, принимаемый по табл. 1.6 [1]; |
|||||||||||||||||||||||||
l - расчетный пролет рамы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Расчетное значение собственного веса балки: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
g2d = g2k γf = 0.1531.35 = 0.207 |
кПа |
||||||||||||||||||||
Нормативное значение собственного веса колонны: |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
g2k1 = |
q1k + qs.k |
0.24 + 1.333 |
= 0.137 кПа |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
1000 |
− 1 |
|
1000 |
|
|
− 1 |
|
|
|
|
|
|
||||||||||||
|
|
|
kswl |
|
|
|
516 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Расчетное значение собственного веса колонны (на 1.м.п): |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
q2d.l = g2k1 B |
l |
|
1.35 |
= |
0.137 4.1 |
16 |
|
1.35 |
= 1.009 |
кН/м |
|||||||||||||||
|
|
|
|
|
||||||||||||||||||||||
|
2 |
|
|
H |
|
|
|
|
|
|
|
2 |
6 |
|
|
|
|
|||||||||
Нагрузки, действующие на поперечную раму, приведены в таблице 2.1.
Таблица 2.1 Нагрузки на раму
Вид нагрузки |
Нормат, кПа |
Расчетная qd, кПа |
k |
|
qd*k |
Погонная, кН/м |
|
Постоянная: |
|
|
|
|
|
|
|
Кровля+плиты покрытия |
0,24 |
0,324 |
- |
|
- |
1,328 |
|
Собственный вес балки |
0,153 |
0,2 |
|
0,995 |
0,199 |
0,816 |
|
Собственный вес колонны |
0,137 |
0,18495 |
- |
|
- |
1,009 |
|
Итого постоянная (покрытие): |
|
|
|
|
2,144 |
||
Снеговая : |
|
|
|
|
|
|
|
1) |
по первому варианту |
1,333 |
1,999 |
|
0,995 |
1,989 |
8,152 |
2) |
по второму варианту |
0,6665 |
0,9995 |
|
0,995 |
0,995 |
4,076 |
2.3 Статический расчет поперечной рамы
Статический расчет рамы выполняем в программном комплексе "Raduga". Из загружений сформированы следующие расчетные комбинации:
1)Постоянная + снеговая по первому варианту;
2)Постоянная + снеговая по второму варианту;
3)Постоянная + снеговая по второму варианту + ветровая. В данном случае ветровая нагрузка входит в сочетание с коэффициентом 0.6.
16
Сопряжение полуригеляи стойки принято шарнирное,стоек с фундаментом - жесткое. При формировании комбинаций загружений справедлив принцип независимости действия сил. Эффект от суммарного воздействия равен сумме эффектов от каждого из воздействий.
При подборе сечений - карнизного, опорного и в конькеиспользуются результаты статического расчета рамы по соответствующей, наиболее неблагоприятной для работы рассматриваемого элемента комбинации нагружений.
Расчет выполнен методом конечных элементов. Тип используемых конечных элементов - стержень. Нумерация узлов и стержней, загружения а также эпюры внутренних усилий представлены в Приложении А.
2.4 Конструирование двускатной клеефанерной балки
Пояса изготовлены из досок размером 200х40 мм. После фрезерования доски будут иметь
размеры hf = 200 − 10 = 190 мм, h1 = 40 − 6 = 34 |
мм. Ширина поясов bf |
= 6 h1 = 6 34 = 204 |
мм |
||||||||||||||||||||
без учета толщины стенки. Толщину фанерной стенки принимаем равной tw = 15 мм. |
|
||||||||||||||||||||||
Высоту балки на опоре рекомендуется принимать равной hs |
= |
103 |
16 = 640 мм |
|
|
||||||||||||||||||
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25 |
|
|
|
|
|
|
|
||
Высота сечения на опоре hs = 700мм. Высоту балки в середине пролета рекомендуется |
|
||||||||||||||||||||||
принимать hap = |
|
103 |
16 |
= 1454.545 мм. Принимаем hap = 1500мм. |
|
|
|
||||||||||||||||
11 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Угол уклона верхней кромки балки: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
hap − hs |
|
180 |
|
|
1500 − 700 |
|
180 |
|
o |
|
|
||||||||
|
|
α = atan |
|
|
|
= |
atan |
|
|
|
|
|
|
|
|
|
= 5.819 |
|
|
||||
|
|
|
π |
|
|
|
|
|
π |
|
|
||||||||||||
|
|
|
|
0.5 ld 103 |
|
|
|
0.5 15.7 103 |
|
|
|
|
|
||||||||||
2.4.1 Определение механических характеристик клееной древесины |
|
||||||||||||||||||||||
Характеристические значения сопротивления клееной древесины определяются на |
|
||||||||||||||||||||||
основании соответствующих значений отдельных слоев согласно таблице А1 СТБ EN |
|
||||||||||||||||||||||
1194-2011: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- прочность при изгибе: fm.g.k = 7 + 1.15 ft.0.k |
= 7 + 1.15 16 = 25.4 |
МПа; |
|
|
|
||||||||||||||||||
- прочность при растяжении вдоль волокон: ft.0.g.k |
= 5 + 0.8 ft.0.k |
= |
5 + 0.8 16 = 17.8 МПа; |
|
|||||||||||||||||||
- прочность при растяжении поперек волокон: ft.90.g.k = 0.2 + 0.015 ft.0.k |
= 0.2 + 0.015 16 = 0.44 |
М |
|||||||||||||||||||||
Па; |
|
|
|
|
|
|
|
= 7.2 (ft.0.k )0.45 = |
7.2 16 0.45 = 25.072 |
|
|
||||||||||||
- прочность при сжатии вдоль волокон: fc.0.g.k |
МПа; |
|
|||||||||||||||||||||
- прочность при сжатии поперек волокон: fc.90.g.k |
= |
0.7 (ft.0.k )0.5 |
= |
0.7 16 0.5 = 2.8 |
МПа; |
|
|||||||||||||||||
- прочность при скалывании: fv.g.k = 0.32 ft.0.k |
0.8 |
= |
0.32 16 0.8 = 2.941 МПа; |
|
|
||||||||||||||||||
- модуль упругости: E0.g.mean = 1.05 Emean |
= |
1.05 11000 |
= 11550 |
МПа; |
|
|
|
||||||||||||||||
E0.g.05 = 0.85 Emean = 0.85 11000 |
= 9350 |
МПа; |
|
|
|
|
|
|
|
|
|||||||||||||
E90.g.mean |
= 0.035 Emean |
= |
0.035 11000 |
= 385 |
МПа; |
|
|
|
|
|
|
||||||||||||
- модуль сдвига: |
Gg.mean |
= 0.065 Emean |
= |
0.065 11000 |
= 715 |
МПа; |
|
|
|
|
|
|
|
||||||||||
- плотность: ρg.k |
= 1.1 ρk |
= 1.1 370 = 407 |
кг/м3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Расчетные значения сопротивления клееной древесины:
17
- прочность при изгибе для сечения всередине пролета балки:
|
|
kmod ksys kh fm.g.k |
|
0.8 25.4 |
МПа; |
||
fm.g.d.ap |
= |
|
= |
|
= 16.256 |
||
γM |
1.25 |
||||||
|
|
|
|
|
|||
где kmod = 0.8 , ksys = 1 , kh = 1 |
, γM = 1.25 |
|
|
|
|
||
- прочность при растяжении клееной древесины поперек волокон:
|
|
kmod ksys ft.0.g.k |
0.8 |
17.8 |
МПа; |
||
ft.0.g.d |
= |
|
= |
|
|
= 11.392 |
|
γM |
|
|
|||||
|
|
1.25 |
|
|
|||
- прочность при сжатии клееной древесины поперекволокон:
|
|
kmod ksys fc.0.g.k |
|
0.8 25.072 |
МПа; |
||
fc.0.g.d |
= |
|
= |
|
= 16.046 |
||
γM |
1.25 |
||||||
|
|
|
|
|
|||
- прочность клееной древесины при сдвиге:
|
|
kmod ksys fv.g.k |
|
0.8 2.941 |
МПа. |
||
fv.g.d |
= |
|
= |
|
= 1.882 |
||
γM |
1.25 |
||||||
|
|
|
|
|
|||
Характеристические значения сопротивления фанеры (стенки балки) при γM = 1:
- прочность материала стенки при сжатии фанеры вдоль волокон: = 36 МПа
- прочность материала стенки при растяжении фанеры вдоль волокон: = 36 МПа
- прочность материала стенки на скалывание вдоль оси балки:
fv.0.k = 9.5 МПа
- прочность материала стенки на скалывание вдоль оси балки:
fv.90.k = 9.5 МПа
Расчетные значения сопротивления фанеры стенки балки:
- прочность материала стенки при сжатии фанеры вдоль волокон:
fw.c.d |
= |
kmod ksys fw.c.k |
= |
0.8 |
36 |
= 28.8 |
МПа |
γM |
1 |
|
|||||
|
|
|
|
|
|
- прочность материала стенки при растяжении фанеры вдоль волокон:
fw.t.d |
= |
kmod ksys fw.t.k |
= |
0.8 |
36 |
= 28.8 |
МПа |
γM |
1 |
|
|||||
|
|
|
|
|
|
- прочность материала стенки на скалывание вдоль оси балки:
|
|
kmod ksys fv.0.k |
|
0.8 9.5 |
МПа |
||
fv.0.d |
= |
|
= |
|
= 7.6 |
||
γM |
1 |
||||||
|
|
|
|
|
|||
- прочность материала стенки на скалывание вдоль оси балки:
|
|
kmod ksys fv.90.k |
|
0.8 9.5 |
МПа |
||
fv.90.d |
= |
|
= |
|
= 7.6 |
||
γM |
1 |
||||||
|
|
|
|
|
|||
2.4.2 Расчет клеефанерной балки по предельным состояниям несущей способности
Вследствие того, что в составном сечении балки материалы имеют неодинаковые значения ползучести, напряжения изгиба по сечению будут зависеть от продолжительности действия нагрузки и влажности. В связи с этим в расчетах необходимоучитывать распределение напряжений в сечении балки как для начального состояния (inst) после непосредственного нагружения, так и для конечного состояния (fin) с учетом продолжительности действия нагрузки. Прежде чем вычислять напряжения в характерных точках сечения, вычислим необходимые геометрические характеристики сечения. Значение момента в коньке балки: MEd = 317.05 кНм
18
Момент инерции стенки балки относительно нейтральной оси (в середине пролета балки):
|
t |
w |
h |
3 |
|
15 |
1500 |
3 |
4 |
I = |
|
|
w |
= |
|
= 4218750000 мм |
|||
|
|
|
|
|
|
|
|||
w |
12 |
|
|
12 |
|
|
|||
|
|
|
|
|
|
||||
Момент инерции сечения поясов относительно нейтральной оси:
|
|
|
h |
3 |
h |
|
− h |
|
2 |
|
|
|
|
|
3 |
|
|
||||
|
b |
f |
f |
ap |
f |
|
|
|
|
204 190 |
|
+ |
1500 |
− 190 |
|||||||
I |
= |
|
|
+ |
|
|
|
b |
f |
h 2 |
= |
|
|||||||||
|
|
|
|
|
|
|
2 |
|
12 |
|
|
2 |
|||||||||
f |
12 |
|
|
|
|
|
|
|
f |
|
|
|
|||||||||
2 |
|
4 |
|
204 190 2 = 33491224000 |
мм |
Момент инерции поперечного сечения балки, приведенный к материалу поясов, мм4:
|
|
|
|
|
|
Ew.mean |
|
5500 |
|
|
|
|
|
|||||
|
I |
= I |
+ |
|
|
|
I = |
33491224000 + |
|
|
|
|
4218750000 = 35500152571.429 |
|||||
|
|
|
|
|
|
|||||||||||||
|
ef.inst |
f |
|
|
|
|
|
w |
|
11550 |
|
|
|
|
|
|||
|
|
|
|
|
|
Ef.mean |
|
|
|
|
|
|
||||||
|
|
Ew.mean |
1 |
+ kdef.f |
|
5500 |
|
|
1 + 0.8 |
|
||||||||
Ief.fin = If |
+ |
|
|
|
|
|
|
|
Iw = 33491224000 |
+ |
|
|
|
|
|
4218750000 = 35299259714.286 |
||
Ef.mean |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
1 |
+ kdef.w |
|
11550 |
|
1 + 1 |
|
|||||||||
Статический момент площади пояса балкиотносительно нейтральной оси у опоры балки (без учета стенки):
Sf |
= bf hf |
|
hs − hf |
= 204 190 |
700 − 190 |
= 9883800 мм3 |
|
|
|||||
|
|
2 |
2 |
|
||
Максимальные расчетные значения сжимающих напряжений в поясе балки для начального состояния (inst):
σf.inst.c.max.d |
= |
MEd 106 |
|
hap |
|
= |
|
317.05 |
10 |
6 |
|
1500 |
= |
6.736 |
МПа |
Ief.fin |
|
|
35299259714.286 |
2 |
|||||||||||
|
|
2 |
|
|
|
|
|
|
|||||||
σf.inst.c.max.d = 6.736 |
|
< fm.g.d.ap |
= |
16.256 МПа |
|
|
|||||||||
Максимальные расчетные значения сжимающих напряжений в поясе балки для начального состояния (inst):
σf.inst.t.max.d |
|
MEd 106 |
hap |
|
317.05 106 |
1500 |
|
МПа |
||||
= |
|
|
|
|
= |
|
|
|
|
= 6.736 |
||
Ief.fin |
|
2 |
35299259714.286 |
2 |
||||||||
|
|
|
|
|
|
|
|
|||||
σf.inst.c.max.d |
= |
6.736 |
< ft.0.g.d = 11.392 |
МПа |
|
|||||||
Расчетные значения сжимающих напряжений в поясе балки (средние):
σf.inst.c.d |
|
MEd 106 |
hap |
− hf |
|
317.05 106 |
1500 − 190 |
|
||||
= |
|
|
|
|
= |
|
|
|
|
= 5.85 |
МПа |
|
Ief.inst |
|
2 |
35500152571.429 |
2 |
||||||||
|
|
|
|
|
|
|
|
|||||
σf.inst.c.d = 5.85 |
< kc.z fc.0.g.d |
= 0.949 16.046 |
= 15.229 МПа |
|
||||||||
где kc.z - коэффициент продольного изгиба,определяют по формуле:
|
|
|
kc.z = |
|
|
|
|
1 |
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
= 0.949 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
kz + |
|
kz |
2 + λrel.z |
2 |
0.511 + |
0.511 2 + 0.183 2 |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
λz |
|
|
|
|
fc.0.k |
|
|
|
|
11.855 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
λrel.z |
= |
|
|
|
|
|
= |
|
|
22 |
|
= 0.183 |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
E0.g.05 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
π |
9350 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
l |
|
|
103 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
2 bf hf |
|
|
|
|
|
|
16 |
|
10 |
|
|
|
|
|||||||||||||||||||||
|
|
|
λz |
= |
|
= |
|
|
|
2 204 190 |
= 11.822 |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
2 |
Ief.inst |
2 |
35500152571.429 |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
kz = 0.5 |
|
|
+ βc (λrel.z |
|
|
|
|
|
|
|
|
|
|
|
2 |
= |
|
|
|
+ 0.1 (0.183 − 0.3) + 0.183 |
2 |
= 0.511 |
|||||||||||||||||
1 |
− 0.3) + λrel.z |
0.5 1 |
|
||||||||||||||||||||||||||||||||||||
19
При симметричном сечении σf.inst.t.d = σf.inst.c.d = 5.85 МПа < ft.0.g.d = 11.392 МПа.
Проверим расчетные напряжения в поясах балки для конечного состояния (fin):
σf.fin.c.max.d = |
MEd 106 |
|
hap |
|
|
|
317.05 106 |
|
|
|
|
1500 |
= 6.736 МПа |
||||||||||
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
||||||
|
|
Ief.fin |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
2 |
|
35299259714.286 |
|
|
2 |
|
|
|||||||||||
|
|
σf.fin.c.max.d = 6.736 |
|
< fm.g.d.ap = 16.256 МПа |
|
||||||||||||||||||
|
σf.fin.t.max.d = σf.fin.c.max.d |
= 6.736 < fm.g.d.ap |
= 16.256 |
МПа |
|||||||||||||||||||
σf.fin.c.d |
|
MEd 106 |
hap − hf |
|
|
|
317.05 106 |
|
|
1500 − 190 |
|
||||||||||||
= |
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
= 5.883 МПа |
|||
Ief.fin |
|
2 |
|
|
35299259714.286 |
|
2 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
σf.fin.c.d = 5.883 |
< kc.z fc.0.g.d |
= 0.949 16.046 |
= 15.229 |
МПа |
||||||||||||||||||
|
|
σf.fin.t.d |
= σf.fin.c.d = 5.883 |
< ft.0.g.d |
= 11.392 |
МПа |
|||||||||||||||||
Максимальные напряжения от изгиба возникают в крайних кромках стенки, их следует определять как для поясов в начальном состоянии (inst) и в конечном состоянии (fin) с учетом продолжительности действия нагрузки.
|
σw.inst.c.d |
|
|
MEd |
106 |
hap |
Ew.mean |
|
|
317.05 106 |
|
|
1500 |
|
|
5500 |
|
= 3.19 МПа |
|
|||||||||||
|
= |
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
2 |
|
35500152571.429 |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
Ief.inst |
|
Ef.mean |
|
2 11550 |
|
|
|
|
|||||||||||||||||
|
|
MEd 106 |
|
|
|
|
|
σw.inst.c.d = 3.19 |
< fw.c.d = 28.8 |
МПа |
|
|
|
|
|
|
||||||||||||||
σw.fin.c.d |
|
hap |
|
Ew.mean (1 + kdef.f ) |
|
|
317.05 106 |
|
|
1500 |
5500 |
(1 + 0.8) |
МПа |
|||||||||||||||||
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
= 2.887 |
||||||
Ief.fin |
|
2 |
|
Ef.mean (1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
+ kdef.w) |
35299259714.286 |
2 |
|
|
|
11550 (1 + 1) |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
σw.fin.c.d = 2.887 |
< fw.c.d = 28.8 |
МПа |
|
|
|
|
|
|
||||||||||||||
σw.inst.t.d := σw.inst.c.d |
= 3.19 |
< fw.t.d |
||||
σw.fin.t.d |
:= σw.fin.c.d = 2.887 |
< fw.t.d |
||||
Проверка устойчивостистенки. |
|
|
|
|
|
|
|
hf |
|
− 3 = 15 700 1 + |
|||
Fv.w.Ed = tw hw 1 + |
|
|
fv.0.d 10 |
|||
|
||||||
|
hw |
|
|
|
|
|
Значение поперечной силы у опоры балки: |
|
= 80.78 кН |
||||
|
|
|
VEd |
|
||
=28.8 МПа
=28.8 МПа
190 |
7.6 10− 3 = 101.46 кН |
|
700 |
||
|
Проверим условие устойчивости стенки балки:
VEd = 80.78 < Fv.w.Ed = 101.46 кН
Условие выполняется. Устойчивость стенки обеспечена. Проверка клеевых швов на скалывание:
2 tw 0.8 |
|
2 15 |
|
0.8 |
||||
τmean.d = fv.0.d |
|
|
= 7.6 |
|
|
|
= 1.736 МПа |
|
hf |
190 |
|
||||||
|
|
|
|
|||||
Напряжения, возникающие в клеевых швах от действия расчетной поперечной силы:
τmean |
|
VEd |
Sf 103 |
80.78 9883800 103 |
||
= |
|
|
= |
|
= 0.059 МПа |
|
|
|
|
||||
|
|
2Ief.inst hf |
2 35500152571.429 190 |
|||
|
τmean = 0.059 |
< τmean.d = 1.736 МПа |
||||
Поскольку все проверки выполняются, то немущая способность балки обеспечена.
20
2.4.3 Расчет клеефанерной балки по предельным состояниям эксплуатационной пригодности
Начальный прогиб балки без учета влияния переменности высоты сечения и деформаций сдвига, определяют в зависимости от типа балки, схемы опирания и закона распределения нагрузки по длине рассчитываемого элемента. В данном случае (согласно таблице 8.2 [2] при шарнирном опирании балки и равномерно распределенной нагрузке по ее длине (qk = 7.02 кН/м):
|
5 |
|
qk ld |
4 1012 |
|
5 |
|
7.02 15.7 4 1012 |
||
u0 |
= |
|
|
|
|
= |
|
|
|
= 13.544 мм |
|
E0.g.mean Ief.inst |
|
|
|||||||
|
384 |
|
|
384 |
|
11550 35500152571.429 |
||||
Перед вычислением начального прогиба uinst найдем значения коэффициентов (табл.8.3[2]):
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β = |
|
hs |
|
= |
700 |
|
|
= 0.467 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
hap |
|
|
1500 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kh1 |
= 0.4 + 0.6 β |
= |
|
0.4 + 0.6 0.467 |
= 0.68 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
kv = |
|
(2.26 |
− 0.35 β) (hap − 2hf ) tw |
|
|
= |
|
(2.26 − 0.35 0.467 ) (1500 |
− 2 190) 15 |
|
= 0.454 |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 204 190 |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2bf hf |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Начальный прогиб дощатоклееной балки с учетом переменности высоты сечения: |
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
u |
0 |
|
|
|
|
|
h |
ap |
2 |
E |
|
|
|
|
|
13.544 |
|
|
|
|
1500 |
|
|
|
2 |
11550 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0.g.mean |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
u |
|
= |
|
|
|
|
1 + |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
1 + 0.454 |
|
|
|
|
|
|
|
|
|
|
= 21.253 |
мм |
||||
inst |
k |
|
|
|
v |
|
|
|
|
G |
|
|
|
0.68 |
|
|
3 |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
715 |
|
|
||||||||||||||||||||||
|
|
|
|
h1 |
|
|
ld 10 |
|
|
|
g.mean |
|
|
|
|
|
|
|
|
|
|
|
15.7 10 |
|
|
|
|
|
|
|
|
||||||||||||||
Предельное значение uinst для балки как элемента покрытия согласно таблице 8.1[2] составляет |
|
||||||||||||||||||||||||||||||||||||||||||||
1/400 пролета. Проверяем выполнение условия: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
uinst |
= 21.253 |
мм < |
|
1 |
|
|
ld |
|
103 = |
|
1 |
15.7 103 = 39.25 |
мм |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
400 |
|
|
|
||||||||||||||||||||||||||||
Условие выполняется. |
|
|
|
|
|
|
|
|
|
400 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Значение полного прогиба: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
ufin = uinst (1 + kdef ) |
= |
|
|
21.253 (1 + 0.8) |
= 38.255 |
|
мм |
|
|
|
|
|
||||||||||||||||||||||
Согласно таблице 8.1[2] предельное значение полного прогиба для балки как элемента покрытия составляет не более 1/300 пролета. Проверяем условие:
ufin |
= 38.255 мм < |
1 |
ld 103 = |
1 |
15.7 103 = 52.333 мм |
|
300 |
||||
|
300 |
|
|
||
Условие выполняется. Значениепрогиба непревышает предельно допустимое значение. Поскольку все необходимые проверки выполняются, дощатоклееная балка запроектирована верно.
21
