3 курс / Фармакология / Миронов_А_Н_,_Бунатян_Н_Д_и_др_Руководство_по_проведению_доклинических

Средняя разность равна

Ошибка разности

Критерий t=d/Sd = 4,1/0,31 = 13,4. Для уровня значимости 5 % и числа степеней свободы f=10–1=9 критическое значение равно (таблица 1) 2,26. Так как вычисленное значение критерия превышает соответствующее табличное, нулевую гипотезу отвергают и с вероятностью более 95 % можно утверждать, что разница между средними значениями сравниваемых выборок статистически достоверна.

Правильное применение t-критерия предполагает нормальное распределение совокупностей, из которых извлечены сравниваемые выборки. Если это условие не выполняется, то более эффективными будут непараметрические критерии.

6.Непараметрические критерии для проверки гипотез

оразличии (сходстве) между двумя параллельными группами

ио значимости изменений показателя (парные сравнения)

Как уже говорилось выше, литературные данные из области экспериментальной биологии свидетельствуют о том, что распределение животных одного и того же вида по их чувствительности к воздействию лекарственного препарата достаточно хорошо описывается нормальным законом распределения. А значит, обычно изучаемые параметры фармакологического эффекта при их представлении в количественной форме могут анализироваться в рамках параметрического подхода. Однако при количественной форме описания признаков для их сравнения может применяться и целый ряд непараметрических критериев (особенно в случае малых объемов выборок) среди которых важное место занимают так называемые ранговые критерии. Применение этих критериев основано на ранжировании членов сравниваемых групп. При этом сравниваются не сами члены ранжированного ряда, а их порядковые номера или ранги. Познакомиться с основными непараметрическими критериями — X-критерием Ван-дер-Вардена (для независимых выборок), U-критерием Уилкоксона (для независимых выборок), критерием знаков z (для попарно связанных выборок), T-критерием Уилкоксона (для попарно связанных выборок) — можно, например, в книгах [6, 7, 9, 12, 13, 17, 19]. Там же даны и основные таблицы для проверки этих критериев. При решении конкретной задачи очень важно правильно выбрать критерий, решение этих вопросов для медико-биологических приложений достаточно подробно рассмотрено в [4, 9, 17, 19].

Приведем U-критерий Уилкоксона (Манна-Уитни) для проверки гипотезы о принадлежности сравниваемых независимых выборок к одной и той же генеральной совокупности или совокупностям с одинаковыми параметрами. Гипотезу проверяют, расположив в обобщенный ряд значения сравниваемых выборок в возрастающем порядке. Всем значениям полученного обобщенного ряда присваиваются ранги от 1 до N=n1+n2. Для каждой выборки находятся суммы рангов R и рассчитываются статистики:

Если нулевая гипотеза верна и выборки извлечены из одной и той же генеральной совокупности, мы не должны ожидать преобладания наблюдений из одной выборки на одном из концов объединенного вариационного ряда, их значения должны быть достаточно равномерно рассеяны по всему обобщенному ряду. Таким образом, слишком большие или слишком маленькие значения статистики R должны заставить нас усомниться в справедливости нулевой гипотезы.

Вкачестве тестовой статистики выбирают минимальную величину U и сравнивают ее

стабличным значением для принятого уровня значимости. Гипотеза принимается и раз-

901

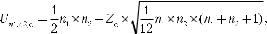
личия считаются недостоверными, если рассчитанное значение больше соответствующего табличного (таблица 4).

Обычно в таблицах приводятся критические значения данного критерия для объема выборок 20 или 40. В случае выборок большего объема для проверки данного критерия применяется нормальная аппроксимация. Тогда критические значения для критерия U можно рассчитать по формуле:

где Zα — критические значения стандартного нормального распределения (таблица 7).

Пример 6.

Проверим гипотезу о принадлежности сравниваемых независимых выборок к одной и той же генеральной совокупности с помощью непараметрического U-критерия Уилкоксона. Сравним результаты, полученные в примере 4 для 2 и 3-го столбцов таблицы 11 по критерию Стьюдента, с результатами непараметрического сравнения. Для расчета U-критерия Уилкоксона расположим варианты сравниваемых выборок в порядке возрастания в один обобщенный ряд и присвоим вариантам обобщенного ряда ранги от 1 до n1+n2. Первая строка представляет собой варианты первой выборки, вторая — второй выборки, третья — соответствующие ранги в обобщенном ряду:

6 7 7 8 8 9 9 9 10 11

89 9 11 11 12 12 12 13 13

1 2,5 2,5 5 5 5 9 9 9 9 9 12 14 14 14 17 17 17 19,5 19,5 Надо обратить внимание, что если имеются одинаковые варианты, им присваивается

средний ранг, однако значение последнего ранга должно быть равно n1+n2 (в нашем случае 20). Это правило используют для проверки правильности ранжирования.

Отдельно для каждой выборки рассчитаем суммы рангов их вариант R1 и R2. В нашем случае

R1=1+2,5+2,5+5+5+9+9+9+12+14=69

R2=5+9+9+14+14+17+17+17+19,5+19,5=141

Для проверки правильности вычислений можно воспользоваться другим правилом:

R1+R2 = 0,5×(n1+n2)×(n1+n2+1)

В нашем случае R1+R2=69+141=0,5×20×21=210.

Статистика U1=69–10×11 / 2 = 14, U2=141–10×11/2 = 86. Для проверки одностороннего критерия выбираем минимальную статистику U1=14 и сравниваем ее с табличным значением (таблица 4) для n1=n2=10 и уровня значимости 1 %, равного 19. Так как вычисленное значение критерия меньше табличного, нулевая гипотеза отвергается на выбранном уровне значимости, и различия между выборками признаются статистически значимыми с вероятностью более 99%. Таким образом, вывод о существовании различий, сделанный с помощью параметрического критерия Стьюдента, подтверждается с помощью данного непараметрического метода.

В случае попарно связанных выборок применяется T-критерий Уилкоксона. При этом ранжируют попарные разности — положительные и отрицательные (кроме нулевых) — в один ряд так, чтобы наименьшая абсолютная разница (без учета знака) получила первый ранг, одинаковым величинам присваивают один ранг. Отдельно вычисляют сумму рангов положительных (T+) и отрицательных разностей (T–), меньшую из двух таких сумм без учета знака считают тестовой статистикой данного критерия. Нулевую гипотезу принимают на данном уровне значимости, если вычисленная статистика превзойдет табличное значение (таблица 5) (число парных наблюдений уменьшают на число исключенных нулевых разностей). Таким образом, можно сказать, что если нулевая гипотеза верна, статистики T+ и T– примерно равны, сравнительно малые или большие значения Т статистик заставят нас отклонить нулевую гипотезу об отсутствии различий.

902

Пример 7.

Допустим, в результате проведения эксперимента был вычислен ряд попарных разностей между показателем эффекта в двух попарно связанных группах (n1=n2=10) (например, так называемая задача «до и после»):

0,2 -0,4 0,7 -0,9 1,3 1,5 -0,1 0,8 -1,0 1,1.

Ранжируем попарные разности в один ряд независимо от знака разности, получаем следующий ранжированный ряд:

Рассчитаем отдельно сумму рангов положительных (T+) и отрицательных (T–) разностей, в нашем случае

T+ = 2+4+5+8+9+10 = 38, T– = 1+3+6+7=17. Для проверки двустороннего T-критерия используем меньшую статистику T–=17, сравним ее с табличным значением (таблица 4) для числа попарных разностей n=10 и уровня значимости 5 %. Такое табличное критическое значение равно 9. Рассчитанное минимальное значение Т статистики превосходит соответствующее табличное значение, а значит нулевая гипотеза остается в силе.

В случае анализа результатов доклинических исследований непараметрические критерии бывают также полезны при качественной или альтернативной форме представления признаков. Этот вопрос будет рассмотрен нами подробнее в соответствующем разделе.

7.Сравнение нескольких параллельных групп

иповторных (многократных) измерений

Приведенный выше критерий Стьюдента может быть использован для проверки гипотезы о различии средних только для двух независимых групп. Если схема эксперимента предполагает сравнение большего числа групп по значениям количественного признака, совершенно недопустимо сравнивать их попарно на уровне значимости 5 %, поскольку это приведет к росту вероятности ошибки I рода (проблема множественных сравнений). Для корректного решения этой задачи в случае количественных переменных применяется дисперсионный анализ ANOVA [4, 7, 9, 13, 18, 19]. Однако дисперсионный анализ позволяет проверить лишь нулевую гипотезу о равенстве всех средних (соответствующая альтернативная гипотеза — хотя бы одно среднее значение отличается от остальных). Дисперсионный анализ является параметрическим методом, кроме того, необходимо учитывать степень различий выборочных дисперсий сравниваемых выборок. Хотя дисперсионный анализ является параметрическим методом, он достаточно устойчив к отклонениям распределения показателя от нормального закона, однако получаемые с его помощью результаты могут оказаться некорректными в присутствии относительно большого числа резко отличающихся наблюдений. Если в ходе дисперсионного анализа нулевая гипотеза отвергается, этот метод не позволяет узнать, какое именно групповое среднее значение отличалось от других. Для этого на втором этапе анализа используются методы множественного сравнения, которые позволяют поддерживать заданное значение суммарного уровня значимости для всех выполняемых сравнений.

Среди них наиболее известны критерий Стьюдента для множественных сравнений, критерий Ньюмена-Кейлса, критерий Тьюкки, критерий Даннета.

Рассмотрим лишь некоторые из них. Еще раз обращаем внимание, что к применению этих критериев надо прибегать лишь в случае, если дисперсионный анализ показал наличие значимых различий между какими-то средними значениями выборок.

Буквой m обозначим число сравниваемых групп.

Критерий Стьюдента для множественных сравнений основан на использовании неравенства Бонферрони [4, 25]: если k раз применить критерий с уровнем значимости a, то вероятность хотя бы в одном случае найти различие там, где его нет, не превышает произведения k на a. Из неравенства Бонферрони следует, что если мы хотим обеспечить вероятность

903

ошибки a¢, то в каждом из сравнений мы должны принять уровень значимости a¢/k — это и есть поправка Бонферрони (k — число сравнений). Число степеней свободы для критерия Стьюдента при множественном сравнении равно f = m × (n–1), где n — объем группы.

Этот метод хорошо работает, если число сравнений невелико, обычно не больше 8. При большом числе сравнений критерий Ньюмена-Кейлса и критерий Тьюкки дают более точную оценку вероятности a¢ [4,7,15].

Иногда задача заключается в том, чтобы сравнить несколько групп с единственной — контрольной. Конечно, можно использовать любой из указанных выше методов: попарно сравнить все группы, а потом выбрать только те сравнения, в которых участвовала контрольная группа. Однако из-за большого числа лишних сравнений критическое значение окажется неоправданно высоким. Для решения этой задачи статистики существуют специальные методы, например, еще одна модификация критерия Стьюдента с поправкой Бонферрони и критерий Даннета.

В случае поправки Бонферрони необходимо учесть реальное число сравнений для этой задачи (оно равно числу групп m минус один) и, соответственно рассчитать уровень значимости a=a¢/(m – 1) [4].

Критерий Даннета более чувствительный, чем предыдущий, особенно при большом числе групп. Критерий Даннета вычисляется как [4]:

где — оценка внутригрупповой дисперсии, и — сравниваемые средние значения, nk и nc — численность групп.

Сначала средние значения для всех групп упорядочиваются по абсолютной величине их отличия от контрольной группы, сравнения начинают с группы, наиболее отличающейся от контроля. Вычисленное значение q’ сравнивается с табличным (таблица 9) значением, и, если оно превосходит табличное, статистически значимое различие существует. Число степеней свободы для этого критерия равно f = N–m, где N — суммарная численность всех групп, m — число групп. Если различия с очередной группой не найдены, сравнения прекращаются.

Непараметрический критерий Краскела–Уоллиса для сравнения нескольких выборок является напараметрическим аналогом параметрического дисперсионного анализа ANOVA. Он основан на построении объединенного вариационного ряда из вариант рассматриваемых выборок и присвоении рангов всем вариантам в объединенном ряду объемом N. Далее вычисляются статистики Ri для каждой рассматриваемой выборки отдельно, равные суммам рангов в обобщенном ряду вариант, входящих в данную i-ую выборку. При этом для каждого наблюдения в конкретной выборке мы можем указать средний ранг, равный Ri/ni, для всех i от 1 до m. Если выполняется нулевая гипотеза и все совокупности имеют одно и тоже распределение, то можно ожидать, что все средние ранги примерно равны. А именно они примерно равны общему среднему рангу R:

(19)

В качестве статистики критерия используется мера, которая чувствительна к отклонению выборочного Ri/ni от теоретического значения R:

Сумма берется по всем m выборкам.

904

Проверить статистику Краскела–Уоллиса можно по специальным таблицам [9, 12, 15]. Однако, если почти все ni>5, то удобна аппроксимация, которая основана на том, что

вии справедливости нулевой гипотезы. Таким образом, рассчитав значение статистики K, его сравнивают с критическим значением распределения Хи-квадрат (таблица 2),

умноженным на коэффициент . Если вычисленное значение К превосходит

скорректированное критическое, нулевая гипотеза отвергается на уровне значимости a % и различия считаются статистически значимыми.

Для анализа повторных измерений может применяться специальный вариант дисперсионного анализа ANOVA с повторными измерениями (параметрический подход), при этом тестируется нулевая гипотеза о равенстве всех средних значений показателя во всех точках повторных измерений (альтернативная гипотеза — хотя бы одно такое среднее значение в какой-то временной точке отличается от остальных). В качестве непараметрического аналога такого дисперсионного анализа может применяться критерий Фридмана [4, 18, 19]. Если нулевую гипотезу удается отвергнуть, то на втором этапе анализа сравнение между парами временных точек проводится с помощью подходящих параметрических или непараметрических парных статистических тестов. Хотя не во всех исследованиях результаты такого подхода могут быть корректно интерпретированы. Если позволяет дизайн и цель исследования, могут применяться подходящие обобщенные меры, характеризующие динамику показателя: наклон индивидуальной регрессионной зависимости, время до достижения пика, площадь под кривой и т.п.

Пример 8.

Применение критериев множественного сравнения проиллюстрируем на примере результатов эксперимента из примера 1, относящихся к содержанию креатинфосфата в ткани сердца животных групп 1, 2 и 3 (столбцы 1–3 таблицы 11). Группу 1 будем считать контрольной и сравним полученные в этой группе результаты с результатами в группах 2 и 3 с помощью критерия Даннета. Прежде всего, вычислим для этих групп средние значения и дисперсии: Рассчитаем величины отклонений средних значений групп 2 и 3 от среднего значения контрольной группы 1, эти отклонения равны соответственно 4,7 и 2,1. Таким образом, сначала будем определять значения критерия Даннета для сравнения контрольной группы с группой 2, а затем, если статистически значимое различие будет установлено, с группой 3. Поскольку предполагается, что дисперсии сравниваемых групп одинаковы (критерий Фишера), вели-

для сравнения контрольной группы с группой 2 и 3 соответственно равны:

Число степеней свободы в данном случае равно 30–3=27, уровень значимости выберем равным 5 %, тогда по таблице 9 критическое значение равно 2,33. Вычисленные значения критерия превзошли критическое табличное, значит, различия между контрольной и двумя другими группами можно признать статистически значимыми на выбранном уровне значимости.

Критерий Стьюдента с поправкой Бонферрони. По-прежнему сравниваем 2-ю и 3-ю группы с контрольной 1-й. Для этих двух сравнений рассчитываем по формулам 7 и 9

905

значения критерия Стьюдента (аналогично примеру 4). Получаем значения t=6,35 для сравнения со второй группой и t=2,65 для сравнения с третьей. Однако в данном случае уровень значимости выбираем из расчета 0,05/2 = 0,025, число степеней свободы равно f=3×(10–1)=27. Соответствующее значение в таблице распределения Стьюдента приблизительно равно 2,5 (для сравнения — без учета поправок оно было бы равно 2,05). Рассчитанные нами значения t-критерия превзошли выбранное критическое значение, а значит, нулевая гипотеза отвергается и различия признаются статистически значимыми на уровне значимости (для всего критерия) 5 %. В данном случае мы не делаем заключения о различии групп 2 и 3 между собой.

Для сравнения этих трех групп применим непараметрический подход, для этого проанализируем эти же данные с помощью критерия Краскела–Уоллиса. Как и для критерия Уилкоксона–Манна–Уитни мы будем использовать ранги вариант в объединенной совокупности. Как и раньше одинаковым вариантам присваиваем средний ранг так, чтобы последнее значение ранга было равно объему объединенного ряда.

Группа 1: 12 13 14 15 14 13 13 10 11 16

Ранги 19,5 24 27,5 29 27,5 24 24 12,5 15,5 30 R1= 233,5 Группа 2 8 8 9 10 7 7 9 9 11 6

Ранги 5 5 9 12,5 2,5 2,5 9 9 15,5 1 R2= 71 Группа 3 8 9 9 11 12 12 13 13 12 11

Ранги 5 9 9 15,5 19,5 19,5 24 24 19,5 15,5 R3= 160,5.

Как и раньше сумма всех рангов должна быть равна 0,5×N×(N+1), где N — объем обобщенного ряда. В нашем случае сумма рангов должна быть равна 465. Рассчитываем статистику Краскела-Уоллиса:

Тестовая статистика ; критическое значение критерия χ2 для 2 степе-

ней свободы и уровня значимости 5 % (таблица 2) равно 5,99. Поскольку вычисленное значение критерия превзошло соответствующее табличное на уровне значимости 5 %, нулевая гипотеза отвергается и различия между всеми тремя группами признаются статистически значимыми.

8. Альтернативная форма учета реакций

Всестороннее изучение картины действия исследуемого лекарственного препарата требует выделения сопоставимых параметров. Эта задача решается, например, если из всей массы наблюдений использовать для статистического анализа только наблюдения за исходами в дихотомической форме, например, погибло животное или выжило. Так при изучении наркотических средств можно учитывать реакцию по тому, перешло или не перешло животное в «боковое положение»; при изучении противосудорожных средств — предотвращена или нет судорожная реакция и т.д. Все эти примеры иллюстрируют способ учета реакции в альтернативной форме, то есть реакции, которая или наступает, или нет. Альтернативное распределение — это распределение элементов совокупности на две части (две альтернативы) по какому-либо признаку, чаще всего по качественному. Эти признаки не связаны между собой никакими арифметическими соотношениями, упорядочить их невозможно. Единственный способ описания качественных признаков состоит в том, чтобы подсчитать число объектов, имеющих одно и то же значение или долю от общего числа объектов, которая приходится на то или иное значение. Надо сказать, что качественные переменные могут иметь число градаций больше двух, тогда для их анализа применяются статистические методы сравнения распределений.

В случае качественной классификации невозможно ввести такие количественные параметры, как математическое ожидание, дисперсия и др. Тем не менее можно указать

906

определенный численный параметр, имеющий вполне точный и объективный смысл: доля вариант одного типа. Так для альтернативного распределения доля

(21)

где n1, n2 — численности альтернатив; N=n1+n2 — численность всей совокупности. Кроме того, доля может быть выражена в процентах:

(22)

В отношении доли вариант в альтернативном распределении возникают те же статистические задачи, что и для параметров, представленных в количественной форме:

—оценка доли p в генеральной совокупности по выборочным данным, нахождение доверительного интервала для p;

—выявление различия между генеральными долями p1 и p2 двух совокупностей по выборочным данным, т.е. cравнение двух выборочных долей вариант.

Формулы (21–22) позволяют рассчитать выборочную оценку генеральной доли p. Поскольку в эксперименте участвует ограниченное количество животных, возникает вопрос об определении доверительного интервала для p. Строго эта задача решается с использованием биномиального распределения [4, 7, 12, 19, 21]. Соответствующие расчеты очень громоздки, поэтому составлены таблицы [12] и номограммы [19], в которых можно сразу найти 95 % и 99 %-ные доверительные границы для выборочной доли. Ввиду большого объема этих таблиц они обычно приводятся лишь в специальных справочниках. Поэтому на практике часто пользуются различными приближенными методами. Как правило, применяется нормальное приближение, то есть аппроксимация биномиального распределения нормальным. Из центральной предельной теоремы следует, что при достаточно большом объеме выборки выборочная оценка доли приближенно подчиняется

нормальному закону распределения, имеющему генеральное среднее и стандартное отклонение, равное стандартной ошибке доли σp.

При таком подходе доверительные границы для генеральной доли определяются как p ± zα × σp, где σp — стандартная ошибка доли, задается соотношением:

(23)

а zα — определяется по значению доверительной вероятности по таблице 7 (обычно в случае доклинических исследований P=95 % и соответствующее значение Z=1,96).

При малых объемах выборок нормальное приближение дает слишком неточные результаты. Условием применимости аппроксимации с помощью нормального распределения в данном случае является выполнение соотношения n×p<5. В случае невыполнения этого условия для исправления положения Р. Фишер предложил пользоваться угловой трансформацией, или, проще говоря, вспомогательной величиной j, связанной с p равенством:

(24)

Эта величина имеет распределение, близкое к нормальному. Порядок действий предполагается следующий: для получения доверительных границ для доли вариант сначала

нужно найти значение j и вычислить интервал Затем по формуле

пересчитать полученные для j значения границ, вернувшись снова к значениям p. Конечно, переход от p к j и обратно с применением таблицы тригонометрических функций до-

907

статочно неудобен. Поэтому была составлена специальная таблица, которая непосредственно связывает значения p и j (таблица 6).

Еще одна задача возникает при анализе выборочных долей и требует внимания. При значениях p, близких к 0 или 1 (то есть при нулевом или 100 % эффекте) в случае малого объема выборки условия центральной предельной теоремы нарушаются, и при этом нужно несколько изменить процедуру построения доверительных интервалов.

8.1. Статистические оценки нулевого и 100 % эффекта

Очевидно, что любой признак, наблюдавшийся в 100 % случаев, у группы, состоящий из 10 вариант, может в большой мере объясняться случайным совпадением и не воспроизводиться в дальнейшем при продолжении исследований. Тот же признак, наблюдаемый в 100 % случаев у группы, состоящей из 1000 вариант, имеет гораздо большую достоверность. Поэтому даже в случае появления в исследовании 0 или 100 % долей, эти результаты должны быть скорректированы.

Для этого можно пользоваться следующим подходом: рассматривать возможный процент противоположного эффекта при дальнейшем увеличении числа подобных наблюдений и его стандартную ошибку:

(25)

(26)

где a — полученный в эксперименте обобщенный показатель (0 %), p — скорректированное значение этого показателя в %.

Доверительный интервал для скорректированного значения доли задается соотношением: a±t×σp, где t определяется по таблице 1 для выбранного уровня значимости и объема выборки.

Пример 9.

Лабораторным животным вводили гепатопротектор, и о его эффективности судили по действию гексенала (40 мг/кг), который вызывает у животных сон. Контрольная группа состояла из 36 животных, а получавшая гепатопротектор — из 25. Если животное перешло в состояние сна — будем обозначать такой исход как «ДА».

Таким образом, доля животных перешедших в состояние сна, например, в получавшей гепатопротектор группе, равна p=9/25=0,36 или 36 %. Ошибка выборочной доли в данном случае равна σp=0,096 или 9,6 %. Соответствующий 95 % доверительный интервал для выборочной доли заключается между 0,17 и 0,55 или, другими словами, между 17 % и 55 %. Рассчитаем доверительный интервал для выборочной доли с учетом угловой трансформации. По таблице 6 находим для доли 0,36 значение j =1,287. Границы 95 % доверительного интервала задаются соотношением

908

и в нашем случае получаем диапазон от 0,9 до 1,68 (значение zα=1,96 определяем по таблице 7 для уровня значимости 5 %). Теперь по таблице 6 по рассчитанным граничным значениям j определяем значения p, соответствующие границам доверительного интервала, получаем диапазон от 0,19 до 0,55. И хотя этот интервал достаточно широк, он имеет практическое значение.

Проиллюстрируем ситуацию с возникновением в получавшей гепатопротектор группе так называемого нулевого эффекта. Допустим, что в таблице 14 в получавшей гепатопротектор группе ни одно животное из 25 не перешло в сон (0%).

Тогда

95 % доверительный интервал для этой выборочной доли заключен между значениями 0 % ÷ 0 + 2,06×3,57 % (так как доля не может иметь отрицательное значение) или можно записать, что доля животных в получавшей гепатопротектор группе, перешедших в сон, равна 0 ± 3,57 (0 ÷ 7,35) %. Таким образом, несмотря на нулевой эффект в исследовании с использованием 25 животных, с вероятностью более 95 % можно утверждать, что при продолжении исследований доля животных, переходящих в сон, будет заключена в пределах от 0 % до 7,35 % случаев. При этом с вероятностью более 95 % можно сказать, что при продолжении исследований доля противоположных исходов будет не менее чем 92,65 % животных.

8.2. Оценка разности между долями

Поскольку выборочная доля аналогична выборочному среднему, задача оценки разности между долями решается аналогично задаче оценки разности между средними значениями. При этом также можно использовать различные параметрические и непараметрические методы сравнения.

Рассмотрим параметрический критерий Стьюдента для сравнения долей в двух параллельных группах. Рассчитываемая тестовая статистика t представляет собой отношение разности выборочных долей к стандартной ошибке разности выборочных долей:

(27)

где p1, p2 — сравниваемые выборочные доли, σdp — стандартная ошибка разности выборочных долей.

Нулевая гипотеза в данном случае состоит в том, что p1=p2. И ее отвергают, если рассчитанная статистика t превзойдет табличное значение, выбранное в соответствии с заданным уровнем значимости a и числом степеней свободы f=n1+n2–2.

Ошибка разности между долями, взятыми из приблизительно равновеликих выборок (объем выборок отличается менее чем на 25%), вычисляется по формуле:

(28)

В случае, когда сравнивают доли из неравновеликих выборок и при 75%≥p≥25%, ошибку разности долей определяют по формуле:

(29)

где p определяют как средневзвешенную из p1 и p2 долей:

(30)

Если доли выражают в процентах от n, то в приведенных формулах вместо 1–p нужно брать 100–p.

909

Описанный выше критерий проверки равенства долей в двух выборках применим при не слишком больших и не слишком малых значениях p (25 %≤p≤75 %). Особенно это важно учитывать в случае малых выборок. Свободным от подобного рода ограничений и более универсальным оказывается способ проверки равенства долей, основанный на j-преобразовании Фишера. Для компенсации ошибок вводится специальная поправка Йейтса, называемая также поправкой на непрерывность, равная 1/(2×n). Эту поправку вычитают из большей и прибавляют к меньшей доле. Затем исправленные доли в % трансформируют с помощью таблицы 6. С учетом этой поправки величина критерия определяется формулой:

(31)

ϕ — угловая трансформация частоты, задаваемая формулой (24).

Повторим, что условием для неприятия нулевой гипотезы служит превышение рассчитанным значением статистики t соответствующего табличного значения (таблица 1 критерия Стьюдента) для выбранного уровня значимости и числа степеней свободы f=n1+n2–2.

8.3. Таблицы сопряженности: критерий Хи-квадрат

При проведении исследований для оценки значимости расхождения частот какоголибо явления в двух параллельных группах животных может быть использован непараметрический статистический метод, который носит название критерия χ2. Этот критерий может быть применен, например, при сравнении в эксперименте двух групп животных — получавших исследуемое вещество и контрольной; двух групп животных, получавших два различных сравниваемых по своей активности вещества; двух групп животных, получавших различные дозы изучаемого препарата или одну и ту же дозу различными путями введения и т.д. Для описания результатов такого эксперимента удобно применять таблицы сопряженности, в которой для каждой из групп указывается число животных с каждым из двух альтернативных значений признака. Таким образом, для двух рассматриваемых групп и для двух возможных исходов получается таблица размерности 2×2.

Допустим, в результате проведения исследования было определено, что % погибших животных в получавшей исследуемое вещество группе ниже (или выше), чем в контрольной, но является ли это различие значимым? Для ответа на этот вопрос вычисляется величина статистики χ2, которая является показателем максимально возможных при данном уровне значимости отклонений частот.

Как обычно для анализа таблицы сопряженности выдвигается нулевая гипотеза: отсутствует влияние изучаемого препарата на исход эксперимента. Исходя из нулевой гипотезы, можно посчитать, какова была бы смертность в каждой из групп, если бы смертельные исходы по частоте равномерно распределились в обеих группах. Результаты эксперимента в двух группах объединяются, и определяется процент «хороших» и «плохих» исходов по суммарным результатам в двух группах. При этом рассчитываются таблицы ожиданий, то есть результаты, которые можно было бы ожидать в обеих группах, при правильности нулевой гипотезы и равномерности распределения частот различных исходов в обеих группах. На основании сопоставления таблиц сопряженности и таблиц ожидания составляется таблица отклонений наблюдавшихся частот pn от ожидаемых po. Для расчета величины χ2 из абсолютной величины каждого отклонения вычитают 0,5 (поправка Йейтса), полученную разность возводят в квадрат и результат делят на соответствующее ожидание. Поправка применяется только для таблиц сопряженности 2×2. Статистика c2 представляет собой сумму полученных величин.

(32)

910