ОЭТ / 4.6 Параллельное RLC
.docПараллельные соединения в цепях переменного тока
При параллельном соединении активного сопротивления и индуктивности напряжение на участках цепи одно и то же, а общий ток равен сумме токов отдельных ветвей (рис.1,а).
Рис.1 а) |
|
|
Построим векторную диаграмму. Сначала строим вектор напряжения U, потом векторы токов (рис.1,б). Ток Ia, протекающий через сопротивление, совпадает с вектором напряжения и называется активным током. Реактивным является ток индуктивности IL и он отстает от напряжения на 90º. Результирующий ток I отстает от напряжения на угол φ.
Так как результирующий ток отстает от напряжения, то при напряжении u = Umsinωt в соответствии с векторной диаграммой ток i=Im(sinωt - φ).
Из треугольника токов следует, что активный, реактивный и полный токи связаны между собой, как стороны прямоугольного треугольника:
![]() ,
Ia
= Icosφ,
IL
= Isinφ.
,
Ia
= Icosφ,
IL
= Isinφ.
Стороны треугольника токов можно разделить на напряжение U и получить треугольник проводимостей (рис1,в), где:
полная проводимость цепи Y = I/U;
активная проводимость G = Ia/U;
реактивная проводимость ВL = IL/U.
Установим соотношения между сопротивлениями и проводимостями:
![]() ;
;
![]() ;
;
![]() Y
= I/U
= 1/Z.
Y
= I/U
= 1/Z.
Кроме того,
сosφ = G/Y; sinφ = ВL /Y; tgφ = ВL /G.
Аналогично рассматривается параллельное соединение активного сопротивления и емкости (рис.2): схема включения (а), треугольники токов (б), проводимостей (в) и мощностей (г).
Рис.2 а) |
б) |
в) |
г) |
При параллельном соединении R, L и C напряжение на элементах цепи одинаковое (рис.3,а). Ток IR будет током активным: Iа = IR =U/R.
Ток IС будет током реактивным, опережающим по фазе напряжение на четверть периода и IС = U/XС. Ток IL будет током реактивным, отстающим по фазе от напряжения на четверть периода и IL = U/XL.
1.
IL
>
IС.
Проводим вектор напряжения и строим
векторную
диаграмму (рис.3,б). Реактивный ток равен
разности индуктивного и емкостного
токов: IР
=
IL
IС.
Общий ток
![]() отстает от напряжения на угол φ, т.е.
общее сопротивление цепи носит
индуктивный характер (ВL>
ВC).
отстает от напряжения на угол φ, т.е.
общее сопротивление цепи носит
индуктивный характер (ВL>
ВC).
Рис.3 а) |
б) в) |
Из закона Ома известно, что ток прямо пропорционален приложенному напряжению и проводимости цепи. Тогда:
I = U/Z = UY, т.е. Y=1/Z; где Y—полная проводимость;
Iа
= Icosφ
=
![]() .
.
![]() ,
где G—активная
проводимость;
,
где G—активная
проводимость;
![]() .
.
![]() ,
где В
— реактивная проводимость.
,
где В
— реактивная проводимость.
Если
токи разделить на напряжение, получим
треугольник проводимостей (рис.3,в).
Полная проводимость
![]() ;
cosφ
= G/Y;
sinφ
= B/Y.
;
cosφ
= G/Y;
sinφ
= B/Y.
Для мощностей можно записать: Р=U2G=UIa; Q=U2B = UIP; S = UI.
2. IL > IС (ВL ВC). Общий ток опережает напряжение на угол φ, т.е. общее сопротивление цепи носит емкостной характер. На рис.4 изображены векторная диаграмма токов и напряжения (а), а так же треугольник проводимостей (б). |
Рис.4: а) б) |
3. IL = IС (ВL= ВC): резонанс токов. В этом случае IР = IL IС = 0 и общая реактивная проводимость равна нулю. Общий ток совпадает по фазе с напряжением и равен активной составляющей тока: I=Ia=U/G; сosφ=1; Р= I2R. |
Рис.5 |
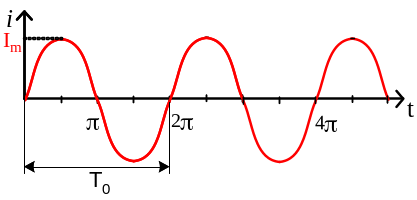
При резонансе
энергии в конденсаторе и катушке равны:
![]() .
.
Подставив в это
уравнение Um
= ω0LIm
и преобразовав
его, получим резонансную
частоту и период:
![]() T0
=2π
T0
=2π![]()
![]() .
.
Так как
![]() ,
то волновое сопротивление контура
,
то волновое сопротивление контура
![]()
При резонансе проводимости реактивных элементов равны
Реактивные токи
IL=IC=UYB
=
Тогда
Количественно данное явление характеризуется добротностью контура Q
Чем меньше потери в цепи (при большем R), тем больше добротность контура. Резонанс токов возникает, когда частота источника энергии f равна резонансной частоте f0 (рис.6). Рис.6. |
|
Метод активных и реактивных токов
1.
Рассчитать реактивные составляющие
ветвей: XL1=ωL1;
2. Рассчитать реактивные сопротивления ветвей X1=Σ XL1i - ΣXС1i; X2=Σ XL2i -Σ XС2i. |
|
3. Рассчитать полные сопротивления ветвей:
Z1
=![]() Z2
=
Z2
=![]()
4. Найти cosφ и sinφ каждой ветви:
cos φ1 = R1/Z1; sin φ1 = X1/Z1; cos φ 2 = R 2/Z 2; sin φ 2 = X 2/Z 2.
5.
Найти токи в ветвях:
![]()
![]()
6. Рассчитать активные и реактивные составляющие токов ветвей:
I1a=I1 cos φ1; I1Р=I1 sin φ1; I2a=I2 cos φ2; I2Р=I2 sin φ2.
7. Рассчитать общие активный и реактивный токи: Ia=I1а + I2а; Iр=I1р I2р.
8.
Рассчитать
S
= UIа;
Q = U IР;
Р
= U
I;
![]() Z=U/I.
Z=U/I.
Энергетические процессы при резонансе токов
Колебательный
процесс в контуре заключается во
взаимном преобразовании энергии
электрического и магнитного полей.
Предположим, что конденсатор зарядился
и имеет запас энергии
![]() .
В t=0
он переключается
на индуктивность (рис.8,а).
.
В t=0
он переключается
на индуктивность (рис.8,а).
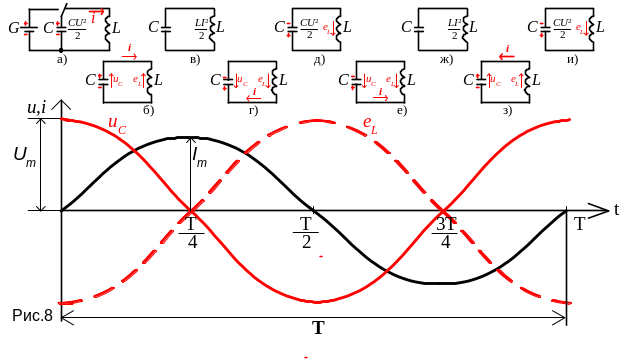
В первую четверть периода (0 - T/4) конденсатор играет роль источника энергии и разряжается через индуктивность, в цепи существует ток (рис.8,б). Увеличение тока вызывает возникновение ЭДС самоиндукции eL. Энергия электрического поля конденсатора переходит в магнитное поле катушки. ЭДС самоиндукции уравновешивает напряжение на конденсаторе: uC = eL.
В t=Т/4
энергия электрического поля конденсатора
полностью перешла в энергию магнитного
поля катушки
![]() :
i
= Im;
uC
= eL
= 0 (рис.8,в).
:
i
= Im;
uC
= eL
= 0 (рис.8,в).
Во вторую четверть периода (Т/4 - T/2) ток уменьшается, сохраняя направление. ЭДС меняет свой знак, стремясь поддерживать ток. Индуктивность играет роль источника энергии и конденсатор заряжается с изменением полярности (рис.8,г). Энергия магнитного поля переходит в электрическое поле конденсатора. В t=Т/2 энергия магнитного поля катушки полностью перешла в энергию электрического поля конденсатора: i = 0, uC = Um (рис.8,д).
В третью четверть периода (Т/2 - 3/4Т) конденсатор разряжается через индуктивность и играет роль источника энергии. Энергия переходит в магнитное поле катушки (рис.2,е). В t=3/4Т энергия электрического поля конденсатора полностью перешла в энергию магнитного поля катушки (рис.8,ж).
В последнюю четверть периода (3/4Т - T) ток уменьшается, сохраняя направление. Индуктивность играет роль источника энергии и заряжает конденсатор с изменением полярности (рис.8,з). В t=Т энергия магнитного поля катушки полностью перешла в энергию электрического поля конденсатора (рис.8,и). После этого процесс повторится.
Рис.9 а) |
б) |
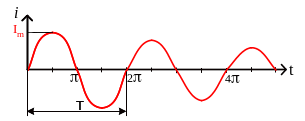
Таким образом, в контуре, состоящем из параллельно включенных индуктивности и конденсатора, создаются незатухающие колебания с периодом Т0 (рис.9,а). В реальном колебательном контуре запас энергии сокращается за счет потерь. Поэтому амплитуда тока с каждым периодом уменьшается и процесс называется апериодическим (рис.9,б).
|
|
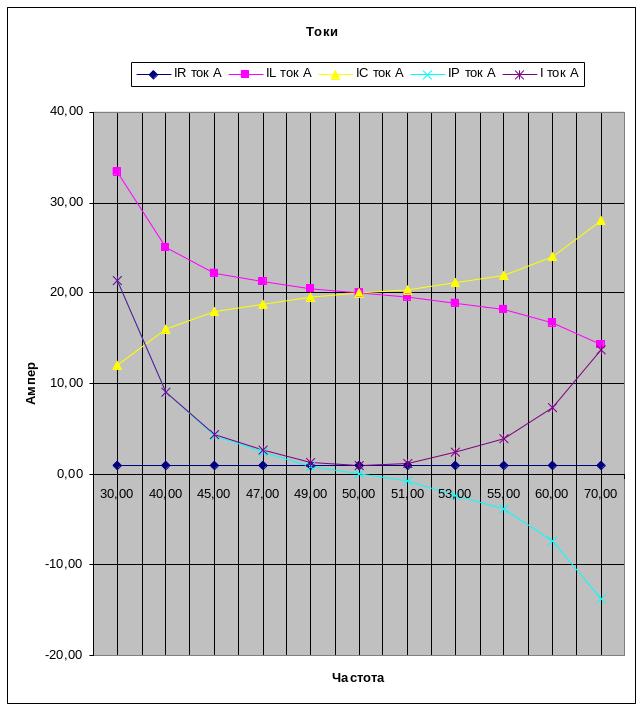
Расчет параллельного колебательного контура:
L |
мГн |
15,9 |
15,9 |
15,9 |
15,9 |
15,9 |
15,9 |
15,9 |
15,9 |
15,9 |
f |
Гц |
40,00 |
45,00 |
47,00 |
49,00 |
50,00 |
51,00 |
53,00 |
55,00 |
60,00 |
Т |
сек |
0,0250 |
0,0222 |
0,0213 |
0,0204 |
0,0200 |
0,0196 |
0,0189 |
0,0182 |
0,0167 |
ω |
|
251,20 |
282,60 |
295,16 |
307,72 |
314,00 |
320,28 |
332,84 |
345,40 |
376,80 |
XL |
Ом |
3,99 |
4,49 |
4,69 |
4,89 |
4,99 |
5,09 |
5,29 |
5,49 |
5,99 |
C |
мкФ |
637 |
637 |
637 |
637 |
637 |
637 |
637 |
637 |
637 |
Хc |
Ом |
6,25 |
5,56 |
5,32 |
5,10 |
5,00 |
4,90 |
4,72 |
4,55 |
4,17 |
R |
Ом |
100 |
100 |
100 |
100 |
100 |
100 |
100 |
100 |
100 |
Z |
Ом |
11,00 |
22,89 |
37,06 |
76,70 |
99,96 |
79,43 |
39,79 |
25,49 |
13,55 |
U |
В |
100 |
100 |
100 |
100 |
100 |
100 |
100 |
100 |
100 |
S |
Bт |
909,08 |
436,95 |
269,86 |
130,38 |
100,04 |
125,90 |
251,35 |
392,3 |
737,9 |
Q |
BАр |
903,56 |
425,35 |
250,64 |
83,66 |
2,78 |
-76,49 |
-230,60 |
-379,3 |
-731,1 |
P |
Bт |
100,00 |
100,00 |
100,00 |
100,00 |
100,00 |
100,00 |
100,00 |
100,0 |
100,0 |
cos φ |
|
0,11 |
0,23 |
0,37 |
0,77 |
1,00 |
0,79 |
0,40 |
0,25 |
0,14 |
IR |
А |
1,00 |
1,00 |
1,00 |
1,00 |
1,00 |
1,00 |
1,00 |
1,00 |
1,00 |
IL |
А |
25,04 |
22,26 |
21,31 |
20,44 |
20,03 |
19,64 |
18,90 |
18,21 |
16,69 |
IC |
А |
16,00 |
18,00 |
18,80 |
19,60 |
20,00 |
20,40 |
21,20 |
22,00 |
24,00 |
IР |
А |
9,04 |
4,25 |
2,51 |
0,84 |
0,03 |
-0,76 |
-2,31 |
-3,79 |
-7,31 |
I |
А |
9,09 |
4,37 |
2,70 |
1,30 |
1,00 |
1,26 |
2,51 |
3,92 |
7,38 |

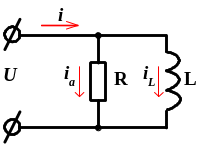
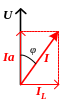 б)
б)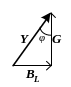 в)
в)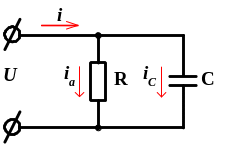
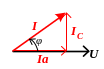

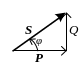

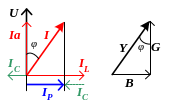
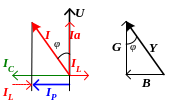
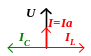
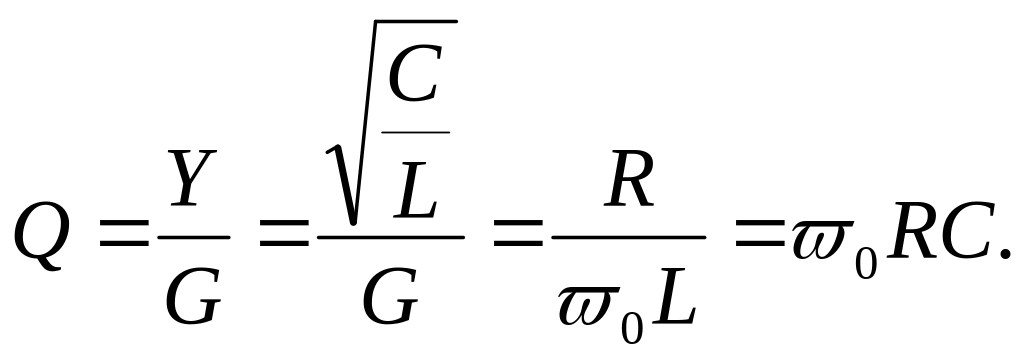
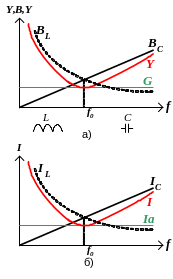
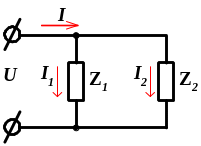 Рис.7
Рис.7