Инж.гр. Лекции, теория / Методы проецирования. Проецирование центральное

Тема3. Проекционное черчение

3.1.Методы проецирования. Проецирование центральное и параллельное. Ортогональные проекции

Проецированием называется процесс построения изображения предмета путем проведения через все точки предмета проецирующих лучей до пересечения с плоскостью проекций.

Проекцией называется изображение предмета, полученное в результате проецирования его на какую-либо плоскость проекций.

Проецирование осуществляют двумя методами:

1.Центральное проецирование или перспектива, при котором проецирующие лучи пересекаются в одной точке (рис.1,а и рис.2,а). Этот метод применяется в живописи и архитектуре.

2.Параллельное проецирование, при котором проецирующие лучи между собой параллельны. Полученная проекция называется параллельной.

Рисунок 1. Методы проецирования

Параллельное проецирование бывает:

а) косоугольное проецирование, при котором параллельные проецирующие лучи направлены под острым углом к плоскости проекций

(рис.1, б и рис.2, б).

б) прямоугольное или ортогональное проецирование (рис.1, в и рис.2, в), при котором проецирующие лучи перпендикулярны плоскости проекций. Этот метод в черчении применяют наиболее часто.

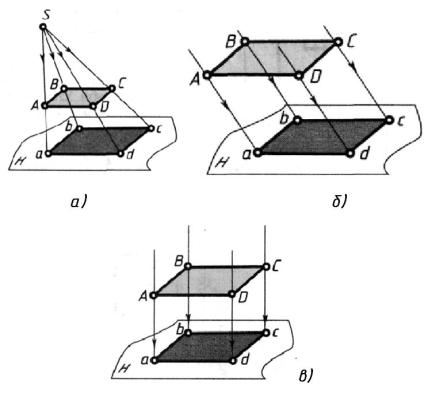
Рисунок 1. Методы проецирования на примере четырехугольника

Полученная проекция при прямоугольном проецировании называется

прямоугольной или ортогональной.

При ортогональном проецировании предмет располагают перед плоскостью проекций так, чтобы большинство его линий и плоских поверхностей были параллельны этой плоскости (рис.3). Тогда эти линии и поверхности будут изображаться на плоскости проекций в действительном виде, без искажений.

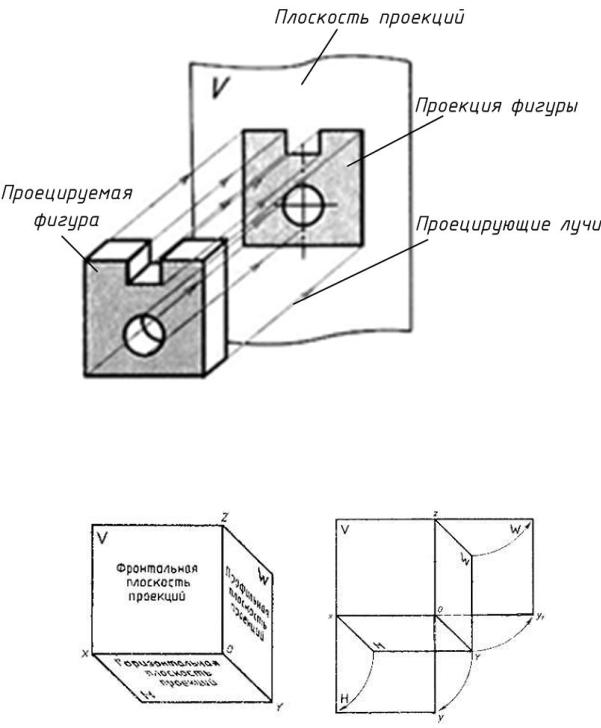
Рисунок 3. Прямоугольное (ортогональное) проецирование

Ортогональное проецирование - проецирование на три взаимно перпендикулярные плоскости проекции – горизонтальную (Н), фронтальную (V) и профильную (W), с помощью лучей, перпендикулярных плоскостям проекции (рис.4).

Рисунок 4. Плоскости проекций при ортогональном проецировании

3.2.Проекции точки

Точка - основной геометрический элемент линии и поверхности, поэтому изучение прямоугольного проецирования предмета начинается c построения прямоугольных проекций точек.

Проецирование точки на плоскость проекций. Дана точка А в

пространстве и плоскость проекций (например, горизонтально расположенная, которую называют горизонтальной плоскостью проекций и

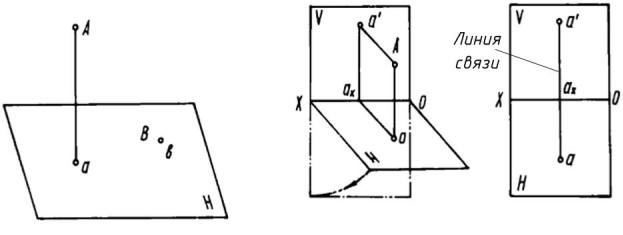
обозначают буквой Н). Спроецируем заданную точку на плоскость с помощью проецирующего луча (рис.5, а). Точку пересечения проецирующего луча с плоскостью проекций обозначают строчной буквой а и называют

горизонтальной проекцией точки А. Проецирующий луч Аа называют

проецирующей прямой. На рисунке 5, а показана горизонтальная проекция точки А, заданной в пространстве, и точки В, лежащей на самой плоскости. Точка В и ее проекция в данном случае совпадают.

Рисунок 5. Проецирование точки

Проецирование точки на две плоскости проекций. По одной проекции точки нельзя судить о ее положении в пространстве. Поэтому добавляется еще одна плоскость проекций V, которая называется фронтальной плоскостью проекций (слово « фронтальная» означает лобовая). Фронтальная и горизонтальная плоскости проекций взаимно перпендикулярны (рис.5,б). Линию пересечения ОХ этих плоскостей называют осью проекций. Точку пересечения проецирующего луча с фронтальной плоскостью проекций называют фронтальной проекцией точки и обозначают а' (читается а штрих).

Полученные две проекции точки будут лежать на двух плоскостях. Чтобы получить их в одной плоскости (на поле чертежа), необходимо мысленно повернуть плоскость Н вокруг оси ОХ на 900 (рис.5,б).

Фронтальная и горизонтальная проекции точки соединены одной прямой – линией связи, перпендикулярной к оси ОХ. Отрезок прямой аах показывает расстояние от точки А до плоскости V, а отрезок а'aх – до плоскости Н.

На рисунке 5, б плоскость V изображена в виде прямоугольника, а плоскость Н — в виде параллелограмма. Наклонную сторону этого параллелограмма обычно проводят под углом 45° к его горизонтальной стороне.

Длина наклонной стороны берется равной 0,5 ее действительной длины.

Из точки А опускают перпендикуляры на плоскости V и Н. Тогда а' и а пересечения перпендикуляров с плоскостями проекций V и Н являются прямоугольными проекциями точки А. Фигура Aaaха' в пространстве — прямоугольник.

Совместим плоскости Н с плоскостью V, вращая V вокруг линии пересечения плоскостей х. В результате получается комплексный чертеж точки А (рис.5, б).

Для упрощения комплексного чертежа границы плоскостей проекций V и Н не указывают (рис.5, в).

Перпендикуляры, проведенные из точки А к плоскостям проекций, называются проецирующими линиями, а' — фронтальная проекция точки А,

а — горизонтальная проекция точки А.

Линия а'а называется вертикальной линией проекционной связи.

Расположение проекции точки на комплексном чертеже зависит от положения этой точки в пространстве.

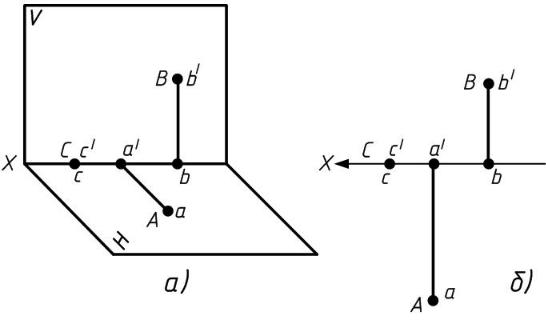
Рисунок 6. Положение точки относительно двух плоскостей проекций

Если точка А лежит на горизонтальной плоскости проекций Н (рис. 6, а), то ее горизонтальная проекция а совпадает с заданной точкой, а фронтальная проекция а' располагается на оси х. При расположении точки В на фронтальной плоскости проекций V ее фронтальная проекция совпадает с этой точкой, а горизонтальная проекция лежит на оси х. Горизонтальная и фронтальная проекции заданной точки С, лежащей на оси х, совпадают с этой точкой. Комплексный чертеж точек А, В и С показан на рис.6,б.

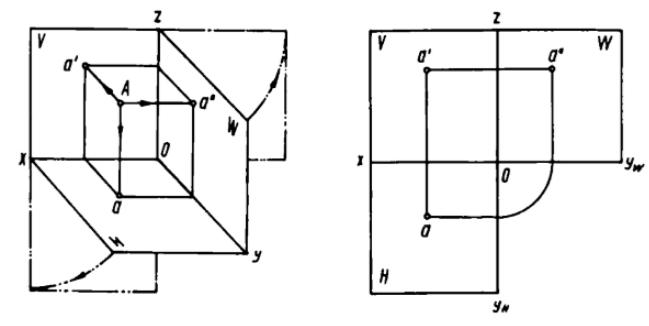
Проецирование точки на три плоскости проекций. На практике нередко возникает необходимость трех проекций изображаемого предмета. Поэтому рассмотрим проецирование точки на три взаимно перпендикулярные плоскости (рис.7, а). Третью плоскость называют профильной и обозначают W.Слово «профиль» означает вид предмета сбоку. Профильную проекцию точки А обозначим а'' (читается а два штриха).

Чтобы все три проекции находились в одной плоскости, повернем плоскости Н и W на 900 до совмещения их с плоскостью V (рис.7, б).

Рисунок 7. Проецирование точки на три плоскости проекций

Проекции точки а и а' будут лежать на одной вертикальной прямой (линии связи), а проекции а' и а'' - на одной горизонтальной прямой (рис.7 )

Наглядное изображение системы из трех плоскостей проекций дано на рисунке 8, а.

Ребра трехгранного угла (пересечение плоскостей проекций) называются осями проекций и обозначаются x, y и z . Пересечение осей проекций называется началом осей проекций и обозначается буквой О. Для получения комплексного чертежа точки А плоскости Н и W совмещают с плоскостью V, вращая их вокруг осей Ox и Oz.Комплексный чертеж точки А показан на рисунке 8,б и в. Проекции точки а и а' будут лежать на одной вертикальной прямой (линии связи), а проекции а' и а'' - на одной горизонтальной прямой.

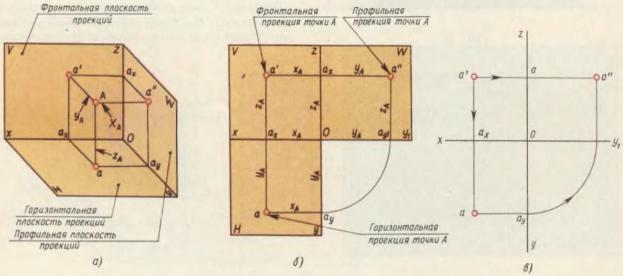
Рисунок 82. Наглядное изображение системы из трех плоскостей проекций и эпюр точки

Отрезки проецирующих линий от точки А до плоскостей проекций называются координатами точки А и обозначаются XA, YA, ZA.Координата ZA точки А (рис.9) равна отрезку а' ах и определяет расстояние от точки А до горизонтальной плоскости проекций Н. Координата YA точки А равна отрезку а ах и определяет расстояние от точки А до фронтальной плоскости проекций V. Координата XA точки А равна отрезку а аy и определяет расстояние от точки А до профильной плоскости проекций W.

Если заданы координаты точки А (например, XA=20 мм, YA =22мм,

ZA =25мм), то можно построить три проекции этой точки. Для этого от начала координат О по направлению оси Oz откладывают вверх координату ZA и вниз координату YA.Из концов отложенных отрезков аz и аy (рис.9,а) проводят прямые-параллельные оси Ох, и на них откладывают отрезки, равные координате XA.Полученные точки а' и а - фронтальная и горизонтальная проекции точки А.

По двум проекциям а' и а точки А построить ее профильную проекцию можно тремя способами:

1)из начала координат О проводят вспомогательную дугу радиусом Оау , равным координате YA (рис.9, б и в), из полученной ау1 проводят прямую, параллельную оси Oz , и откладывают отрезок, равный ZA ;

2)из аy проводят вспомогательную прямую под углом 450 к оси OY (рис.9, а),

получают ау1 ; 3) из начала координат О проводят вспомогательную прямую под углом 450 к

оси OY (рис.9, б), получают ау .