
6 курс / Клинические и лабораторные анализы / Клиническая_оценка_результатов_лабораторных_исследований
.pdf
Рис. 10.5. Кривые вязкости (а) и течения (б) ньютоновской (1), псевдопластичной (2) и дилансной жидкостей (3).
тицы «затруднено» более, чем в случае больших скоростей сдвига, и, во-вторых, взаимодействие между частицами более выражено ввиду их больших относительных размеров при низких скоростях деформации. По-видимому, имеют место оба механизма возникновения псевдопластичности.
Реже, чем псевдопластичные, встречаются дилансные среды. Индекс течения п у них больше единицы. Это означает, что вязкость у таких материалов увеличивается с ростом скорости деформации. Кривые течения и вязкости такой среды представлены на рис. 10.5, а, график 3. Явление дилансии впервые обнаружено О. Рейнольдсом. Необходимо различать реологическую и объемную дилансию. Явление реологической дилансии состоит в увеличе - нии вязкости с ростом скорости деформации вследствие увеличения объема дисперсной фазы системы при деформирующем воздействии. Как более общий случай реологической дилансии можно выделить объемную дилансию, при которой увеличение объема дисперсной фазы не сопровождается изменением кажущейся вязкости среды. Общепринятое толкование дилансии заключается в том, что при сдвиге как бы изменяется «упаковка» частиц твердой дисперсной фазы, она становится более «свободной». Это в свою очередь приводит к увели - чению относительного объема дисперсной фазы. Возникновение такой своеобразной «по - ристой» структуры, в которой жидкие элементы дисперсионной среды сочетаются со своего рода элементами «пустоты», и приводит к феномену дилансии.
До сих пор речь шла о текучих средах с так называемой стационарной реологией. К жидкостям с нестационарной реологией относятся такие, которые обладают свойствами тиксотропии и реопексии. Сущность тиксотропии заключается в том, что при течении с постоянной скоростью деформации неньютоновская жидкость со временем становится нью - тоновской (подчеркнем, что псевдопластичные и дилансные среды также ведут себя как ньютоновские, но лишь в определенных пределах скоростей деформации). В отличие от псевдопластичных сред, структура которых начинает меняться с ростом скорости деформа - ции постепенно, у тиксотропных сред для этого требуется время.
Явлением, противоположным тиксотропии, является реопексия, ил и антитиксотропия. Среды, обладающие свойством реопексии, характеризуются тем, что их вязкость увеличивается в результате возникновения течения. В отличие от дилансных сред для изменения структуры реопектической жидкости необходимо, чтобы прошло определенное время после начала воздействия деформаций.
Таким образом, нами кратко рассмотрены все типы неньютоновских жидкостей в соот - ветствии с приведенной выше классификацией, за исключением нелинейно-вязкопластичных жидкостей. Само название этого типа жидкостей говорит о том, что их главной особенностью является сочетание пластичности и вязкости с уклонением кривых течения от линейной
491





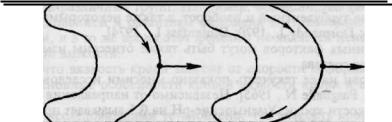
Рис. 10.8. Феномен «переливания цистерны».
Горизонтальными стрелками обозначено направление движения эритроцитов, остальными — направление перемещения оболочки и содержимого эритроцитов.
мостей типа экспоненциальной. Авторов, предлагающих такого типа зависимости, подкупало, по-видимому, то, что этим можно было объяснить «скачки» вязкости, вызываемые зачас - тую незначительным увеличением гематокритного числа.
V. Wand (цит. по E.W. Merril, 1969) предложена следующая формула зависимости вязкости крови от гематокритного числа:
Пкроаи = л™ (1 + 0,25Н + 7,35 • Ю-4 ■ Н2).
По мнению E.W. Merril (1969), эта формула справедлива для гематокритного числа 0—0,5 и области низкой асимптотической вязкости. Любопытно, что пред метом докторской диссертации великого физика А. Эйнштейна было определение взаимосвязи между параметрами дисперсной фазы и вязкостью суспензии в целом. Он получил следующий ре - зультат:
т! = n<, О + к • Ф),
где н0 — вязкость дисперсионной среды: Ф — объемная концентрация частиц; к — коэффициент, равный 2,5, для твердых сферических частиц [Charm S., Kurland G., 1974].
Формула А. Эйнштейна выведена для объемной концентрации частиц не более 1 %, од - нако некоторые авторы при оценке зависимости вязкости крови от гематокритного числа ссьшаются на удовлетворительные результаты расчетов с ее использованием [Charm S., Kurland G., 1974].
Пользуется популярностью соотношение Тейлора для эмульсии сферических жидких частиц:
Л = По (1 + Ф • ТГ2'\
где TI0 — вязкость дисперсионной среды; Ф — объемная концентрация частиц; Т — коэффициент Тейлора, равный (Р+0,4)/(Р+1,0); Р = Т1р/г|о; ц10 — вязкость жидких частиц, в данном случае «внутренняя» вязкость эритроцитов [Dintenfass L., 1971].
Существует множество аналогичных уравнений, общим для которых является наличие связи между объемной концентрацией частиц и вязкостью среды в целом, а также возраста - ние роли фактора взаимодействия между частицами на текучесть дисперсной фазы.
С.А. Регирер (1982) приводит формулы для расчета вязкости крови и предела ее текучести с использованием гематокритного числа:
71 « ло (1 - к • НГ2-5,
где 0,8;
вязкость плазмы; к — коэффициент, равный для эритроцитов здорового человека
т0 « А • с2 (Ф - 0,05)3,
где т0 — предел текучести; с — концентрация фибриногена.
Вместе с тем автор указывает, что параметры к и с существенно зависят от температуры, деформируемости эритроцитов, видовой принадлежности крови.
Одним из результатов докторской диссертации известного специалиста в области гемо - реологии G. Cokelet (1963) было выведение следующей зависимости:
498
Рекомендовано к покупке и изучению сайтом МедУнивер - https://meduniver.com/

1 (1 - D)2'3'
где r| — вязкость крови; л0 — вязкость плазмы; D — диаметр клеток.
S. Charm, G. Kurland (1974) в свою очередь предлагают использовать для крови следующее соотношение:
г, - 0,07ехр(2,49 • Н + -М^ехр - 1,69 • Н).
Автор, предлагая эту формулу, сравнивает ее с формулой А. Эйнштейна (не имеющей к крови никакого отношения) и утверждает, что результаты расчетов по обеим формулам не отличаются друг от друга более чем на 10 %.
Заслуживает внимания предложение J. Fung (1981) использовать для расчета вязкости крови в капиллярах специальное уравнение:
где т)0 — вязкость плазмы; С — постоянная величина (например, для легочных капилляров
1,16).
Из приведенных сведений становится очевидным, что наличие зависимости вязкости крови от гематокритного числа сомнений не вызывает. Между тем на практике нередки случаи, когда значительная гемоконцентрация не сопровождается увеличением вязкости. Нами наблюдался больной с полицитемией, у которого, несмотря на колебания гематокритного числа от 0,60 до 0,69, текучесть крови оставалась в пределах нормы. Этот факт, а также оби - лие различных уравнений для расчета вязкости крови с использованием гематокритного числа свидетельствуют, по-видимому, о том, что для каждого патологического процесса, а зачастую и для его отдельных фаз или периодов существует определенная (индивидуальная) зависимость г\ ~ Н. Наши многолетние наблюдения показывают, что в целом связь между гематокритным числом и вязкостью тем отчетливее, чем в большей степени этот показатель уклоняется от границ нормы в ту или другую сторону.
Кроме того, установлено, что степень влияния концентрации эритроцитов на текучесть крови зависит от градиента скорости, поскольку при разных скоростях деформации факторы взаимодействия эритроцитов (ориентационные эффекты и агрегация) также выражены не - одинаково.
Гемодинамические факторы. Гемодинамика — процесс механического перемещения крови по системе кровообращения, включающей в себя комплекс специфических анатоми - ческих структур и регуляторных механизмов. Движение крови определяется: 1) пропульсивной способностью сердца; 2) функциональным состоянием кровеносного русла; 3) свойства - ми самой крови. Несмотря на то что способность крови течь по сосудам обусловлена слож - ными электрофизиологическими, биохимическими и коллоидно-осмотическими явлениями, для гемодинамики важнейший интерес представляют реологические свойства движущейся крови, являющиеся своего рода интегральными ее параметрами. Отличительной особеннос - тью реологических свойств крови как параметров гемодинамики является то, что они в оди - наковой мере определяют как системную гемодинамику (наряду с артериальным давлением, частотой сердечных сокращений и т. д.), так и микрогемоциркуляцию. Вместе с тем реологические свойства крови принципиально по-разному реализуются в различных участках сосудистого русла (крупных сосудах и сосудах зоны микрогемоциркуляции).
Основной реологический параметр крови — ее текучесть — является функцией скорости деформации, которая в свою очередь определяется размерами сосуда и скоростью кровотока в нем. Это объясняет, почему эффективная вязкость крови может быть неодинаковой в сосудах различного диаметра.
В то же время достаточно точное определение градиентов скорости в различных отделах системы кровообращения — задача далеко не простая. Трудности имеют двоякий характер. С одной стороны, невозможно однозначно определить геометрические параметры сосудов и характеристики кровотока, необходимые для расчета скоростей деформации, с другой стороны, есть принципиальная трудность, суть которой состоит в том, что градиент скорости при условии течения по сосудам является функцией текучести крови. Таким образом, при реше - нии задачи определения скоростей деформации в различных отделах сосудистого русла возникает порочный круг.
32* |
499 |
|
