2. Метод эквивалентного источника тока

С помощью метода эквивалентного источника тока определить комплексный ток в сопротивлении R₂. Произвольно выбираем положительное направление искомого тока I₃ в ветви на исходной схеме 1 (рис. 17):

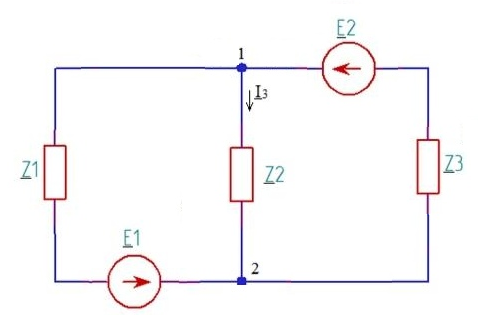
Рисунок - 17

Составляем схему 2 (рис.18), заменив ветвь короткозамкнутым отрезком. Направление тока короткого замыкания I_k выбираем совпадающим с направлением тока I₃:

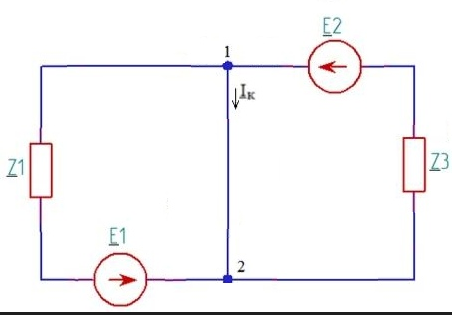
Рисунок - 18

Вычисляем ток I_k1 и I_k2 методом наложения и составляем равенство:

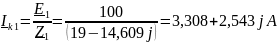
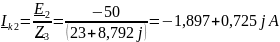
Составляем схему 3 (рис.19) для вычисления Z_ЭК. Для этого используем схему 2, в которой источники ЭДС заменяют короткозамкнутыми отрезками:

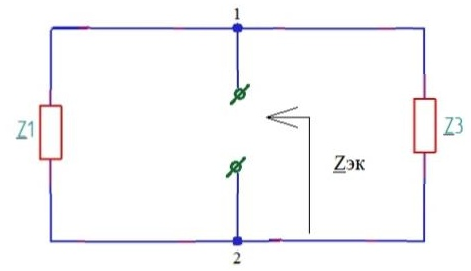
Рисунок - 19

Используя эквивалентные преобразования, вычисляем Z_ЭК относительно зажимов:

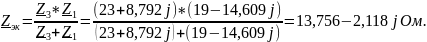
Составим цепь (рис.20). При этом направление J_ЭК на схеме 4 должно быть противоположным направлению I_k в схеме 2:

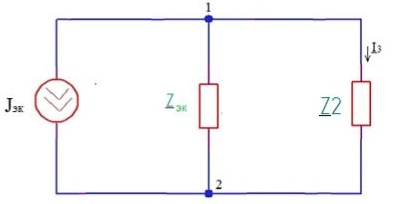
Рисунок - 20

Используя метод уравнений Кирхгофа, находим искомый ток:

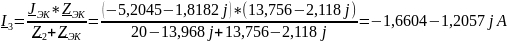
Ответ:

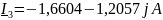
2. Баланс комплексных мощностей

Исходная электрическая цепь представлена на рис.21:

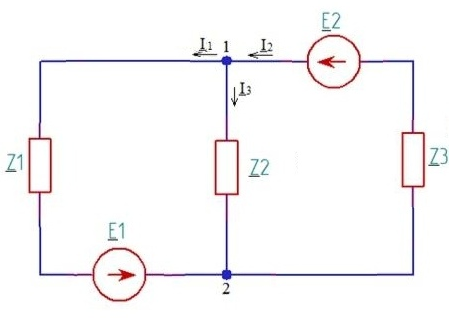
Рисунок – 21

Рассчитанные комплексные токи:

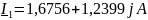
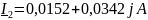
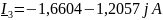
Задаем значения комплексно сопряженных токов:

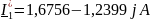
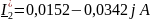
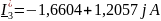
Вычислим мощность источников по формуле с помощью программы Mathcad:

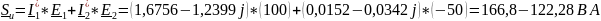
Вычислим мощность, расходуемую в приемниках, по формуле с помощью программы Mathcad:

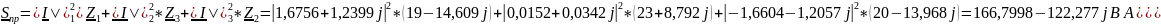
Рассчитываем относительную погрешность действительной части баланса мощностей:

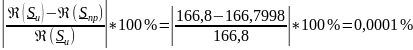
Рассчитываем относительную погрешность мнимой части баланса мощностей:

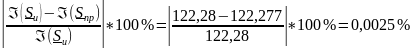
Таким образом, баланс активной мощности сошелся с точностью 0,0001%, а баланс реактивной мощности с точностью 0,0025%.

Отобразим значения мощностей действительной (рис.22) и мнимой (рис.23) частей на диаграммах:

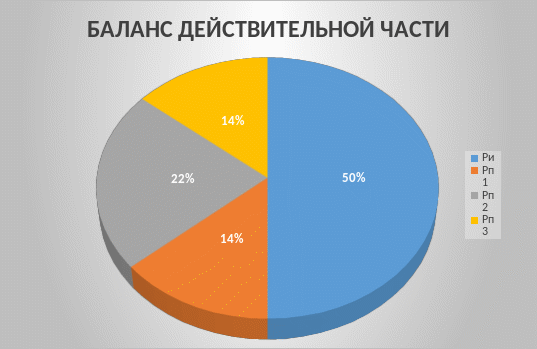
Рисунок - 22

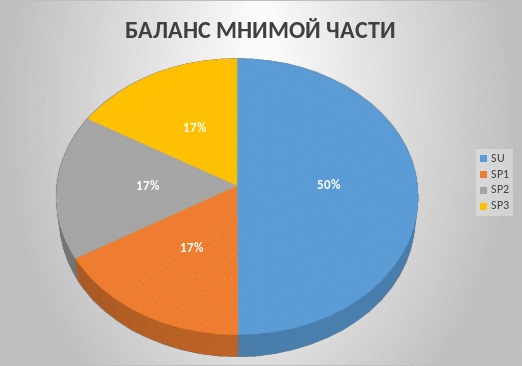
Рисунок - 23

Заключение

В данной курсовой работе были применены методы для расчета комплексных токов такие как: метод уравнений Кирхгофа для комплексных величин, метод контурных токов для комплексных величин, узловых потенциалов для комплексных величин, метод двух узлов для комплексных величин, метод наложения для комплексных величин, метод эквивалентного генератора ЭДС для комплексных величин, метод эквивалентного генератора тока для комплексных величин.

Методами уравнения Кирхгофа, контурных токов, узловых потенциалов, двух узлов и наложения для комплексных величин были найдены все три комплексных тока в цепи.

Метод эквивалентного генератора ЭДС для комплексных величин был найден ток I₁.

Метод эквивалентного источника тока для комплексных величин был найден ток I₃.

В каждом методе значения комплексных токов совпали.

Баланс активной мощности сошелся с точностью 0,0001%, а баланс реактивной мощности с точностью 0,0025%.

Список используемых источников

1. Фриск В.В. ОТЦ. Сборник задач с примерами применения персонального компьютера –М.: СОЛОН-Пресс, 2003. –192 с.

2. Фриск В.В. Основы теории цепей. –М.: РадиоСофт, 2002. –288 с.

3. Фриск В.В. ОТЦ. Лабораторный практикум на персональном компьютере –М.: СОЛОН-Пресс, 2002. –192 с.

4. Фриск В.В. ОТЦ. Расчеты и моделирование с помощью пакета компьютерной математики Mathcad. – М.: СОЛОН-Пресс, 2006. – 88 с.

5. Шебес М.Р., Каблукова М.В. Задачник по теории линейных электрических цепей. –М.: Высшая школа, 1990. – 5-50, 50-90 с.

6. Фриск В.В., Репинский В.Н., Смирнов Н.И. Методические указания по использованию ЭВМ в курсовом проектировании по курсу ТЭЦ. Часть 1. –М.: МТУСИ, 1991. –28 с.

7. http://www.mt-system.ru/store/12262/rezistory-raznye

8. http://frisk.ucoz.com/

9. https://www.chipdip.ru/product1/8319251542?from=suggest_product

10. http://www.hitano.com.tw/

11. Бычков Ю.А., Золотницкий В.М., Чернышев Э.П. и др. Сборник задач и практикум по основам теории электрических цепей. - СПб.: Питер, 2005. Новгородцев А.Б. Теоретические основы электротехники. 30 лекций по теории электрических цепей. Учебное пособие. 2-е издание. - СПб.: Питер, 2006.

12. Шебес М.Р., Каблукова М.В. Задачник по теории линейных электрических цепей. –М.:Высшая школа, 1990.

13. Шнеперман, Л.Б. Основы теории цепей: Учебник / Л.Б. Шнеперман. - СПб.: Лань, 2009.

14. Шакин В.Н., Семенова Т.И., Фриск В.В. Базовые средства математического пакета Scilab. Учебник для вузов, 2019.