ФЕДЕРАЛЬНОЕ АГЕНСТВО СВЯЗИ

Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования

Московский технический университет связи и информатики

(МТУСИ)

Кафедра Теории электрических цепей

Курсовая работа

«Расчёт резистивных цепей постоянного тока»

Выполнил студент группы БЭИ2203 Малых Д. С.

Проверил доц. кафедры ТЭЦ Кириллов Д. В.

Москва 2023

Содержание

Обозначения и сокращения………………………………………………………4

Введение…………………………………………………………………………..5

1 Расчет резистивных цепей постоянного тока…………………………………6

1.1 Параметры элементов схемы ………………………………………………...6

1.2 Метод уравнений Кирхгофа…………………………………………………6

1.3 Метод контурных токов………………………………………………………9

1.4 Метод узловых потенциалов………………………………………………11

1.5 Метод двух узлов……………………………………………………………12

1.6 Метод наложения……………………………………………………………14

1.7 Метод эквивалентного источника ЭДС ……………………………………17

1.8 Метод эквивалентного источника тока………………….……….………...20

1.9 Расчет баланса мощностей…….……………………………………………23

Заключение………………………………………………………………………26

Список используемых источников….…………………………….……………27

Обозначения и сокращения

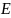– ЭДС, В

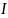– Сила тока, A

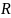– Сопротивление, Ом

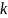– число независимых контуров

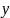– число уравнений

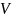– потенциал, В

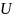– Напряжение, В

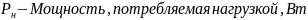
Ny - число узлов

Nв – число ветвей

Nт – число токов

R11 – собственное сопротивление 1-го контура;

R22 – собственное сопротивление 2-го контура;

R12=R21 – общее сопротивление 1-го и 2-го контуров;

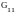- сумма проводимостей ветвей, присоединенных к первому узлу;

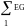- алгебраическая сумма произведений ЭДС ветвей, примыкающих к 1-ому узлу, на их проводимость;

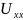– напряжение холостого хода, В

1. Расчет резистивных цепей постоянного тока

   1. Параметры элементов схемы:

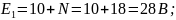
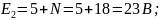
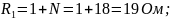
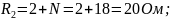
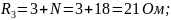
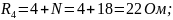
N = 18.

Исходная схема представлена на рис. 2:

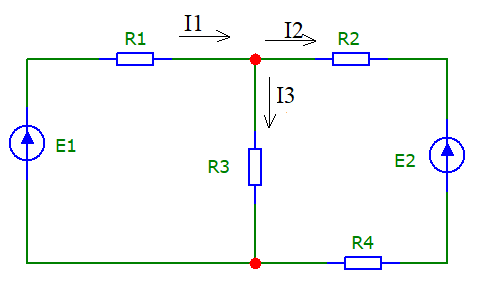
Рисунок - 2

2. Метод уравнения Кирхгофа

С помощью метода уравнений Кирхгофа определим токи во всех ветвях.

Для использования данного метода необходимо произвольно задать

направление токов во всех ветвях, что продемонстрировано на рис.3:

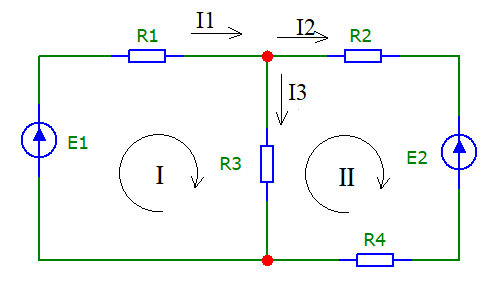
Рисунок - 3

Выбираем произвольно положительные направления токов во всех ветвях и рассчитываем необходимое количество уравнений по первому и второму законам Кирхгофа:

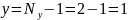
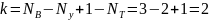
Запишем уравнение по 1-ому закону Кирхгофа:

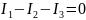
Для записи уравнений по 2-ому закону Кирхгофа произвольно выбираем первый контур и в нем произвольно задается направление обхода контура. Затем из цепи мысленно удаляется какая-либо ветвь (для обеспечения независимости уравнений во 2-ом законе Кирхгофа друг от друга) и снова задается направление обхода для оставшегося участка.

Для каждого контура записываются уравнения по 2-ому закону Кирхгофа:

Составляем систему уравнений и решаем ее:

Представим систему в матричном виде:

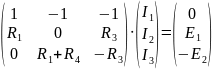
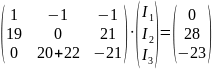
или

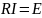
Далее находим токи:

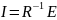
Вычисление токов было произведено с помощью программы MATHCAD:

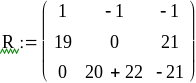
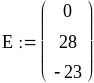
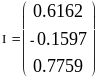
А

А

А

Ответ:

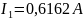
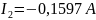
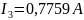
3. Метод контурных токов

С помощью метода контурных токов определим токи во всех ветвях.

Произвольно выбрать направления всех токов в ветвях на исходной

схеме (рис.4)

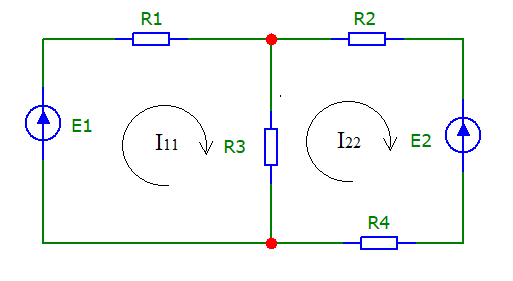
Рисунок - 4

Число независимых контуров:

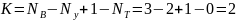
Выбираем положительные направления для контурных токов

,

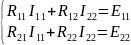где

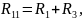
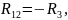
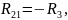
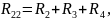
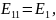
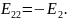
Выпишем систему уравнений еще раз

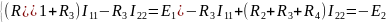
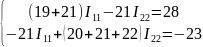
Вычисление токов было произведено с помощью программы MATHCAD:

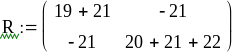
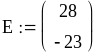
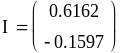
А

А

А

Ответ:

4. Метод узловых потенциалов

С помощью метода узловых потенциалов определим токи во всех ветвях.

Произвольно выбираем направление всех токов в ветвях на исходной схеме (рис.5)

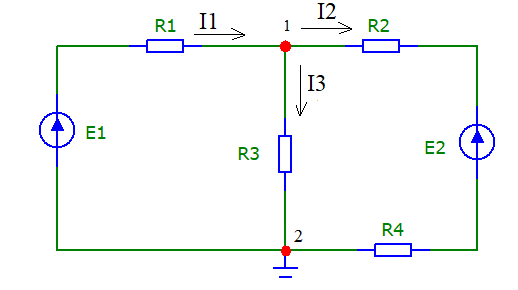
Рисунок - 5

Число уравнений:

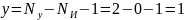
Принимаем потенциал узла 2 равен нулю: 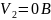. Тогда составим уравнение для нахождения потенциала узла 1:

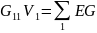
Где 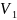– потенциал узла 1;

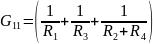- сумма проводимостей ветвей, сходящихся в узле 1;

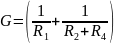- сумма проводимостей ветвей, непосредственно соединяющих узел 1 с узлом 2;

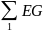– алгебраическая сумма произведения ЭДС ветвей, примыкающих к узлу 1, на их проводимости.

С помощью программы Mathcad находим:

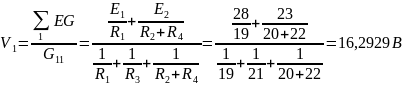
Найдя потенциал V₁ подставим его в уравнения для токов и получим значения всех токов с помощью программы Mathcad Prime. Токи в ветвях, согласно обобщенному закону Ома, при V₂=0 В равны:

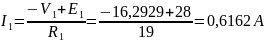
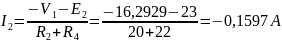
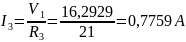
Ответ:

5. Метод двух узлов

С помощью двух узлов определим токи во всех ветвях.

Метод двух узлов является частным случаем метода узловых потенциалов и наиболее рационален для расчёта цепей, содержащих два узла. Для расчёта методом двух узлов находят напряжение между этими узлами U₁₂. Нужно определить напряжение между двух узлов и рассчитать исходя из этого все токи в ветвях. Схема с учётом данного метода представлена на:

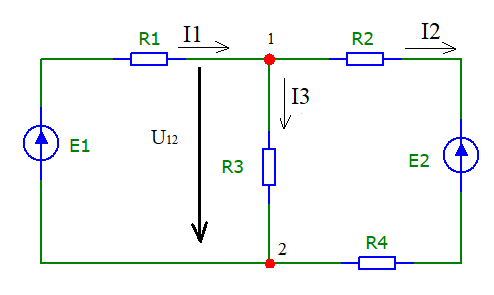
Рисунок - 6

Примем потенциал узла 2 равным нулю V₂=0 В. Тогда напряжение U₁₂ будет направлено из точки с большим потенциалом, к точке с меньшим.

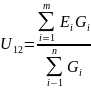
Где

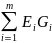- алгебраическая сумма произведения ЭДС ветвей, примыкающих к узлу 1, на их проводимости;

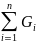- алгебраическая сумма проводимостей всех ветвей схемы.

Определяем напряжение U₁₂ между узлами по формуле:

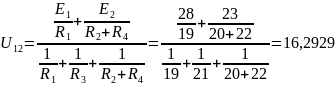В

Знак ЭДС определяется ее направлением. Если к узлу, то отрицательное, если от узла - положительное.

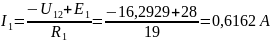
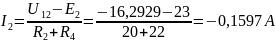
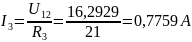
Ответ: ; ;