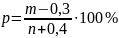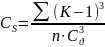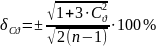3.2 Определение параметров кривой обеспеченности , ,
Средний многолетний расход вычисляется по формуле:
|
(3.1) |
где
– сумма среднемесячных расходов за 50
лет, (
);
– период
наблюдений (количество лет),
;
Модульные коэффициенты K:
|
(3.2) |
где
– соответствующее значение расхода,
за период наблюдений.
Для проверки вычислений следует помнить, что сумма значений «К» должна равняться общему числу членов ряда :
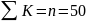
Далее
вычисляют отклонения от середины
.
Для проверки: сумма
должна быть равна нулю. Затем подсчитывают
и
.
Контроль построения теоретической кривой обеспеченности расходов выполняется следующим образом:
|
(3.3) |
где
– порядковый номер члена ряда;
– общее число членов ряда.
Коэффициент вариации вычисляется по формуле:
|
(3.4) |
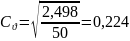
Коэффициент асимметрии вычисляется по формуле:
|
(3.5) |
3.3 Вычисление средней квадратической ошибки определения
Средняя квадратическая ошибка определения коэффициента вариации вычисляется по формуле:
|
(3.6) |
Допустимая ошибка равна 10,84%.
Средняя квадратическая ошибка коэффициента асимметрии вычисляется по формуле:
|
(3.7) |
,
Допустимая ошибка равна 92%.
3.4 Вычисление и построение фактической и теоретической кривых обеспеченности среднемноголетних расходов
Зная
величины параметров
,
и
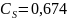вычисление
теоретической кривой обеспеченности
средних годовых расходов производят
по таблице 10 С.И. Рыбкина – П.А. Алексеева
(Приложение 3), в которой даны относительные
отклонения от середины ординат
интегральной кривой при
и разных процентах обеспеченности
.
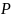По
данным таблицы 10 определяют значения
ординат
при
и
записывают их во вторую строку таблицы
3 (строка
).
Таблица 3 – Данные для вычисления теоретической кривой обеспеченности среднемноголетних расходов реки Марха
P, % |
1,00 |
3,00 |
5,00 |
10,00 |
20,00 |
50,00 |
75,00 |
90,00 |
95,00 |
97,00 |
99,00 |
99,90 |
Ф |
2,80 |
2,15 |
1,82 |
1,33 |
0,79 |
-0,12 |
-0,72 |
-1,18 |
-1,43 |
-1,58 |
-1,82 |
-2,17 |
Ms=Ф*Cv |
0,63 |
0,48 |
0,41 |
0,30 |
0,18 |
-0,03 |
-0,16 |
-0,26 |
-0,32 |
-0,35 |
-0,41 |
-0,48 |
Ks=Ms+1 |
1,63 |
1,48 |
1,41 |
1,30 |
1,18 |
0,97 |
0,84 |
0,74 |
0,68 |
0,65 |
0,59 |
0,52 |
Q=Ks*Qср |
658,67 |
599,22 |
569,35 |
525,39 |
476,51 |
394,54 |
339,83 |
297,79 |
275,67 |
262,09 |
239,97 |
208,90 |
Вычисление теоретической кривой обеспеченности средних годовых расходов воды р. Марха при , и
.
В
виду того, что отклонения кривой от
середины пропорциональны
,
все значения
умножаются на
с точностью до тысячных (строка 3 табл.
3).
В
таблице 3 значения
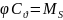указывают отклонения ординат кривой
от среднего значения ряда, которое
принято равным единице, поэтому при
определении модульных коэффициентов
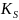для построения кривой обеспеченности
прибавляется единица (строка 4:
.
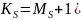Чтобы
найти расход Q,
соответствующий каждой величине заданной
(вычисляемой) обеспеченности Р,
необходимо значение
для построения кривой обеспеченности
умножить на Qср
= 405 м3/с.
Откладывая
по оси ординат значения, приведённых
средних годовых расходов Q,
из строки 5
(табл. 3), а по оси абсцисс соответствующие
проценты обеспеченности, получают
точки, по которым и проводят кривую,
называемую теоретической кривой
обеспеченности расходов (рис.3), построенную
в простых координатах. Её недостаток в
следующем: она имеет верхнюю и нижнюю
ветви кривой с крутыми подъёмами, где
малым приращениям абсцисс соответствуют
большие приращения ординат, что не
позволяет достаточно точно снимать
значения
.
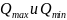Кривые обеспеченности представлены на рисунке 3.
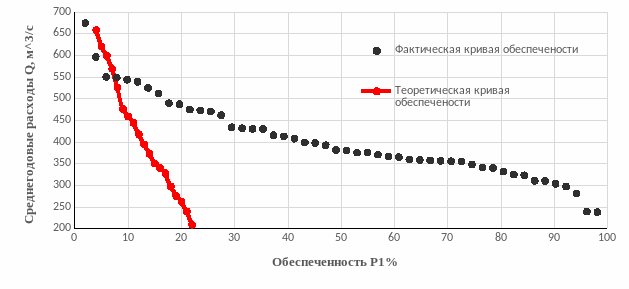
Рисунок 3 – кривые обеспеченности среднемноголетних расходов реки Марха