1-й Семестр Механика / 3 / «Определение момента инерции тела, скатывающегося по наклонной поверхности»

Министерство образования и науки РФ

Федеральное государственное автономное образовательное учреждение

высшего профессионального образования

«Сибирского Федерального Университета»

Саяно-Шушенский филиал

Отчет по лабораторной работе № 4.

«Определение момента инерции тела, скатывающегося по наклонной поверхности».

Выполнил: студент группы ГЭ14-03Б

Проверил: старший преподаватель

кафедры ФП:

Глушенкова Елена Александровна

г. Саяногорск

Цель: определить момент инерции тела относительно мгновенной оси враще­ния расчётным и экспериментальным методом.

Оборудование: установка, набор тел, секундомер.

Схема экспериментальной установки:

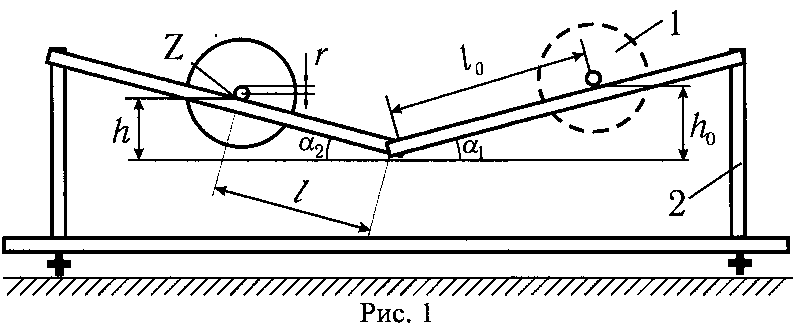
Рабочие формулы:

формула для определения момента инерции динамическим методом:

,где I – момент инерции скатывающегося тела, _кг*м2

m – масса тела, включающая в себя массу стержня;

g – ускорение свободного падения (=9,81 м²/с);

l – путь, пройденный телом, поднимающимся по инерции до остановки;

r – радиус оси вращения, где осью является цилиндрический стержень;

(α1 +α2 ) – сумма углов наклонных поверхностей;

t– время движения от верхней точки до нижней;

l0 – путь, пройденный телом от верхней точки до нижней.

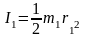
_{, где – момент инерции тела, кг*м2;}

m – масса вращающегося диска;

r – радиус оси вращения;

Ход работы:

1. результаты эксперимента

Таблица 1. Расчёт момента инерции тела сложной формы

№ п.п.	Элемент тела вращения	Масса m, кг	Диаметр d, м и а, м	Момент инерции I, кг м2
				формула	значение
1	Диск	0.395	D=0.16 r1=0.0045		3.99*10-6

Таблица 2. Определение момента инерции тела динамическим методом

№ п.п.	d, м	t, c	l, м	(α1+α2) = 0.25 рад M = 0.867 кг l0 = 0.38 м r = /2 = 0.0045 м
1	0.009	10.1	0.195
2	0.009	10.5	0.18
3	0.009	10.2	0.185
4	0.009	9.7	0.18
5	0.009	9.8	0.18
Среднее значение	0.009	10.06	0.184	I=2.07*10-3 кг·м2

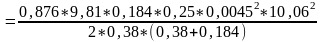=2.076*10-3кг*м2

Таблица 3. Изучение зависимости момента инерции от распределения массы относительно оси вращения

№	b, см.	t, c	l, м	b2, см2	I,кг м2	(α1+α2) = 0.25 рад m = 0.49 кг l0 = 0.38 м r = /2= 0.0045 м
1	7	10	0.24	49	1.24*10-3
2	6	9	0.25	36	1.03*10-3
3	5	8.6	0.23	25	0.87*10-3

Вывод: В результате проделанной работы была вычислена инерция вращающегося диска относительно МОВ(I_д=2.07*10^-3 кг·м²), динамическим методом, из данных таблицы 3 вычислили момент инерции крестовины и массу грузов(I₀=0,57*10^-3кг*м³;m=75г). Также выяснили, что момент инерции вращающегося тела прямо пропорционален квадрату расстояния от оси до груза

Министерство образования и науки РФ

Федеральное государственное автономное образовательное учреждение

высшего профессионального образования

«Сибирского Федерального Университета»

Саяно-Шушенский филиал

Отчет по лабораторной работе № 4.

«Определение момента инерции тела, скатывающегося по наклонной поверхности».

Выполнил: студент группы ГЭ14-03Б

Тимофеева Наталья

Проверил: старший преподаватель

кафедры ФП:

Глушенкова Елена Александровна

г. Саяногорск

Цель: определить момент инерции тела относительно мгновенной оси враще­ния расчётным и экспериментальным методом.

Оборудование: установка, набор тел, секундомер.

Схема экспериментальной установки:

Рабочие формулы:

формула для определения момента инерции динамическим методом:

,где I – момент инерции скатывающегося тела, _кг*м2

m – масса тела, включающая в себя массу стержня;

g – ускорение свободного падения (=9,81 м²/с);

l – путь, пройденный телом, поднимающимся по инерции до остановки;

r – радиус оси вращения, где осью является цилиндрический стержень;

(α1 +α2 ) – сумма углов наклонных поверхностей;

t– время движения от верхней точки до нижней;

l0 – путь, пройденный телом от верхней точки до нижней.

_{, где – момент инерции тела, кг*м2;}

m – масса вращающегося диска;

r – радиус оси вращения;

Ход работы:

2. результаты эксперимента

Таблица 1. Расчёт момента инерции тела сложной формы

№ п.п.	Элемент тела вращения	Масса m, кг	Диаметр d, м и а, м	Момент инерции I, кг м2
				формула	значение
1	Диск	0.395	D=0.16 r1=0.0045		3.99*10-6

Таблица 2. Определение момента инерции тела динамическим методом

№ п.п.	d, м	t, c	l, м	(α1+α2) = 0.25 рад M = 0.867 кг l0 = 0.38 м r = /2 = 0.0045 м
1	0.009	10.1	0.195
2	0.009	10.5	0.18
3	0.009	10.2	0.185
4	0.009	9.7	0.18
5	0.009	9.8	0.18
Среднее значение	0.009	10.06	0.184	I=2.07*10-3 кг·м2

=2.076*10-3кг*м2

Таблица 3. Изучение зависимости момента инерции от распределения массы относительно оси вращения

№	b, см.	t, c	l, м	b2, см2	I,кг м2	(α1+α2) = 0.25 рад m = 0.49 кг l0 = 0.38 м r = /2= 0.0045 м
1	7	10	0.24	49	1.24*10-3
2	6	9	0.25	36	1.03*10-3
3	5	8.6	0.23	25	0.87*10-3

Вывод: В результате проделанной работы была вычислена инерция вращающегося диска относительно МОВ(I_д=2.07*10^-3 кг·м²), динамическим методом, из данных таблицы 3 вычислили момент инерции крестовины и массу грузов(I₀=0,57*10^-3кг*м³;m=75г). Также выяснили, что момент инерции вращающегося тела прямо пропорционален квадрату расстояния от оси до груза

Контрольные вопросы

1. В начале движения потенциальная энергия максимальна, кинетическая равна 0.

В конце движения потенциальная энергия снова достигает максимума, но меньшего чем в начале движения, а кинетическая энергия равна 0.

В нижней точке кинетическая энергия максимальна, а потенциальная энергия равна 0. В произвольной точке при скатывании потенциальная энергия убывает, а кинетическая увеличивается.

2. Поступательно вращательный характер движения по направляющим. Сила тяжести создает момент относительно оси вращения.

3. Угловая скорость тела

,

где t - время движения от верхней точки до нижней, r - радиус стержня (оси).

4. ля определения угловой скорости определяют в нижней точке скорость поступательного движения центра масс , где t - время движения от верхней точки до нижней.

На скатывающееся тело действует момент сил сопротивления М_тр.

Работа его на пути l₀ равна A = М_трφ где угловой путь φ = l₀/r.

5. Формула для определения момента инерции динамическим методом:

Здесь величина (α₁ и α₂) является константой для данной установки.

Момент инерции тела относительно MOB определяется теоремой Штейнера J = J₀ + ma²,

где J₀ - момент инерции, относительно центра масс; а - расстояние от центра масс тела до оси вращения.

6. Исследование формы тела. Принимая во внимание, что момент инерции любо­го тела равен сумме моментов инерции отдельных его элементов, мысленно разделяя исследуемое тело на простые элементы.

Сделать эскиз исследуемого тела, а если необходимо, то и его элемен­тов, обозначая символами все размеры, подлежащие измерению.

7. Источник систематических погрешностей при измерениях - приборная погрешность, равная цене деления измерительного прибора. Случайная погрешность определяется по разбросу выборки:

∆=(Х_max-X_min)/2

т.е. проводится несколько повторных измерений и находится среднее значение величины.