chertov / Глава 8. Физика атомного ядра и элементарных частиц / 41_Радиоактивность

41. РАДИОАКТИВНОСТЬ.

Основные формулы

• Основной закон радиоактивного распада

N=N₀e^-λt

где N — число нераспавшихся атомов в момент времени t; N₀— число нераспавшихся атомов в момент, принятый за начальный (при t=0); е — основание натуральных логарифмов; λ — постоян­ная радиоактивного распада.

• Период полураспада T_1/2 — промежуток времени, за который число нераспавшихся атомов уменьшается в два раза. Период полу­распада связан с постоянной распада соотношением

T_1/2 = ln2/λ = 0,693/λ .

• Число атомов, распавшихся за время t,

∆N = N₀ - N = N₀, (1 - е^-λt).

Если промежуток времени ∆t << T_1/2. то для определения числа распавшихся атомов можно применять приближенную формулу

∆N ≈ λN∆t

Среднее время жизни т радиоактивного ядра — промежуток времени, за который число нераспавшихся ядер уменьшается в е раз:

τ = 1/λ

• Число атомов, содержащихся в радиоактивном изотопе,

N = (m/M)N_A

где m — масса изотопа; М — его молярная масса; N_A — постоян­ная Авогадро.

• Активность А нуклида в радиоактивном источнике (актив­ность изотопа) есть величина, равная отношению числа dN ядер, распавшихся в изотопе, к промежутку времени dt, за которое произошел распад. Активность определяется по формуле

A = -dN/dt = λN,

или после замены N по основному закону радиоактивного распада

A = λN₀e^-λt

Активность изотопа в начальный момент времени (t=0)

A₀ = λN₀ .

Активность изотопа изменяется со временем по тому же закону, что и число нераспавшихся ядер:

A = A₀e^-λt

• Массовая активность а радиоактивного источника есть вели-

чина, равная отношению его активности A к массе т этого источни­ка, т. е.

a = A/m.

● Если имеется смесь ряда радиоактивных изотопов, образую­щихся один из другого, и если постоянная распада λ первого члена ряда много меньше постоянных всех остальных членов ряда, то в смеси устанавливается состояние радиоактивного равновесия, при котором активности всех членов ряда равны между собой:

λ₁N₁ = λ₂N₂ = … = λ_kN_k.

Примеры решения задач

Пример 1. Определить начальную активность А₀ радиоактив­ного магния ²⁷Mg массой m=0,2 мкг, а также активность А по исте­чении времени t=1 ч. Предполагается, что все атомы изотопа ра­диоактивны.

Решение. Начальная активность изотопа

А₀ = λN₀ (1)

где λ — постоянная радиоактивного распада; N₀— количество ато­мов изотопа в начальный момент (t=0).

Е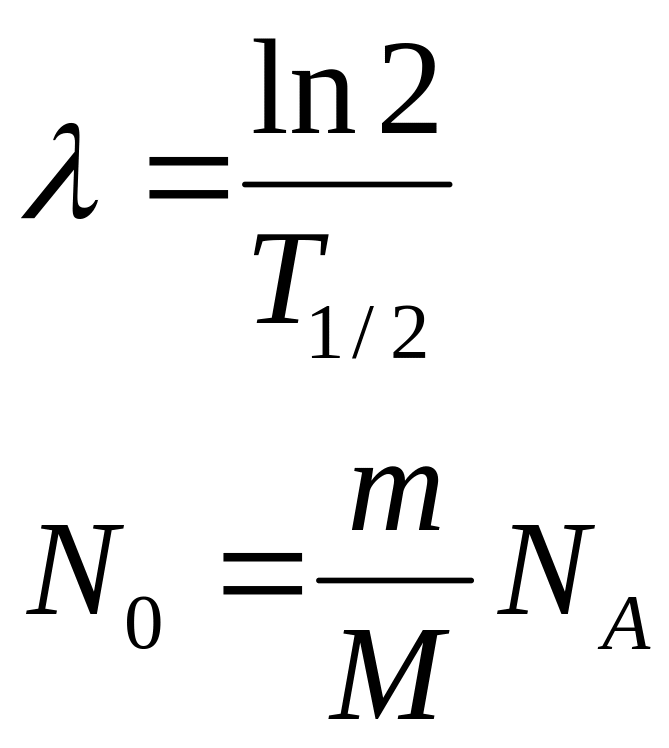 сли учесть, что

то формула (1) примет вид

В ыразим входящие в эту формулу величины в СИ и произведем вычисления:

A₀=5,1510¹² Бк=5,15ТБк.

Активность изотопа уменьшается со временем по закону

A=A₀ e^-λt (3)

Заменив в формуле (3) постоянную распада λ ее выражением, по­лучим

A=A₀ e^-ln2*t/T1/2 =A₀ (e^ln2)^-t/T1/2

Так как e^ln2 = 2 окончательно будем иметь

A=A₀ /2^t/T1/2

Сделав подстановку числовых значений, получим A=8,0510¹⁰ Бк=80,5 ГБк .

Пример 2. При определении периода полураспада T_1/2 короткоживущего радиоактивного изотопа использован счетчик импульсов. За время ∆t = 1 мин в начале наблюдения (t=0) было насчитано ∆n₁=250 импульсов, а по истечении времени t=1 ч—∆n₂=92 импуль­са. Определить постоянную радиоактивного распада λ и период полураспада T_1/2 изотопа.

Решение. Число импульсов ∆n, регистрируемых счетчиком за время ∆t, пропорционально числу распавшихся атомов ∆N.

Таким образом, при первом измерении

∆n₁=k∆N₁=kN₁(1-e^–λ∆t), (1)

где N₁— количество радиоактивных атомов к моменту начала от­счета; k — коэффициент пропорциональности (постоянный для данного прибора и данного расположения прибора относительно радиоактивного изотопа).

При повторном измерении (предполагается, что расположение приборов осталось прежним)

∆n₂=k∆N₂=kN₂(1-e^–λ∆t), (2)

где N₂— количество радиоактивных атомов к моменту начала вто­рого измерения.

Разделив соотношение (1) на выражение (2) и приняв во внима­ние, что по условию задачи ∆t одинаково в обоих случаях, а также что N₁ и N₂. связаны между собой соотношением N₂ = N₁ e^-λt, по­лучим

∆n₁/∆n₂=e^λt (3)

где t — время, прошедшее от первого до второго измерения. Для вы­числения  выражение (3) следует прологарифмировать: In(∆n₁/∆n₂)=λt, откуда

λ = (1/t)ln(∆n₁/∆n₂).

Подставив числовые данные, получим постоянную радиоактив­ного распада, а затем и период полураcпада:

λ = (1/1)ln(250/92)ч^-1 = 1ч^-1;

T_1/2 = ln2/λ = 0,693/1 = 0,693ч = 41,5 мин.

Задачи

Закон радиоактивного распада

41.1. Какова вероятность W того, что данный атом в изотопе ра­диоактивного йода ¹³¹I распадается в течение ближайшей секунды?

41.2. Определить постоянные распада λ изотопов радия ²¹⁹₈₈Ra и

²²⁶₈₈Ra.

41.3. Постоянная распада λ рубидия ⁸⁹Rb равна 0,00077 c^-1. Определить его период полураспада T_1/2.

41.4. Какая часть начального количества атомов распадется за один год в радиоактивном изотопе тория ²²⁸Th?

41.5. Какая часть начального количества атомов радиоактивного актиния ²²⁵Ас останется через 5 сут? через 15 сут?

41.6. За один год начальное количество радиоактивного изотопа уменьшилось в три раза. Во сколько раз оно уменьшится за два года?

41.7. За какое время t распадается ¼ начального количества ядер радиоактивного изотопа, если период его полураспада Т_1/2=24 ч?

41.8. За время t=8 сут распалось k= ¾ начального количества ядер радиоактивного изотопа. Определить период полураспада T_1/2.

41.9. При распаде радиоактивного полония ²¹⁰Ро в течение вре­мени t= 1ч образовался гелий ⁴Не, который при нормальных усло­виях занял объем V=89,5 см³. Определить период полураспада T_1/2 полония.

41.10. Период полураспада T_1/2 радиоактивного нуклида равен 1 ч. Определить среднюю продолжительность т жизни этого нуклида.

41.11. Какая часть начального количества радиоактивного нук­лида распадается за время t, равное средней продолжительности τ жизни этого нуклида?

Активность. Радиоактивное равновесие

41.12. Определить число N атомов, распадающихся в радиоактив­ном изотопе за время t=10 с, если его активность A=0,1 МБк. Считать активность постоянной в течение указанного времени.

41.13. Активность А препарата уменьшилась в k=250 раз. Скольким периодам полураспада T_1/2 равен протекший промежуток времени t?

41.14. За время t=1сут активность изотопа уменьшилась от A₁=118 ГБк до A₂=7,4 ГБк. Определить период полураспада T_1/2 этого нуклида.

41.15. На сколько процентов снизится активность А изотопа иридия ¹⁹²Ir за время t=30 сут?

41.16. Определить промежуток времени τ, в течение которого активность А изотопа стронция ⁹⁰Sr уменьшится в k₁=10 раз? в k₂= 100 раз?

41.17. Счетчик Гейгера, установленный вблизи препарата ради­оактивного изотопа серебра, регистрирует поток β-частиц. При пер­вом измерении поток Ф₁ частиц был равен 87 с^-1, а по истечении времени t=1 сут поток Ф₂ оказался равным 22 с^-1. Определить период полураспада T_1/2 изотопа.

41.18. Определить активность A фосфора ³²Р массой m=1 мг.

41.19. Вычислить удельную активность а кобальта ⁶⁰Со.

41.20. Найти отношение массовой активности a₁ стронция ⁹⁰Sr к массовой активности a₂ радия ²²⁶Ra.

41.21. Найти массу m₁ урана ²³⁸U, имеющего такую же актив­ность A, как стронций ⁹⁰Sr массой m₂=мг.

41.22. Определить массу m₂ радона ²²²Rn, находящегося в радиоактивном равновесии с радием ²²⁶Ra массой m₁=l г.

41.23. Уран ²³⁴U является продуктом распада наиболее распро­страненного изотопа урана ²³⁸U. Определить период полураспада T_1/2 урана ²³⁴U, если его массовая доля  в естественном уране ²³⁸U равна 6*10^-5.

41.24. Радиоактивный изотоп ²²₁₁Na излучает γ-кванты энергией ε=1,28МэВ. Определить мощность Р гамма-излучения и энергию W, излучаемую за время t=5 мин изотопом натрия массой m=5 г. Считать, что при каждом акте распада излучается один γ-фотон с указанной энергией.

41.25. Точечный изотропный радиоактивный источник создает на расстоянии r = 1м интенсивность I гамма-излучения, равную 1,6 мВт/м² Принимая, что при каждом акте распада ядра излу­чается один γ-фотон с энергией ε =1,33 МэВ, определить активность А источника.

41.26. Определить интенсивность I гамма-излучения на расстоя­нии r = 5 см от точечного изотропного радиоактивного источника, имеющего активность A =148 ГБк Считать, что при каждом акте распада излучается в среднем n =1,8 γ-фотонов с энергией ε = 0,51 МэВ каждый.

386