
Динамика вращательного движения
ФОРМУЛЫ
Равномерное движение по окружности:
 ;
;
 ;
;
 ;
;
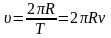 ;
;
 ;
S=φR;
;
S=φR;
 ;
;
 ;
;
 ,
,
здесь ν – частота (количество оборотов за 1 секунду), N – количество оборотов, t – время вращения, T – период обращения (время одного полного оборота), υ – скорость движения по окружности, R – радиус окружности, ω – циклическая частота или угловая скорость вращения, φ – угол поворота, aτ – тангенциальное ускорение; aцс (an) – центростремительное ускорение или нормальное ускорение, ε – угловое ускорение.
Кинематическое уравнение равномерного вращения (ω=const):
 ,
,
Кинематическое уравнение равнопеременного вращения (ε=const):
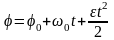 ,
,
здесь φ0 – начальное угловое перемещение, ω0 – начальная угловая скорость.
Момент инерции относительно оси вращения материальной точки:
 ,
,
здесь m – масса материальной точки, r – расстояние от оси вращения до материальной точки;
Момент инерции относительно оси вращения системы материальных точек:
 ,
,
здесь mi – масса i-й элементарной точки, ri – расстояние от материальной точки до оси вращения;
Момент инерции относительно оси вращения твердого тела:
 ,
,
здесь ρ – плотность тела;
Момент инерции некоторых тел правильной геометрической формы:
Однородный тонкий стержень массой m и длиной ℓ, ось проходит перпендикулярно стержню через центр стержня, через его край, соответственно:

Тонкое кольцо, обруч, труба массой m и радиусом R, ось проходит перпендикулярно плоскости тела через центр:
 ,
,
Круглый однородный диск массой m и радиусом R, ось проходит перпендикулярно плоскости диска через центр:
 ,
,
Однородный шар массой m и радиусом R, ось проходит через центр шара:
 ,
,
Однородная сфера массой m и радиусом R, ось проходит через центр сферы:
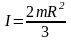 ;
;
Для плоских фигур:
 ,
,
здесь Iz – момент инерции плоской фигуры относительно оси Oz, перпендикулярной плоскости; Ix и Iy – момент инерции той же фигуры относительно осей Ox и Oy, лежащих в плоскости;
Теорема Штейнера:
 ,
,
здесь I – момент инерции тела относительно произвольной оси, I0 – момент инерции тела относительно оси, проходящей через центр тяжести тела параллельно заданной оси, ℓ – расстояние между осями, m – масса тела;
Момент силы F, действующей на тело, относительно оси вращения:
 ,
,
здесь r – радиусвектор, направленный от оси вращения к точке приложения силы F, ℓ – плечо силы (кратчайшее расстояние от оси вращения до линии действия силы, α – угол между радиусвектором и силой;
Момент импульса вращающегося тела относительно оси:
 ;
;
Закон сохранения момента импульса
 ;
;
Основное уравнение динамики вращательного движения твердого тела относительно неподвижной оси:
 ;
;
Работа момента силы, действующего на вращающееся тело:
 ,
,
здесь φ – угол поворота тела;
Кинетическая энергия вращающегося тела:
 ,
,
Кинетическая энергия тела, катящегося по плоскости:
 .
.
01.03.01. Момент инерции.
Уровень 1.
Определить момент инерции J материальной точки массой m=0,3 кг относительно оси, отстоящей от точки на r=20 см. Полученный ответ умножьте на 1000. [12]
Два маленьких шарика массой m=10 г каждый скреплены тонким невесомым стержнем длиной ℓ=20 см. Определить момент инерции J системы относительно оси, перпендикулярной стержню и проходящей через центр масс. Полученный ответ умножьте на 104. [2]
Д ва
шара массами m
и 2m
(m=10
г) закреплены на тонком невесомом стержне
длиной ℓ=40
см так, как это указано на рис. 3.7а,
б.
Определить моменты инерции J
системы относительно оси, перпендикулярной
стержню и проходящей через его конец в
этих двух случаях. Размерами шаров
пренебречь. Полученный ответ умножьте
на 104.
[36] [24]
ва
шара массами m
и 2m
(m=10
г) закреплены на тонком невесомом стержне
длиной ℓ=40
см так, как это указано на рис. 3.7а,
б.
Определить моменты инерции J
системы относительно оси, перпендикулярной
стержню и проходящей через его конец в
этих двух случаях. Размерами шаров
пренебречь. Полученный ответ умножьте
на 104.
[36] [24]
Определить момент инерции J тонкого однородного стержня длиной ℓ=30 см и массой m=100 г Относительно оси, перпендикулярной стержню и проходящей через: 1) его конец; 2) его середину; 3) (2) точку, отстоящую от конца стержня на 1/3 его длины. Полученный ответ умножьте на 105.
[300]
[75]
[100]
Найти момент инерции J тонкого однородного кольца радиусом R=20 см и массой m=100 г относительно оси, лежащей в плоскости кольца и проходящей через его центр. Полученный ответ умножьте на 1000, и округлите до целого значения. [2]
Найти момент инерции J плоской однородной прямоугольной пластины массой m=600 г относительно оси, совпадающей с одной из ее сторон, если длина a другой стороны равна 40 см. Полученный ответ умножьте на 1000. [32]
Уровень 2.
Определить момент инерции J тонкого однородного стержня длиной ℓ=30 см и массой m=100 г Относительно оси, перпендикулярной стержню и проходящей через точку, отстоящую от конца стержня на 1/3 его длины. Полученный ответ умножьте на 105. [100]
Три маленьких шарика массой m=10 г каждый расположены в вершинах равностороннего треугольника со стороной a=20 см и скреплены между собой. Определить момент инерции J системы относительно оси: 1) перпендикулярной плоскости треугольника и проходящей через центр описанной окружности; 2) лежащей в плоскости треугольника и проходящей через центр описанной окружности и одну из вершин треугольника. Массой стержней, соединяющих шары, пренебречь. Полученный ответ умножьте на 104. [4] [2]
Определить момент инерции J тонкого однородного стержня длиной ℓ=60 см и массой m=100 г относительно оси, перпендикулярной ему и проходящей через точку стержня, удаленную на a=20 см от одного из его концов. Полученный ответ умножьте на 1000. [4]
Д ва
однородных тонких стержня: АВ
длиной ℓ1=40
см и массой m1=900
г и CD
длиной ℓ2=30
см и массой m2=400
г скреплены под прямым углом (рис. 3.9).
Определить момент инерции J
системы стержней относительно оси OOʹ,
проходящей через конец стержня АВ
параллельно стержню CD.
Полученный ответ умножьте на 1000. [112]
ва
однородных тонких стержня: АВ
длиной ℓ1=40
см и массой m1=900
г и CD
длиной ℓ2=30
см и массой m2=400
г скреплены под прямым углом (рис. 3.9).
Определить момент инерции J
системы стержней относительно оси OOʹ,
проходящей через конец стержня АВ
параллельно стержню CD.
Полученный ответ умножьте на 1000. [112]
Определить момент инерции J кольца массой m=200 г и радиусом R=10 см относительно оси, касательной к кольцу. Полученный ответ умножьте на 1000. [3]
Диаметр диска d=20 см, масса m=800 г. Определить момент инерции J диска относительно оси, проходящей через середину одного из радиусов перпендикулярно плоскости диска. Полученный ответ умножьте на 1000. [6]
Определить момент инерции J тонной плоской пластины со сторонами a=10 см и b=20 см относительно оси, проходящей через центр масс пластины параллельно большей стороне. Масса пластины равномерно распределена по ее площади с поверхностной плотностью σ=1,2 кг/м2. Полученный ответ умножьте на 1000. [200]
Уровень 3.
Д ва однородных тонких стержня: АВ длиной ℓ1=40 см и массой m1=900 г и CD длиной ℓ2=30 см и массой m2=400 г скреплены под прямым углом (рис. 3.9). Определить момент инерции J системы стержней относительно оси OOʹ, проходящей через точку A перпендикулярно плоскости чертежа. Полученный ответ умножьте на 1000. [115]
(3) 1. Момент инерции.
О пределить
моменты инерции Jx,
Jy,
Jz
трехатомных молекул типа AB2
относительно осей x,
у,
z
(рис. 3.8), проходящих через центр инерции
C
молекулы (ось z
перпендикулярна плоскости xy).
Межъядерное расстояние AB
обозначено d,
валентный угол α. Вычисления выполнить
для следующих молекул: 1) Н2О
(d=0,097
нм, α=104º30'); 2) SO2
(d=0,145
нм, α=124º). m(O)=26,552·10-27
кг, m(H)=1,673·10-27
кг,
m(S)=53,220·10-27
кг. Полученный ответ умножьте на 1050,
и округлите до целого значения.
пределить
моменты инерции Jx,
Jy,
Jz
трехатомных молекул типа AB2
относительно осей x,
у,
z
(рис. 3.8), проходящих через центр инерции
C
молекулы (ось z
перпендикулярна плоскости xy).
Межъядерное расстояние AB
обозначено d,
валентный угол α. Вычисления выполнить
для следующих молекул: 1) Н2О
(d=0,097
нм, α=104º30'); 2) SO2
(d=0,145
нм, α=124º). m(O)=26,552·10-27
кг, m(H)=1,673·10-27
кг,
m(S)=53,220·10-27
кг. Полученный ответ умножьте на 1050,
и округлите до целого значения.
1) (3) [1048] [1047]
(2) [1968] [1969]
(4) [3016] [3017]
2) (3) [12081] [12080]
(2) [83765] [83764]
(4) [95844] [95845]
Вычислить момент инерции J проволочного прямоугольника со сторонами a=12 см и b=16 см относительно оси, лежащей в плоскости прямоугольника и проходящей через середины малых сторон. Масса равномерно распределена по длине проволоки с линейной плотностью τ=0,1 кг/м. Полученный ответ умножьте на 106. [144]
О пределить
момент инерции J
проволочного равностороннего треугольника
со стороной a=10
см относительно: 1) оси, лежащей в плоскости
треугольника и проходящей через его
вершину параллельно стороне, противоположной
этой вершине (рис. 3.10а);
2) оси, совпадающей с одной из сторон
треугольника (рис. 3. 10б).
Масса m
треугольника равна 12 г и равномерно
распределена по длине, проволоки.
Полученный ответ умножьте на 105.
[5] [2]
пределить
момент инерции J
проволочного равностороннего треугольника
со стороной a=10
см относительно: 1) оси, лежащей в плоскости
треугольника и проходящей через его
вершину параллельно стороне, противоположной
этой вершине (рис. 3.10а);
2) оси, совпадающей с одной из сторон
треугольника (рис. 3. 10б).
Масса m
треугольника равна 12 г и равномерно
распределена по длине, проволоки.
Полученный ответ умножьте на 105.
[5] [2]
Н
 а
концах тонкого однородного стержня
длиной ℓ
и массой 3m
прикреплены маленькие шарики массами
m
и 2m.
Определить момент инерции J
такой системы относительно оси,
перпендикулярной стержню и проходящей
через точку O,
лежащую на оси стержня. Вычисления
выполнить для случаев x=0(2),
ℓ/3,
ℓ/2,
2ℓ/3,
ℓ
(см. рис. 3.11). При расчетах принять ℓ=1
м, m=3
кг. Шарики рассматривать как материальные
точки. [9]
[4]
[3] [3] [6]
а
концах тонкого однородного стержня
длиной ℓ
и массой 3m
прикреплены маленькие шарики массами
m
и 2m.
Определить момент инерции J
такой системы относительно оси,
перпендикулярной стержню и проходящей
через точку O,
лежащую на оси стержня. Вычисления
выполнить для случаев x=0(2),
ℓ/3,
ℓ/2,
2ℓ/3,
ℓ
(см. рис. 3.11). При расчетах принять ℓ=1
м, m=3
кг. Шарики рассматривать как материальные
точки. [9]
[4]
[3] [3] [6]
В однородном диске массой m=18 кг и радиусом r=30 см вырезано круглое, отверстие диаметром d=20 см, центр которого находится на расстоянии ℓ=15 см от оси диска (рис. 3.12). Найти момент инерции J полученного тела относительно оси, проходящей перпендикулярно плоскости диска через его центр. Полученный ответ умножьте на 1000. [755]
Уровень 4.
Уровень 5. Интегрирование.
